华东师大版八年级下册数学17.3.2直线的平移课件 (共26张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学17.3.2直线的平移课件 (共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 23:15:51 | ||
图片预览







文档简介
(共26张PPT)
17.3.2直线的平移
华东师范大学出版社
八年级下册
每天告诉自己一次:
“我真的很不错”。
你能找到它们的共同特征吗?
各抒己见
在生活中,你知道哪些平移的例子?
平面图形在它所在的平面上的平行移动,简称为平移。
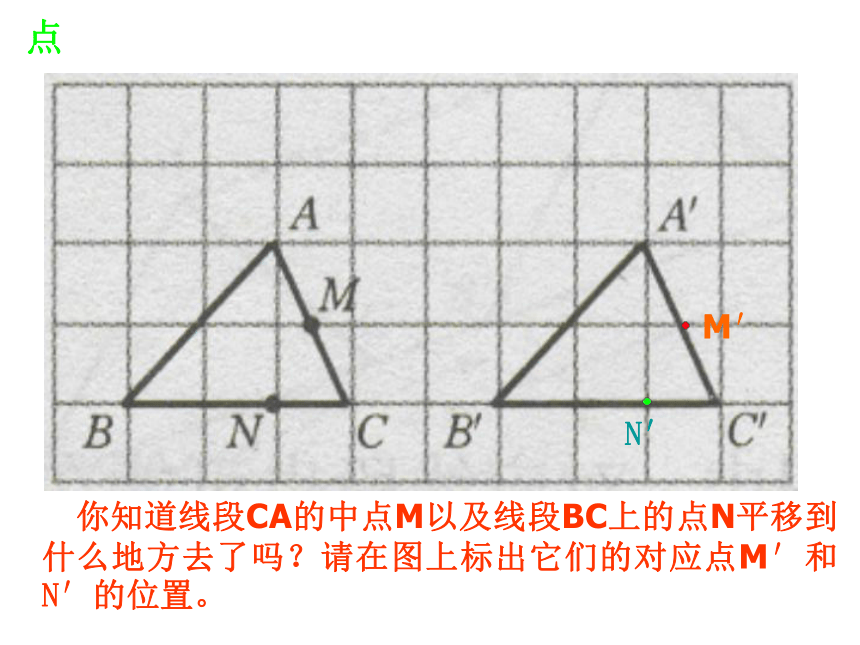
你知道线段CA的中点M以及线段BC上的点N平移到什么地方去了吗?请在图上标出它们的对应点M′和N′的位置。
M′
N′
点
A
A′
B
C
图形
B′
C′
平移方格纸中的图形,使点A平移到A′处,画出平移后的图形
1.一次函数的图象是什么图形?
2.直线y=kx+b与x轴的交点坐标是
(
),与y轴的交点坐标(
).
一条直线
0,
b
回顾
思考
-3
-2
-4
-1
0
-1
-2
-3
1
2
?
3
4
1
2
3
4
?
?
?
5
y=2x
-4
?
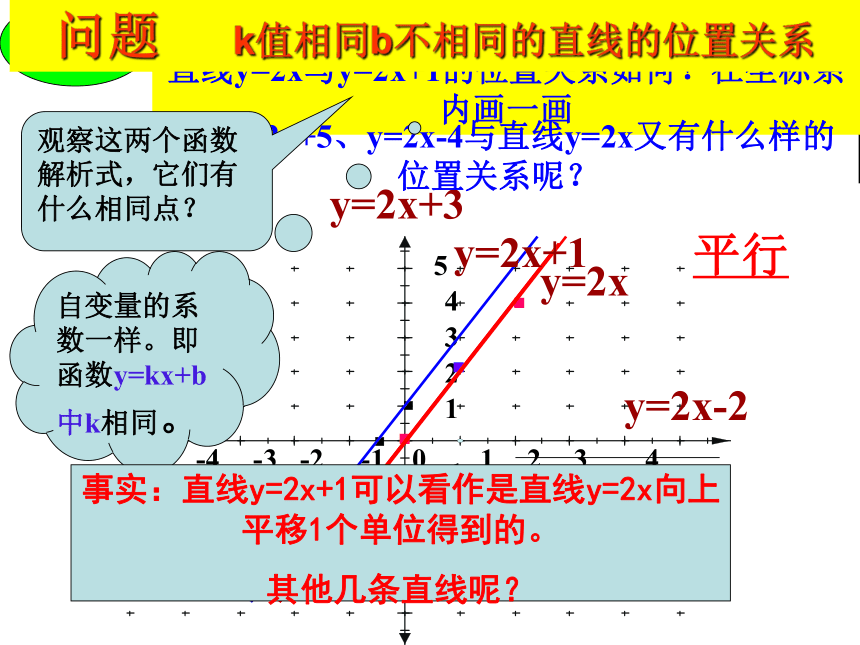
直线y=2x与y=2x+1的位置关系如何?在坐标系内画一画
■
■
y=2x+3
平行
直线y=2x+5、y=2x-4与直线y=2x又有什么样的位置关系呢?
y=2x-2
y=2x+1
观察这两个函数解析式,它们有什么相同点?
自变量的系数一样。即函数y=kx+b中k相同。
事实:直线y=2x+1可以看作是直线y=2x向上平移1个单位得到的。
其他几条直线呢?
问题
k值相同b不相同的直线的位置关系
y
-4
-2
-3
-1
3
2
1
-1
0
-2
1
2
3
4
5
x
-5
y=2x
y=2x+3
y=2x-2
y=2x+0
y=2x+3
y=2x
--2
(0,0)
(1,2)
(0,3)
(1,5)
(0,-2)
(1,0)
例1.
在同一坐标系内作出下列函数
y=2x,
y=2x+3,y=2x-2的图象。
2
2
k相等
平行
1.直线y=2x过
(0,0).
(0,3)
3
(0,-2)
2
上
下
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
直线y=kx+b可以看作直线y=kx向上(或向下)平移
|b|
个单位长度得到的
当b<0时,向下平移
当b>0时,向上平移
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
1.将直线y=1/2x向下平移2个单位得到直线_____________。
y=1/2x-2
3.将直线y=-x-5向上平移5个单位,得到直线____________。
y=-x
2
.将直线y=-2x向上平移4个单位,得到直线,则其函数的表达式为______________。
y=
-2x
+4
4
.将直线y=3x+3向下平移5个单
位长度得到直线为________。.
y=3x-2
小结
一次函数的k值相等时,它们的图象互相平行。
直线y=kx+b可以看作是直线y=kx上下平移
∣
b∣个单位得到的。
当b<0时,直线y=kx
向下平移∣
b∣个单位得到直线y=kx+b
;
当b
>0时,直线y=kx
向上平移∣
b∣个单位得到直线y=kx+b
。
常数项
(上加下减)
直线y=kx+b,
平移后斜率不变,所以平移后函数可写为
y=kx+c
则其与y轴交点为(0,b)。
1.
向上移n则与y轴交点为(0,b+n),将平移后的点代入方程得
b+n=k
0+c
=>
c=b+n
所以上移n后函数为:
y=kx+b+n
2.
向下移n则与y轴交点为(0,b-n),将平移后的点代入方程得
b-n=k
0+c
=>
c=b-n
所以下移n后函数为:
y=kx+b-n
能力提升
y
-4
-2
-3
-1
3
2
1
-1
0
-2
1
2
3
4
5
x
-5
y=2x
y=2x+4
y=2x-2
y=2(x+0)=2x
y=2(x+2)=2x+4
y=2(x
-1)=2x--2
(2,4)
(o,4)
(3,4)
例2.
在同一坐标系内作出下列函数
y=2x,
y=2x+4,y=2x-2的图象。
2
k相等
平行
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
1.直线y=2x+4
=2(x+2)
它是由直线y=2x
=2(x+0)向
左
平移
2
个单位长度得到。
练习
1.当函数y=2x向右平移3个单位时,得到的函数解析式是______
2.当函数y=4x向左平移1个单位时,得到的函数解析式是_____y=4x+4
y=2x-6
你能自己总结出向右平移或向左平移后解析式变化的规律吗?试一试
小结:直线y=k(x+
h)可以看作是
由直线y=kx向左(或向右)平移
|h|
个单位长度得到。
平移规律:自变量
左加右减
3.当函数y=2x+1向右平移2个单位时,得到
的函数解析式是______
y=2x-3
一次函数y=kx+b平移的规律:y=kx+c
左加右减
1.
向左移n则与x轴交点为(-b/k
-n,0),将改点代入方程得
0=k(-b/k-n)+c
=>c=b+kn
所以左移n后函数为:
y=kx+b+kn=k(x+n)+b
2.
向右移n则与x轴交点为(-b/k+n,0),将改点代入方程得
0=k(-b/k+n)+c
=>c=b-kn
所以右移n后函数为:
y=kx+b-kn=k(x-n)+b
能力提升
总结
1.直线y=kx+b可以看作直线y=kx向上(或向下)平移
|b|
个单位长度得到的
这节课你都学到了什么?
2.当函数y=kx+b向左(右)平移︱h︱个单
位时,得到的函数解析式是_
y=k(x+
h)+b
_____
作业:
1.直线y=2x怎样平移,平移多少个单位才能可得到直线y=2x+3。
你能从哪些角度理解自己的答案?
一:作直观图
(数形结合)
二:解方程
2.同步练习册相应练习
新龟兔赛跑
乌龟
兔
y
(米)
1
2
3
4
5
O
100
20
120
40
60
80
x(分)
6
8
7
(1)乌龟说:“你站在起点上,我站在你前面40米,我们仍然保持第一次比赛的速度,那么我们将会同时到达,不信咱俩试试看.”你觉得乌龟分析的对吗?为什么?
-1
12
9
10
11
-3
-2
-4
下图
l1
、l2
分别是乌龟和兔子赛跑中路程与时间之间的函数图象.
根据图象回答问题:
l1
l2
y
(米)
1
2
3
4
5
O
100
20
120
40
60
80
x
(分)
6
8
7
-1
12
9
10
11
-3
-2
-4
-20
-
40
-
60
(2)兔子很郁闷,分析之后又对乌龟说:“你在起点上,我往后退40m,我们再来比一次!”你觉得他们还会同时到达吗?为什么?
l1
l2
y(米)
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
x
(分)
6
8
7
-1
12
9
10
11
-3
-2
-4
-20
-
40
-
60
(3)想一想:兔子要后退多少米,兔子与乌龟才会同时到达?
17.3.2直线的平移
华东师范大学出版社
八年级下册
每天告诉自己一次:
“我真的很不错”。
你能找到它们的共同特征吗?
各抒己见
在生活中,你知道哪些平移的例子?
平面图形在它所在的平面上的平行移动,简称为平移。
你知道线段CA的中点M以及线段BC上的点N平移到什么地方去了吗?请在图上标出它们的对应点M′和N′的位置。
M′
N′
点
A
A′
B
C
图形
B′
C′
平移方格纸中的图形,使点A平移到A′处,画出平移后的图形
1.一次函数的图象是什么图形?
2.直线y=kx+b与x轴的交点坐标是
(
),与y轴的交点坐标(
).
一条直线
0,
b
回顾
思考
-3
-2
-4
-1
0
-1
-2
-3
1
2
?
3
4
1
2
3
4
?
?
?
5
y=2x
-4
?
直线y=2x与y=2x+1的位置关系如何?在坐标系内画一画
■
■
y=2x+3
平行
直线y=2x+5、y=2x-4与直线y=2x又有什么样的位置关系呢?
y=2x-2
y=2x+1
观察这两个函数解析式,它们有什么相同点?
自变量的系数一样。即函数y=kx+b中k相同。
事实:直线y=2x+1可以看作是直线y=2x向上平移1个单位得到的。
其他几条直线呢?
问题
k值相同b不相同的直线的位置关系
y
-4
-2
-3
-1
3
2
1
-1
0
-2
1
2
3
4
5
x
-5
y=2x
y=2x+3
y=2x-2
y=2x+0
y=2x+3
y=2x
--2
(0,0)
(1,2)
(0,3)
(1,5)
(0,-2)
(1,0)
例1.
在同一坐标系内作出下列函数
y=2x,
y=2x+3,y=2x-2的图象。
2
2
k相等
平行
1.直线y=2x过
(0,0).
(0,3)
3
(0,-2)
2
上
下
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
直线y=kx+b可以看作直线y=kx向上(或向下)平移
|b|
个单位长度得到的
当b<0时,向下平移
当b>0时,向上平移
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
1.将直线y=1/2x向下平移2个单位得到直线_____________。
y=1/2x-2
3.将直线y=-x-5向上平移5个单位,得到直线____________。
y=-x
2
.将直线y=-2x向上平移4个单位,得到直线,则其函数的表达式为______________。
y=
-2x
+4
4
.将直线y=3x+3向下平移5个单
位长度得到直线为________。.
y=3x-2
小结
一次函数的k值相等时,它们的图象互相平行。
直线y=kx+b可以看作是直线y=kx上下平移
∣
b∣个单位得到的。
当b<0时,直线y=kx
向下平移∣
b∣个单位得到直线y=kx+b
;
当b
>0时,直线y=kx
向上平移∣
b∣个单位得到直线y=kx+b
。
常数项
(上加下减)
直线y=kx+b,
平移后斜率不变,所以平移后函数可写为
y=kx+c
则其与y轴交点为(0,b)。
1.
向上移n则与y轴交点为(0,b+n),将平移后的点代入方程得
b+n=k
0+c
=>
c=b+n
所以上移n后函数为:
y=kx+b+n
2.
向下移n则与y轴交点为(0,b-n),将平移后的点代入方程得
b-n=k
0+c
=>
c=b-n
所以下移n后函数为:
y=kx+b-n
能力提升
y
-4
-2
-3
-1
3
2
1
-1
0
-2
1
2
3
4
5
x
-5
y=2x
y=2x+4
y=2x-2
y=2(x+0)=2x
y=2(x+2)=2x+4
y=2(x
-1)=2x--2
(2,4)
(o,4)
(3,4)
例2.
在同一坐标系内作出下列函数
y=2x,
y=2x+4,y=2x-2的图象。
2
k相等
平行
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
1.直线y=2x+4
=2(x+2)
它是由直线y=2x
=2(x+0)向
左
平移
2
个单位长度得到。
练习
1.当函数y=2x向右平移3个单位时,得到的函数解析式是______
2.当函数y=4x向左平移1个单位时,得到的函数解析式是_____y=4x+4
y=2x-6
你能自己总结出向右平移或向左平移后解析式变化的规律吗?试一试
小结:直线y=k(x+
h)可以看作是
由直线y=kx向左(或向右)平移
|h|
个单位长度得到。
平移规律:自变量
左加右减
3.当函数y=2x+1向右平移2个单位时,得到
的函数解析式是______
y=2x-3
一次函数y=kx+b平移的规律:y=kx+c
左加右减
1.
向左移n则与x轴交点为(-b/k
-n,0),将改点代入方程得
0=k(-b/k-n)+c
=>c=b+kn
所以左移n后函数为:
y=kx+b+kn=k(x+n)+b
2.
向右移n则与x轴交点为(-b/k+n,0),将改点代入方程得
0=k(-b/k+n)+c
=>c=b-kn
所以右移n后函数为:
y=kx+b-kn=k(x-n)+b
能力提升
总结
1.直线y=kx+b可以看作直线y=kx向上(或向下)平移
|b|
个单位长度得到的
这节课你都学到了什么?
2.当函数y=kx+b向左(右)平移︱h︱个单
位时,得到的函数解析式是_
y=k(x+
h)+b
_____
作业:
1.直线y=2x怎样平移,平移多少个单位才能可得到直线y=2x+3。
你能从哪些角度理解自己的答案?
一:作直观图
(数形结合)
二:解方程
2.同步练习册相应练习
新龟兔赛跑
乌龟
兔
y
(米)
1
2
3
4
5
O
100
20
120
40
60
80
x(分)
6
8
7
(1)乌龟说:“你站在起点上,我站在你前面40米,我们仍然保持第一次比赛的速度,那么我们将会同时到达,不信咱俩试试看.”你觉得乌龟分析的对吗?为什么?
-1
12
9
10
11
-3
-2
-4
下图
l1
、l2
分别是乌龟和兔子赛跑中路程与时间之间的函数图象.
根据图象回答问题:
l1
l2
y
(米)
1
2
3
4
5
O
100
20
120
40
60
80
x
(分)
6
8
7
-1
12
9
10
11
-3
-2
-4
-20
-
40
-
60
(2)兔子很郁闷,分析之后又对乌龟说:“你在起点上,我往后退40m,我们再来比一次!”你觉得他们还会同时到达吗?为什么?
l1
l2
y(米)
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
x
(分)
6
8
7
-1
12
9
10
11
-3
-2
-4
-20
-
40
-
60
(3)想一想:兔子要后退多少米,兔子与乌龟才会同时到达?
