人教版2020年春数学九年级下册29.2 三视图(1)(WPS打开,共27张PPT)
文档属性
| 名称 | 人教版2020年春数学九年级下册29.2 三视图(1)(WPS打开,共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
三视图
29.2
三视图
人教版数学九年级下册
1.
能从投影的角度理解视图的概念,明确视图与投影的关系.
2.能识别物体的三视图,会画简单几何体的三视图.
学习目标
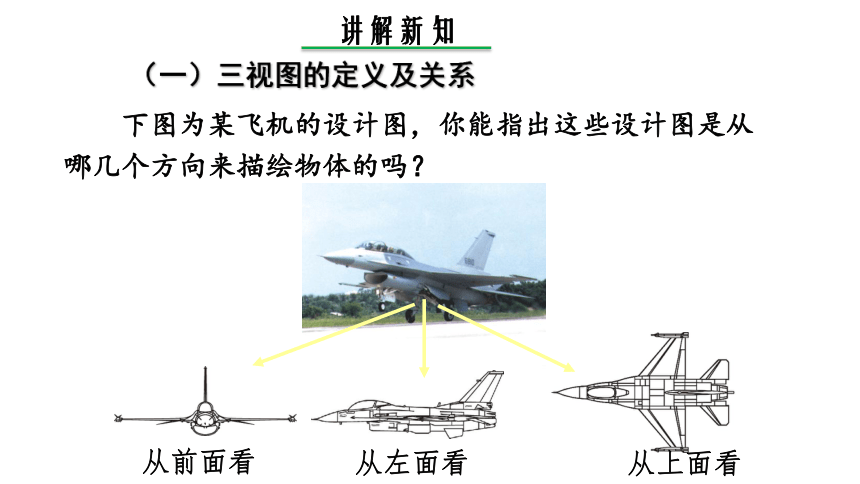
下图为某飞机的设计图,你能指出这些设计图是从哪几个方向来描绘物体的吗?
(一)三视图的定义及关系
从前面看
从左面看
从上面看
讲解新知
请你从前、后、左、右、上、下六个方向观察同一本字典,画出得到的正投影,你有什么发现?
1.
前面和后面正投影
的形状、大小一致;
2.
上面和下面正投影
的形状、大小一致;
3.
左面和右面正投影
的形状、大小一致;
当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图.视图也可以看作物体在某一方向光线下的正投影,对于同一个物体,如果从不同方向观察,所得到的视图可能不同.
归纳新知
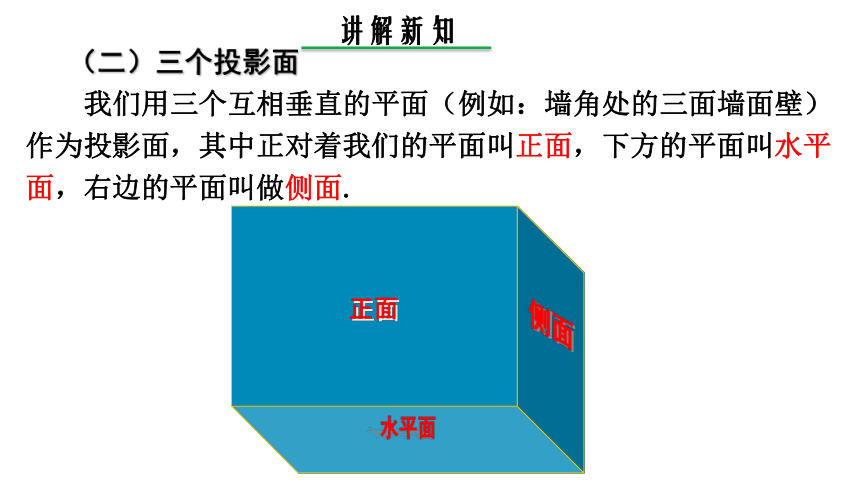
正面
侧面
水平面
(二)三个投影面
我们用三个互相垂直的平面(例如:墙角处的三面墙面壁)作为投影面,其中正对着我们的平面叫正面,下方的平面叫水平面,右边的平面叫做侧面.
讲解新知
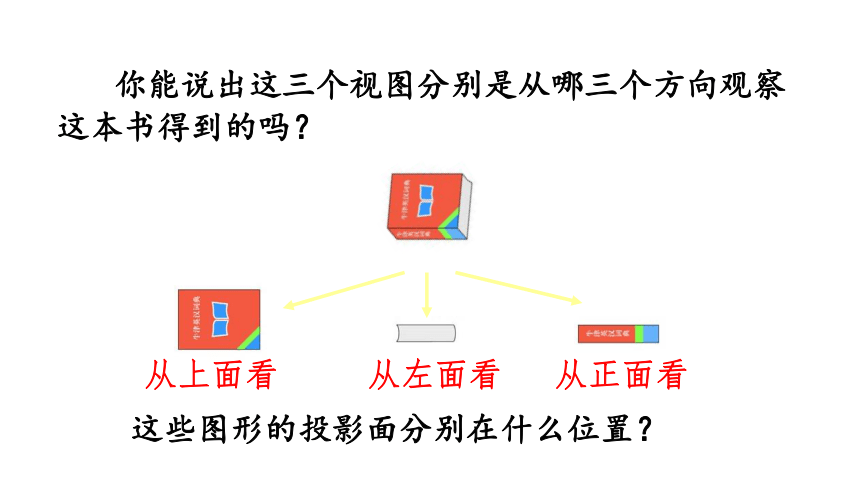
你能说出这三个视图分别是从哪三个方向观察这本书得到的吗?
从上面看
从左面看
从正面看
这些图形的投影面分别在什么位置?
U
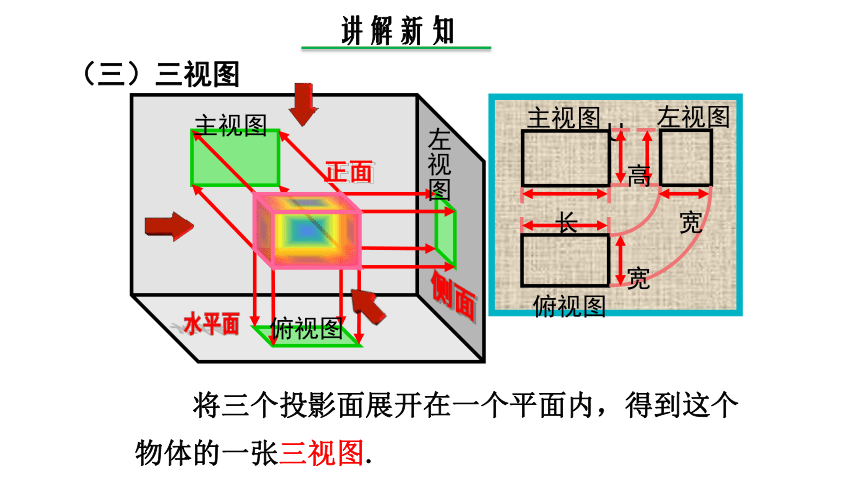
主视图
主视图
俯视图
左视图
正面
高
长
宽
宽
(三)三视图
侧面
水平面
俯视图
左视图
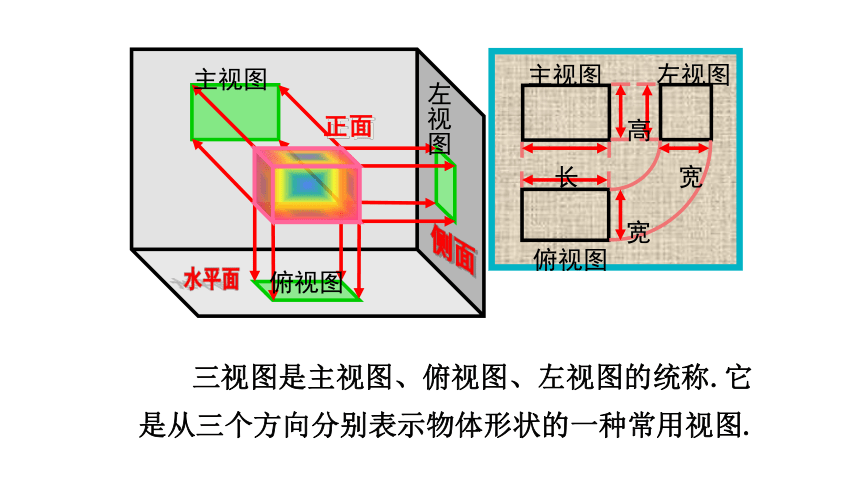
将三个投影面展开在一个平面内,得到这个物体的一张三视图.
讲解新知
三视图是主视图、俯视图、左视图的统称.它是从三个方向分别表示物体形状的一种常用视图.
主视图
主视图
俯视图
左视图
正面
高
长
宽
宽
侧面
水平面
俯视图
左视图
对一个物体在三个投影面内进行正投影,
在正面内得到的由前向后观察物体的视图,叫做主视图;
在水平面内得到的由上向下观察物体的视图,叫做俯视图;
在侧面内得到的由左向右观察物体的视图,叫做左视图.
归纳新知
例1
画出图中基本几何体的三视图:
(四)已知简单几何体画三视图
圆柱(1)
正三棱柱
(2)
球
(3)
讲解新知
主视图
宽
左视图
解:如图所示:
俯视图
主视图
左视图
俯视图
圆柱(1)
正三棱柱
(2)
球
(3)
3.
在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;
1.
确定主视图的位置,画出主视图;
2.
在主视图正下方画出俯视图,注
意与主视图“长对正”;
三视图的具体画法为:
主视图
俯视图
左视图
高
长
宽
宽
注:可见的轮廓线画成实线;不可见的轮廓线,画成虚线.
归纳:
4.
为表示圆柱、圆锥等的对称轴,规定在视图中加画点划线(
)表示对称轴.
1.
画出半球和圆锥的三视图.
半球
主视图
俯视图
左视图
圆锥
主视图
俯视图
左视图
·
巩固练习
例2
画出如图所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
解:下图是支架的三视图.
主视图
俯视图
左视图
(五)已知较复杂几何体画三视图
提示:长对正,高平齐,宽相等,不可见的轮廓线,用虚线画出.
讲解新知
2.如图是两个等直径圆柱构成的“T”形管道,其左视图是( )
A.
B.
C.
D.
B
巩固练习
例3
画出该几何体的三视图.
(六)作几何组合体的三视图
分析:这是一个圆柱体的组合体,从不同角度看它时,会呈现不同的视图,为全面地反映立体图形的现状,画图时规定:
看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
讲解新知
主视图
左视图
俯视图
解:下图是组合体的三视图.
3.画出图中简单组合体的三视图:
主视图
左视图
俯视图
解:三视图如下:
巩固练习
1.下列立体图形中,主视图是三角形的是( )
A.
B.
C.
D.
B
2.一个几何体的三视图形状都相同,大小均等,那么这个几何体不可以是(
)
A.球
B.正三棱锥
C.正方体
D.圆柱
D
课堂检测
3.将矩形硬纸板绕它的一条边旋转180°所形成的几何体的主视图和俯视图不可能是(
)
A.矩形,矩形
B.半圆、矩形
C.圆、矩形
D.矩形、半圆
C
4.下图中①表示的是组合在一起的模块,那么这个
模块的俯视图是(
)
A.②
B.③
C.④
D.⑤
A
①
②
③
④
⑤
俯视图
(
)
左视图
(
)
主视图
(
)
A
B
C
A
A
B
5.找出对应的三视图.
6.画出图中的几何体的三视图.
解:如图所示:
7.图是一根钢管的直观图,画出它的三视图.
解:钢管的三视图为:
主视图
俯视图
左视图
三视图
三视图的概念及关系
三视图的画法
简单几何体的三视图
总结新知
三视图
29.2
三视图
人教版数学九年级下册
1.
能从投影的角度理解视图的概念,明确视图与投影的关系.
2.能识别物体的三视图,会画简单几何体的三视图.
学习目标
下图为某飞机的设计图,你能指出这些设计图是从哪几个方向来描绘物体的吗?
(一)三视图的定义及关系
从前面看
从左面看
从上面看
讲解新知
请你从前、后、左、右、上、下六个方向观察同一本字典,画出得到的正投影,你有什么发现?
1.
前面和后面正投影
的形状、大小一致;
2.
上面和下面正投影
的形状、大小一致;
3.
左面和右面正投影
的形状、大小一致;
当我们从某一方向观察一个物体时,所看到的平面图形叫做物体的一个视图.视图也可以看作物体在某一方向光线下的正投影,对于同一个物体,如果从不同方向观察,所得到的视图可能不同.
归纳新知
正面
侧面
水平面
(二)三个投影面
我们用三个互相垂直的平面(例如:墙角处的三面墙面壁)作为投影面,其中正对着我们的平面叫正面,下方的平面叫水平面,右边的平面叫做侧面.
讲解新知
你能说出这三个视图分别是从哪三个方向观察这本书得到的吗?
从上面看
从左面看
从正面看
这些图形的投影面分别在什么位置?
U
主视图
主视图
俯视图
左视图
正面
高
长
宽
宽
(三)三视图
侧面
水平面
俯视图
左视图
将三个投影面展开在一个平面内,得到这个物体的一张三视图.
讲解新知
三视图是主视图、俯视图、左视图的统称.它是从三个方向分别表示物体形状的一种常用视图.
主视图
主视图
俯视图
左视图
正面
高
长
宽
宽
侧面
水平面
俯视图
左视图
对一个物体在三个投影面内进行正投影,
在正面内得到的由前向后观察物体的视图,叫做主视图;
在水平面内得到的由上向下观察物体的视图,叫做俯视图;
在侧面内得到的由左向右观察物体的视图,叫做左视图.
归纳新知
例1
画出图中基本几何体的三视图:
(四)已知简单几何体画三视图
圆柱(1)
正三棱柱
(2)
球
(3)
讲解新知
主视图
宽
左视图
解:如图所示:
俯视图
主视图
左视图
俯视图
圆柱(1)
正三棱柱
(2)
球
(3)
3.
在主视图正右方画出左视图,注意与主视图“高平齐”,与俯视图“宽相等”;
1.
确定主视图的位置,画出主视图;
2.
在主视图正下方画出俯视图,注
意与主视图“长对正”;
三视图的具体画法为:
主视图
俯视图
左视图
高
长
宽
宽
注:可见的轮廓线画成实线;不可见的轮廓线,画成虚线.
归纳:
4.
为表示圆柱、圆锥等的对称轴,规定在视图中加画点划线(
)表示对称轴.
1.
画出半球和圆锥的三视图.
半球
主视图
俯视图
左视图
圆锥
主视图
俯视图
左视图
·
巩固练习
例2
画出如图所示的支架(一种小零件)的三视图,其中支架的两个台阶的高度和宽度相等.
解:下图是支架的三视图.
主视图
俯视图
左视图
(五)已知较复杂几何体画三视图
提示:长对正,高平齐,宽相等,不可见的轮廓线,用虚线画出.
讲解新知
2.如图是两个等直径圆柱构成的“T”形管道,其左视图是( )
A.
B.
C.
D.
B
巩固练习
例3
画出该几何体的三视图.
(六)作几何组合体的三视图
分析:这是一个圆柱体的组合体,从不同角度看它时,会呈现不同的视图,为全面地反映立体图形的现状,画图时规定:
看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.
讲解新知
主视图
左视图
俯视图
解:下图是组合体的三视图.
3.画出图中简单组合体的三视图:
主视图
左视图
俯视图
解:三视图如下:
巩固练习
1.下列立体图形中,主视图是三角形的是( )
A.
B.
C.
D.
B
2.一个几何体的三视图形状都相同,大小均等,那么这个几何体不可以是(
)
A.球
B.正三棱锥
C.正方体
D.圆柱
D
课堂检测
3.将矩形硬纸板绕它的一条边旋转180°所形成的几何体的主视图和俯视图不可能是(
)
A.矩形,矩形
B.半圆、矩形
C.圆、矩形
D.矩形、半圆
C
4.下图中①表示的是组合在一起的模块,那么这个
模块的俯视图是(
)
A.②
B.③
C.④
D.⑤
A
①
②
③
④
⑤
俯视图
(
)
左视图
(
)
主视图
(
)
A
B
C
A
A
B
5.找出对应的三视图.
6.画出图中的几何体的三视图.
解:如图所示:
7.图是一根钢管的直观图,画出它的三视图.
解:钢管的三视图为:
主视图
俯视图
左视图
三视图
三视图的概念及关系
三视图的画法
简单几何体的三视图
总结新知
