人教版七年级数学下 7.1 平面直角坐标系 同步练习试题含答案
文档属性
| 名称 | 人教版七年级数学下 7.1 平面直角坐标系 同步练习试题含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 82.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 21:50:10 | ||
图片预览


文档简介
7.1
平面直角坐标系
一.选择题(共12小题)
1.在平面直角坐标系中,点(﹣2,3)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.下列各点中,在第三象限的点是( )
A.(﹣1,﹣4)
B.(1,﹣4)
C.(﹣1,4)
D.(1,4)
3.平面直角坐标系内,下列的点位于第四象限的是( )
A.(﹣3,1)
B.(﹣3,﹣1)
C.(3,﹣1)
D.(0,﹣1)
4.点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3)
B.(﹣5,3)
C.(3,﹣5)
D.(﹣3,5)
5.在平面直角坐标系中,点(﹣6,7)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.下列各点中,第四象限内的点是( )
A.(1,2)
B.(﹣2,﹣3)
C.(﹣2,1)
D.(1,﹣2)
7.点P(﹣3,﹣4)位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.已知点P(3a,a+2)在x轴上,则P点的坐标是( )
A.(3,2)
B.(6,0)
C.(﹣6,0)
D.(6,2)
9.已知点P(a,b)在第四象限,且点P到x轴的距离为3,到y轴的距离为6,则点P的坐标是( )
A.(3,﹣6)
B.(6,﹣3)
C.(﹣3,6)
D.(﹣3,3)或(﹣6,6)
10.点M(﹣2019,2019)的位置在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
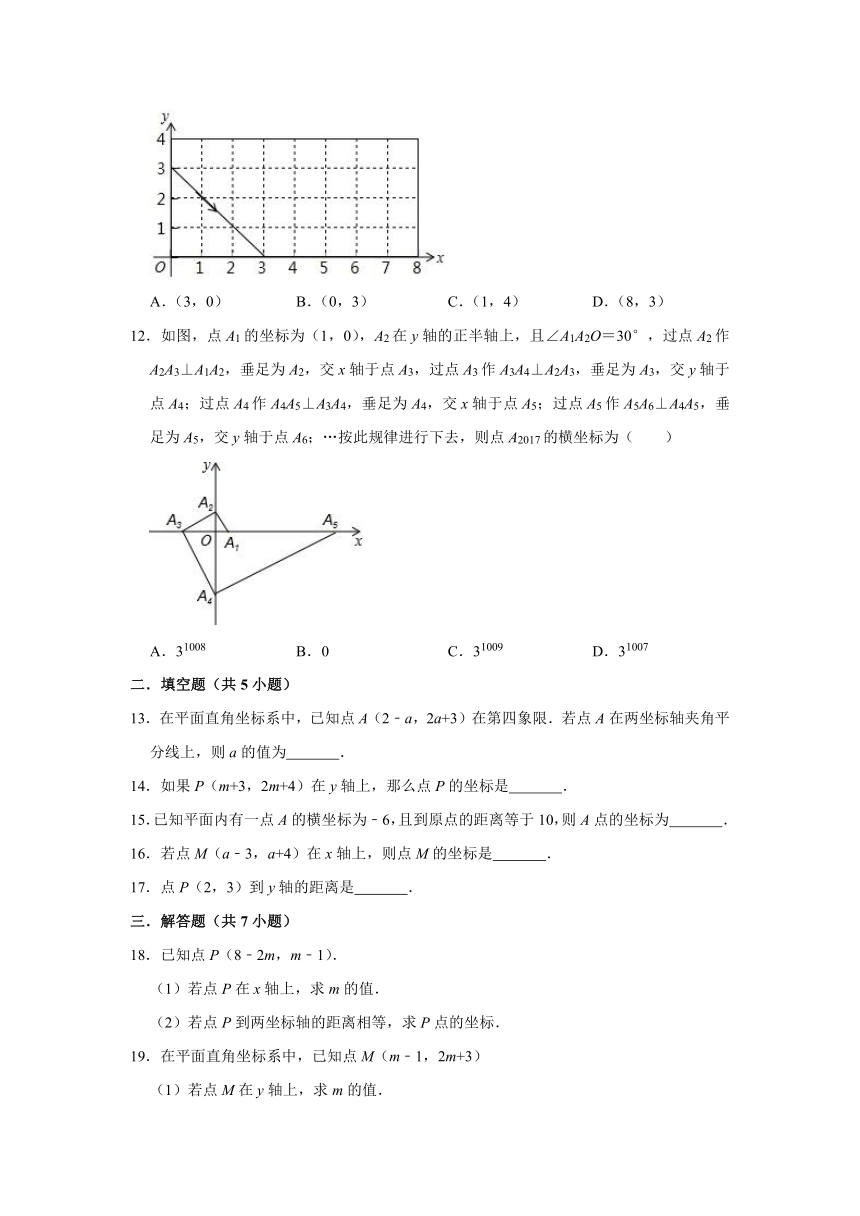
11.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2017次碰到矩形的边时,点P的坐标为( )
A.(3,0)
B.(0,3)
C.(1,4)
D.(8,3)
12.如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为( )
A.31008
B.0
C.31009
D.31007
二.填空题(共5小题)
13.在平面直角坐标系中,已知点A(2﹣a,2a+3)在第四象限.若点A在两坐标轴夹角平分线上,则a的值为
.
14.如果P(m+3,2m+4)在y轴上,那么点P的坐标是
.
15.已知平面内有一点A的横坐标为﹣6,且到原点的距离等于10,则A点的坐标为
.
16.若点M(a﹣3,a+4)在x轴上,则点M的坐标是
.
17.点P(2,3)到y轴的距离是
.
三.解答题(共7小题)
18.已知点P(8﹣2m,m﹣1).
(1)若点P在x轴上,求m的值.
(2)若点P到两坐标轴的距离相等,求P点的坐标.
19.在平面直角坐标系中,已知点M(m﹣1,2m+3)
(1)若点M在y轴上,求m的值.
(2)若点M在第一、三象限的角平分线上,求m的值.
20.在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”例如,点P(1,4)的“3级美联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)已知点A(﹣2,6)的“级关联点”是点A1,求点A1的坐标.
(2)已知点M(m﹣1,2m)的“﹣3级关联点”M′位于y轴上.求点M′的坐标.
21.如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)
22.每个小方格都是边长为1的正方形,在平面直角坐标系中.
(1)写出图中从原点O出发,按箭头所指方向先后经过的A、B、C、D、E这几个点点的坐标;
(2)按图中所示规律,找到下一个点F的位置并写出它的坐标.
23.如图,在直角坐标系的坐标轴上按如下规律取点:A1在x轴正半轴上,A2在y轴正半轴上,A3在x轴负半轴上,A4在y轴负半轴上,A5在x轴正半轴上,…,且OA1+1=OA2,OA2+1=OA3,OA3+1=OA4…,设A1,A2,A3,A4…,有坐标分别为(a1,0),(0,a2),(a3,0),(0,a4)…,sn=a1+a2+a3+…+an.
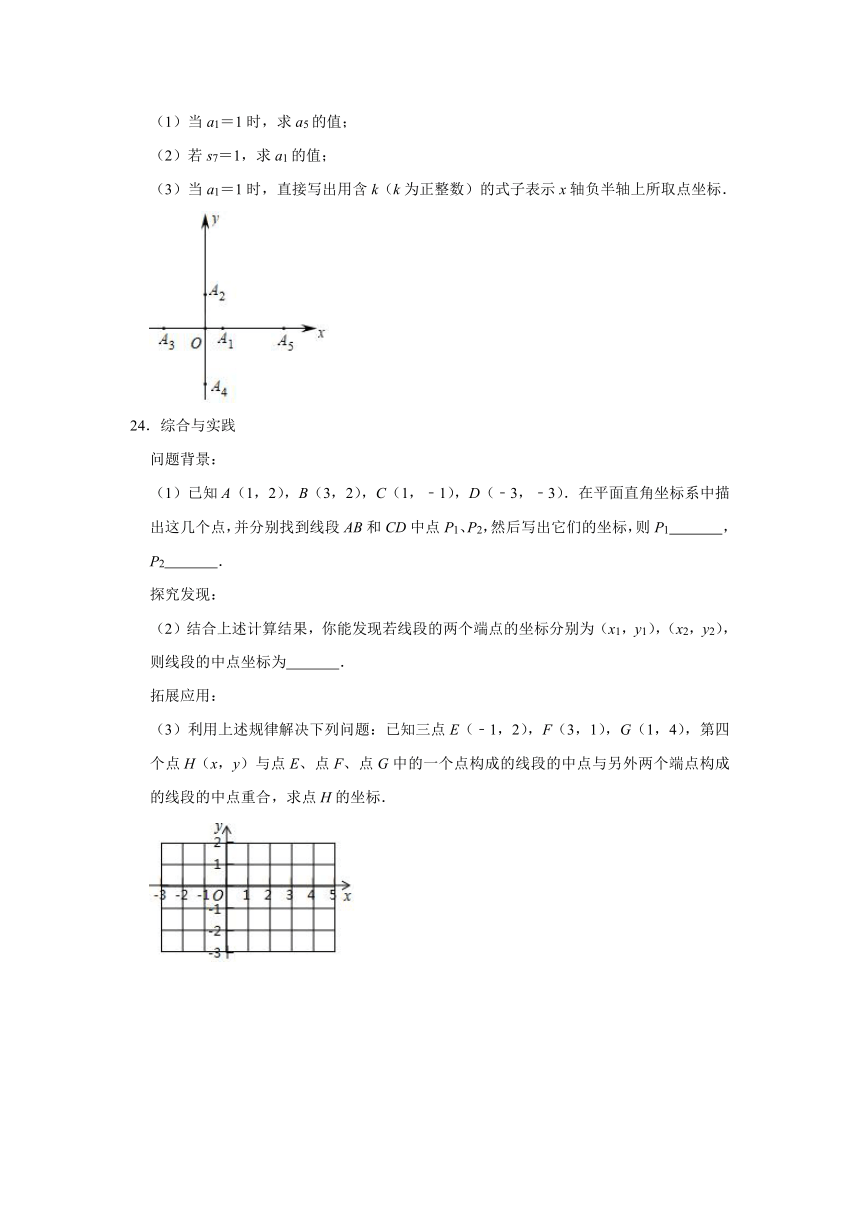
(1)当a1=1时,求a5的值;
(2)若s7=1,求a1的值;
(3)当a1=1时,直接写出用含k(k为正整数)的式子表示x轴负半轴上所取点坐标.
24.综合与实践
问题背景:
(1)已知A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出这几个点,并分别找到线段AB和CD中点P1、P2,然后写出它们的坐标,则P1
,P2
.
探究发现:
(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为
.
拓展应用:
(3)利用上述规律解决下列问题:已知三点E(﹣1,2),F(3,1),G(1,4),第四个点H(x,y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.
参考答案
一.选择题(共12小题)
1.
B.
2.
A.
3.
C.
4.
D.
5.
B.
6.
D.
7.
C.
8.
C.
9.
B.
10.B.
11.
A.
12.
A.
二.填空题(共5小题)
13.﹣5.
14.(0,﹣2).
15.(﹣6,8)或(﹣6,﹣8).
16.(﹣7,0).
17.
2.
三.解答题(共7小题)
18.解:(1)∵点P(8﹣2m,m﹣1)在x轴上,
∴m﹣1=0,
解得:m=1;
(2)∵点P到两坐标轴的距离相等,
∴|8﹣2m|=|m﹣1|,
∴8﹣2m=m﹣1或8﹣2m=1﹣m,
解得:m=3或m=7,
∴P(2,2)或(﹣6,6).
19.解:(1)由题意得:m﹣1=0,
解得:m=1;
(2)由题意得:m﹣1=2m+3,
解得:m=﹣4.
20.解(1)因为点A(﹣2,6)的“
级关联点”是点A1,所以A1为A1(5,1).
(2)∵点M(m﹣1,2m)的“﹣3级关联点”为M′(﹣3(m﹣1)+2m,m﹣1+(﹣3)×2m),M′位于y轴上,
∴﹣3(m﹣1)+2m=0,
解得:m=3
∴m﹣1+(﹣3)×2m=﹣16,
∴M′(0,﹣16).
21.解:(1)A(﹣2,1),B(﹣3,﹣2),C(3,﹣2),D(1,2);
(2)S四边形ABCD=3×3+2××1×3+×2×4=16.
22.解:(1)观察图形,可知:A(1,0)、B(1,2)、C(﹣2,2)、D(﹣2,﹣2)、E(3,﹣2);
(2)∵E(3,﹣2),DE=5,
∴EF=6,
∴F(3,4).
23.解:(1)当a1=1时,a2=1+1=2,
a3=﹣(2+1)=﹣3,
a4=﹣(3+1)=﹣4,
a5=4+1=5;
(2)∵a2=a1+1,a3=﹣(a1+2),a4=﹣(a1+3),a5=a1+4,a6=a1+5,a7=﹣(a1+6),
∴s7=a1+a2+…+a7=a1﹣1,
当s1=1时,则a1﹣1=1,
∴a1=2;
(3)∵当a1=1时,则
a3=﹣3,
a7=﹣7,
a11=﹣11,
…
∴a4k﹣1=﹣(4k﹣1)=﹣4k+1
∴A4k﹣1(﹣4k+1,0).
24.解:(1)如图:A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出它们如下:
线段AB和CD中点P1、P2的坐标分别为(2,2)、(﹣1,﹣2)
故答案为:(2,2)、(﹣1,﹣2).
(2)若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为.
故答案为:.
(3)∵E(﹣1,2),F(3,1),G(1,4),
∴EF、FG、EG的中点分别为:(1,)、(2,)、(0,3)
∴①HG过EF中点(1,)时,=1,=
解得:x=1,y=﹣1,故H(1,﹣1);
②EH过FG中点(2,)时,=2,=
解得:x=5,y=3,故H(5,3);
③FH过EG的中点(0,3)时,=0,=3
解得:x=﹣3,y=5,故H(﹣3,5).
∴点H的坐标为:(1,﹣1),(5,3),(﹣3,5).
平面直角坐标系
一.选择题(共12小题)
1.在平面直角坐标系中,点(﹣2,3)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.下列各点中,在第三象限的点是( )
A.(﹣1,﹣4)
B.(1,﹣4)
C.(﹣1,4)
D.(1,4)
3.平面直角坐标系内,下列的点位于第四象限的是( )
A.(﹣3,1)
B.(﹣3,﹣1)
C.(3,﹣1)
D.(0,﹣1)
4.点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )
A.(5,﹣3)
B.(﹣5,3)
C.(3,﹣5)
D.(﹣3,5)
5.在平面直角坐标系中,点(﹣6,7)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6.下列各点中,第四象限内的点是( )
A.(1,2)
B.(﹣2,﹣3)
C.(﹣2,1)
D.(1,﹣2)
7.点P(﹣3,﹣4)位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
8.已知点P(3a,a+2)在x轴上,则P点的坐标是( )
A.(3,2)
B.(6,0)
C.(﹣6,0)
D.(6,2)
9.已知点P(a,b)在第四象限,且点P到x轴的距离为3,到y轴的距离为6,则点P的坐标是( )
A.(3,﹣6)
B.(6,﹣3)
C.(﹣3,6)
D.(﹣3,3)或(﹣6,6)
10.点M(﹣2019,2019)的位置在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
11.如图,动点P从(0,3)出发,沿所示方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2017次碰到矩形的边时,点P的坐标为( )
A.(3,0)
B.(0,3)
C.(1,4)
D.(8,3)
12.如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3,过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2017的横坐标为( )
A.31008
B.0
C.31009
D.31007
二.填空题(共5小题)
13.在平面直角坐标系中,已知点A(2﹣a,2a+3)在第四象限.若点A在两坐标轴夹角平分线上,则a的值为
.
14.如果P(m+3,2m+4)在y轴上,那么点P的坐标是
.
15.已知平面内有一点A的横坐标为﹣6,且到原点的距离等于10,则A点的坐标为
.
16.若点M(a﹣3,a+4)在x轴上,则点M的坐标是
.
17.点P(2,3)到y轴的距离是
.
三.解答题(共7小题)
18.已知点P(8﹣2m,m﹣1).
(1)若点P在x轴上,求m的值.
(2)若点P到两坐标轴的距离相等,求P点的坐标.
19.在平面直角坐标系中,已知点M(m﹣1,2m+3)
(1)若点M在y轴上,求m的值.
(2)若点M在第一、三象限的角平分线上,求m的值.
20.在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”例如,点P(1,4)的“3级美联点”为Q(3×1+4,1+3×4),即Q(7,13).
(1)已知点A(﹣2,6)的“级关联点”是点A1,求点A1的坐标.
(2)已知点M(m﹣1,2m)的“﹣3级关联点”M′位于y轴上.求点M′的坐标.
21.如图,已知四边形ABCD.
(1)写出点A,B,C,D的坐标;
(2)试求四边形ABCD的面积.(网格中每个小正方形的边长均为1)
22.每个小方格都是边长为1的正方形,在平面直角坐标系中.
(1)写出图中从原点O出发,按箭头所指方向先后经过的A、B、C、D、E这几个点点的坐标;
(2)按图中所示规律,找到下一个点F的位置并写出它的坐标.
23.如图,在直角坐标系的坐标轴上按如下规律取点:A1在x轴正半轴上,A2在y轴正半轴上,A3在x轴负半轴上,A4在y轴负半轴上,A5在x轴正半轴上,…,且OA1+1=OA2,OA2+1=OA3,OA3+1=OA4…,设A1,A2,A3,A4…,有坐标分别为(a1,0),(0,a2),(a3,0),(0,a4)…,sn=a1+a2+a3+…+an.
(1)当a1=1时,求a5的值;
(2)若s7=1,求a1的值;
(3)当a1=1时,直接写出用含k(k为正整数)的式子表示x轴负半轴上所取点坐标.
24.综合与实践
问题背景:
(1)已知A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出这几个点,并分别找到线段AB和CD中点P1、P2,然后写出它们的坐标,则P1
,P2
.
探究发现:
(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为
.
拓展应用:
(3)利用上述规律解决下列问题:已知三点E(﹣1,2),F(3,1),G(1,4),第四个点H(x,y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.
参考答案
一.选择题(共12小题)
1.
B.
2.
A.
3.
C.
4.
D.
5.
B.
6.
D.
7.
C.
8.
C.
9.
B.
10.B.
11.
A.
12.
A.
二.填空题(共5小题)
13.﹣5.
14.(0,﹣2).
15.(﹣6,8)或(﹣6,﹣8).
16.(﹣7,0).
17.
2.
三.解答题(共7小题)
18.解:(1)∵点P(8﹣2m,m﹣1)在x轴上,
∴m﹣1=0,
解得:m=1;
(2)∵点P到两坐标轴的距离相等,
∴|8﹣2m|=|m﹣1|,
∴8﹣2m=m﹣1或8﹣2m=1﹣m,
解得:m=3或m=7,
∴P(2,2)或(﹣6,6).
19.解:(1)由题意得:m﹣1=0,
解得:m=1;
(2)由题意得:m﹣1=2m+3,
解得:m=﹣4.
20.解(1)因为点A(﹣2,6)的“
级关联点”是点A1,所以A1为A1(5,1).
(2)∵点M(m﹣1,2m)的“﹣3级关联点”为M′(﹣3(m﹣1)+2m,m﹣1+(﹣3)×2m),M′位于y轴上,
∴﹣3(m﹣1)+2m=0,
解得:m=3
∴m﹣1+(﹣3)×2m=﹣16,
∴M′(0,﹣16).
21.解:(1)A(﹣2,1),B(﹣3,﹣2),C(3,﹣2),D(1,2);
(2)S四边形ABCD=3×3+2××1×3+×2×4=16.
22.解:(1)观察图形,可知:A(1,0)、B(1,2)、C(﹣2,2)、D(﹣2,﹣2)、E(3,﹣2);
(2)∵E(3,﹣2),DE=5,
∴EF=6,
∴F(3,4).
23.解:(1)当a1=1时,a2=1+1=2,
a3=﹣(2+1)=﹣3,
a4=﹣(3+1)=﹣4,
a5=4+1=5;
(2)∵a2=a1+1,a3=﹣(a1+2),a4=﹣(a1+3),a5=a1+4,a6=a1+5,a7=﹣(a1+6),
∴s7=a1+a2+…+a7=a1﹣1,
当s1=1时,则a1﹣1=1,
∴a1=2;
(3)∵当a1=1时,则
a3=﹣3,
a7=﹣7,
a11=﹣11,
…
∴a4k﹣1=﹣(4k﹣1)=﹣4k+1
∴A4k﹣1(﹣4k+1,0).
24.解:(1)如图:A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出它们如下:
线段AB和CD中点P1、P2的坐标分别为(2,2)、(﹣1,﹣2)
故答案为:(2,2)、(﹣1,﹣2).
(2)若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为.
故答案为:.
(3)∵E(﹣1,2),F(3,1),G(1,4),
∴EF、FG、EG的中点分别为:(1,)、(2,)、(0,3)
∴①HG过EF中点(1,)时,=1,=
解得:x=1,y=﹣1,故H(1,﹣1);
②EH过FG中点(2,)时,=2,=
解得:x=5,y=3,故H(5,3);
③FH过EG的中点(0,3)时,=0,=3
解得:x=﹣3,y=5,故H(﹣3,5).
∴点H的坐标为:(1,﹣1),(5,3),(﹣3,5).
