人教版七年级数学下册 5.4 平移 同步练习 试题含答案
文档属性
| 名称 | 人教版七年级数学下册 5.4 平移 同步练习 试题含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 143.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-08 21:50:32 | ||
图片预览


文档简介
5.4
平移
一.选择题(共8小题)
1.下列现象中是平移的是( )
A.将一张纸沿它的中线折叠
B.电梯的上下移动
C.飞碟的快速转动
D.翻开书中的每一页纸张
2.在下图所示的四个三角形中,能由△ABC经过平移得到的是( )
A.
B.
C.
D.
3.下列现象属于平移的是( )
①打气筒活塞的轮复运动,②电梯的上下运动,③钟摆的摆动,④转动的门,⑤汽车在一条笔直的马路上行走.
A.③
B.②③
C.①②④
D.①②⑤
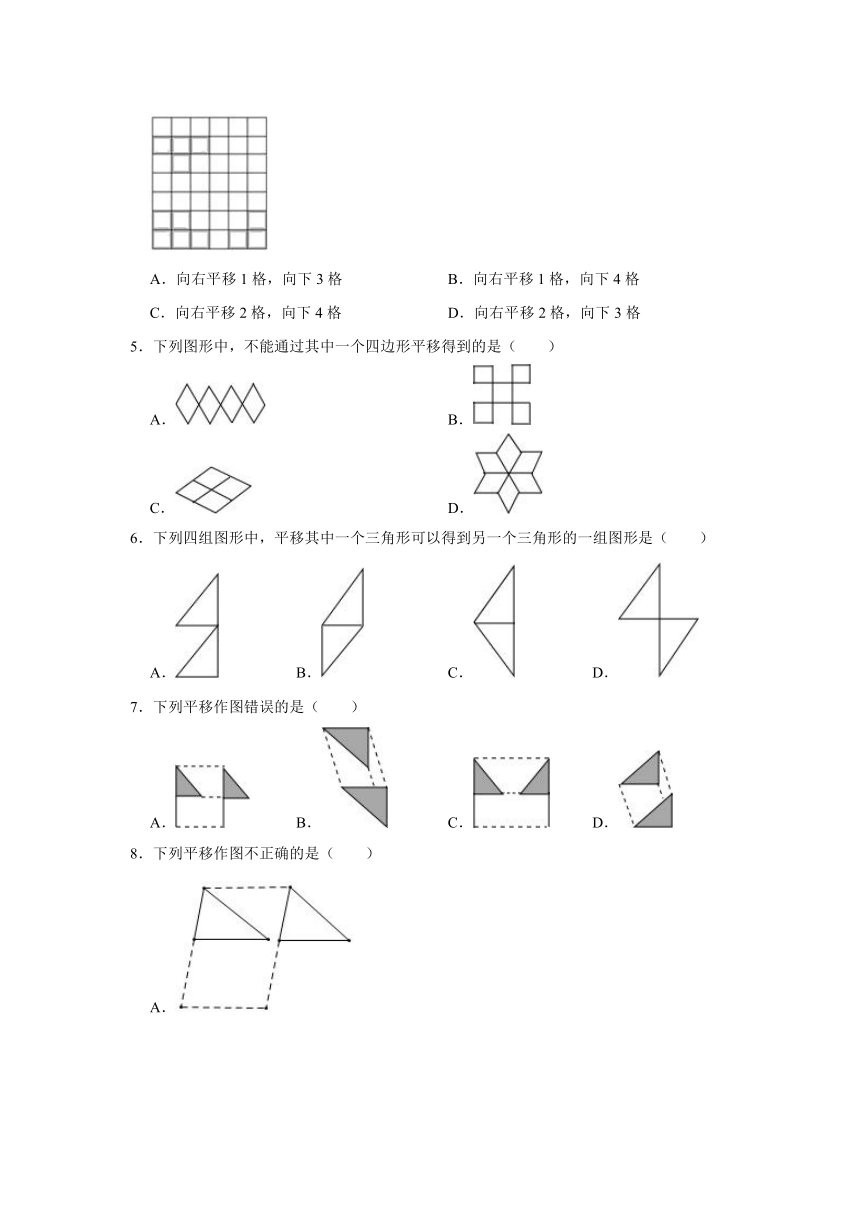
4.如图所示,共有3个方格块,现在要把上面的方格块与下面的两个方格块合成一个长方形的整体,则应将上面的方格块( )
A.向右平移1格,向下3格
B.向右平移1格,向下4格
C.向右平移2格,向下4格
D.向右平移2格,向下3格
5.下列图形中,不能通过其中一个四边形平移得到的是( )
A.
B.
C.
D.
6.下列四组图形中,平移其中一个三角形可以得到另一个三角形的一组图形是( )
A.
B.
C.
D.
7.下列平移作图错误的是( )
A.
B.
C.
D.
8.下列平移作图不正确的是( )
A.
B.
C.
D.
二.填空题(共6小题)
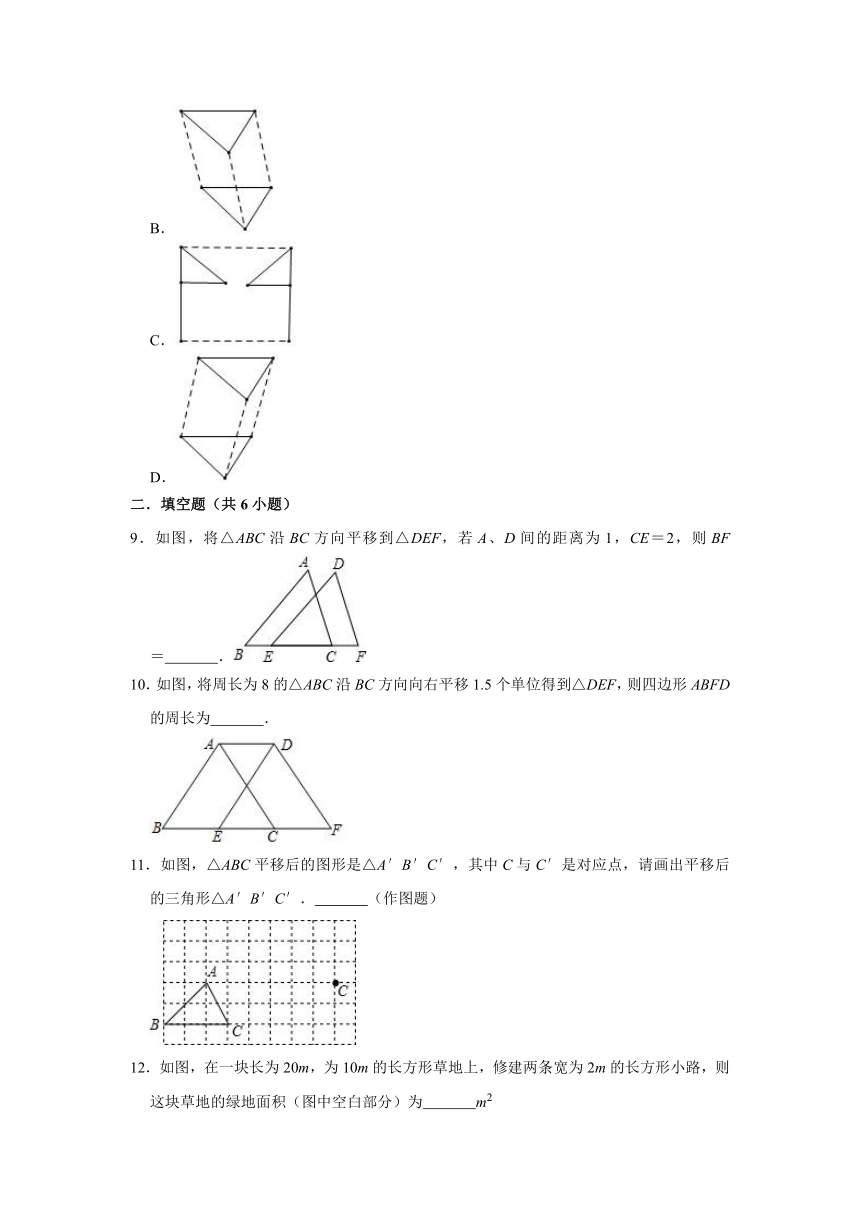
9.如图,将△ABC沿BC方向平移到△DEF,若A、D间的距离为1,CE=2,则BF=
.
10.如图,将周长为8的△ABC沿BC方向向右平移1.5个单位得到△DEF,则四边形ABFD的周长为
.
11.如图,△ABC平移后的图形是△A′B′C′,其中C与C′是对应点,请画出平移后的三角形△A′B′C′.
(作图题)
12.如图,在一块长为20m,为10m的长方形草地上,修建两条宽为2m的长方形小路,则这块草地的绿地面积(图中空白部分)为
m2
13.如图,在△ABC中,∠B=90°,BC=5cm,AB=12cm,则图中4个小直角三角形周长的和为
.
14.如图是一块长方形ABCD的场地,长AB=a米,宽AD=b米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为
米2.
三.解答题(共6小题)
15.如图,将三角形ABC水平向右平移得到三角形DEF,A,D两点的距离为1,CE=2,∠A=70°.根据题意完成下列各题:
(1)AC和DF的数量关系为
;AC和DF的位置关系为
;
(2)∠1=
度
(3)BF=
.
16.如图,已知直线AB∥CD,∠A=∠C=100°,E,F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由;
(2)求∠DBE的度数;
(3)若平行移动AD,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出∠ADB;若不存在,请说明理由.
17.如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE=
cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
18.如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(3,2).
(1)填空:点A的坐标是
,点B
的坐标是
;
(2)将△ABC先向左平移3个单位长度,再向上平移1个单位长度,画出平移后的△A1B1C1;
(3)求△ABC的面积.
19.如图,在正方形网格中有一个△ABC,按要求进行下列作图(只借助网格,需要写出结论).
(1)过点B画出AC的平行线;
(2)画出三角形ABC向右平移5格,在向上平移2格后的△DEF;
(3)若每一个网格的单位长度为a,求三角形ABC的面积.
20.如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?
参考答案
一.选择题(共8小题)
1.
B.
2.
C.
3.
D.
4.
C.
5.
D.
6.
A.
7.
C.
8.
C.
二.填空题(共6小题)
9.
BF=BE+EC+CF=4.
10.
11.
11.作法:(1)连接CC′,过点C作A′C′∥AC,且相等,再过点A′,作A′B′∥AB且相等,连接A′、B′、C′,△A′B′C′就是所画的三角形.
12.
144.
13.
30
14.(ab﹣a﹣2b+2).
三.解答题(共6小题)
15.解:(1)AC和DF的关系式为AC=DF,AC∥DF.
(2)∵三角形ABC水平向右平移得到三角形DEF,
∴AB∥DE,
∵∠A=70°,
∴∠1=110(度);
(3)BF=BE+CE+CF=2+1+1=4.
故答案为:AC=DF,AC∥DF;110;4;
16.解:(1)直线AD与BC互相平行,理由:
∵AB∥CD,
∴∠A+∠ADC=180°,
又∵∠A=∠C
∴∠ADC+∠C=180°,
∴AD∥BC;
(2)∵AB∥CD,
∴∠ABC=180°﹣∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE=∠ABF+∠CBF=∠ABC=40°;
(3)存在.
设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°﹣∠A=80°,
∴∠ADB=80°﹣x°.
若∠BEC=∠ADB,
则x°+40°=80°﹣x°,
得x°=20°.
∴存在∠BEC=∠ADB=60°.
17.解:(1)∵将△ABC沿直线AB向右平移得到△BDE,
∴△ABC≌△BDE,
∴BE=AC=6cm,
故答案为:6;
(2)由(1)知△ABC≌△BDE,
∴∠DBE=∠CAB=50°、∠BDE=∠ABC=100°,
∴∠CBE=180°﹣∠ABC﹣∠DBE=30°.
18.解:(1)点A的坐标是:(4,﹣1),点B
的坐标是:(5,3);
故答案为:(4,﹣1),(5,3);
(2)如图所示:△A1B1C1,即为所求;
(3).
19.解:(1)如图,直线BP为所作.
(2)如图,△DEF为所作;
(3)三角形ABC的面积=×3a×2a=3a2.
20.解:如图,利用平移线段,把楼梯的横竖向上向右平移,构成一个矩形,长宽分别为8米,6米,
即可得地毯的长度为6+8=14(米),地毯的面积为14×2=28(平方米),
故买地毯至少需要28×60=1680(元).
购买地毯需要1680元.
平移
一.选择题(共8小题)
1.下列现象中是平移的是( )
A.将一张纸沿它的中线折叠
B.电梯的上下移动
C.飞碟的快速转动
D.翻开书中的每一页纸张
2.在下图所示的四个三角形中,能由△ABC经过平移得到的是( )
A.
B.
C.
D.
3.下列现象属于平移的是( )
①打气筒活塞的轮复运动,②电梯的上下运动,③钟摆的摆动,④转动的门,⑤汽车在一条笔直的马路上行走.
A.③
B.②③
C.①②④
D.①②⑤
4.如图所示,共有3个方格块,现在要把上面的方格块与下面的两个方格块合成一个长方形的整体,则应将上面的方格块( )
A.向右平移1格,向下3格
B.向右平移1格,向下4格
C.向右平移2格,向下4格
D.向右平移2格,向下3格
5.下列图形中,不能通过其中一个四边形平移得到的是( )
A.
B.
C.
D.
6.下列四组图形中,平移其中一个三角形可以得到另一个三角形的一组图形是( )
A.
B.
C.
D.
7.下列平移作图错误的是( )
A.
B.
C.
D.
8.下列平移作图不正确的是( )
A.
B.
C.
D.
二.填空题(共6小题)
9.如图,将△ABC沿BC方向平移到△DEF,若A、D间的距离为1,CE=2,则BF=
.
10.如图,将周长为8的△ABC沿BC方向向右平移1.5个单位得到△DEF,则四边形ABFD的周长为
.
11.如图,△ABC平移后的图形是△A′B′C′,其中C与C′是对应点,请画出平移后的三角形△A′B′C′.
(作图题)
12.如图,在一块长为20m,为10m的长方形草地上,修建两条宽为2m的长方形小路,则这块草地的绿地面积(图中空白部分)为
m2
13.如图,在△ABC中,∠B=90°,BC=5cm,AB=12cm,则图中4个小直角三角形周长的和为
.
14.如图是一块长方形ABCD的场地,长AB=a米,宽AD=b米,从A、B两处入口的小路宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为
米2.
三.解答题(共6小题)
15.如图,将三角形ABC水平向右平移得到三角形DEF,A,D两点的距离为1,CE=2,∠A=70°.根据题意完成下列各题:
(1)AC和DF的数量关系为
;AC和DF的位置关系为
;
(2)∠1=
度
(3)BF=
.
16.如图,已知直线AB∥CD,∠A=∠C=100°,E,F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由;
(2)求∠DBE的度数;
(3)若平行移动AD,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出∠ADB;若不存在,请说明理由.
17.如图,将△ABC沿直线AB向右平移后到达△BDE的位置.
(1)若AC=6cm,则BE=
cm;
(2)若∠CAB=50°,∠BDE=100°,求∠CBE的度数.
18.如图,平面直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(3,2).
(1)填空:点A的坐标是
,点B
的坐标是
;
(2)将△ABC先向左平移3个单位长度,再向上平移1个单位长度,画出平移后的△A1B1C1;
(3)求△ABC的面积.
19.如图,在正方形网格中有一个△ABC,按要求进行下列作图(只借助网格,需要写出结论).
(1)过点B画出AC的平行线;
(2)画出三角形ABC向右平移5格,在向上平移2格后的△DEF;
(3)若每一个网格的单位长度为a,求三角形ABC的面积.
20.如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?
参考答案
一.选择题(共8小题)
1.
B.
2.
C.
3.
D.
4.
C.
5.
D.
6.
A.
7.
C.
8.
C.
二.填空题(共6小题)
9.
BF=BE+EC+CF=4.
10.
11.
11.作法:(1)连接CC′,过点C作A′C′∥AC,且相等,再过点A′,作A′B′∥AB且相等,连接A′、B′、C′,△A′B′C′就是所画的三角形.
12.
144.
13.
30
14.(ab﹣a﹣2b+2).
三.解答题(共6小题)
15.解:(1)AC和DF的关系式为AC=DF,AC∥DF.
(2)∵三角形ABC水平向右平移得到三角形DEF,
∴AB∥DE,
∵∠A=70°,
∴∠1=110(度);
(3)BF=BE+CE+CF=2+1+1=4.
故答案为:AC=DF,AC∥DF;110;4;
16.解:(1)直线AD与BC互相平行,理由:
∵AB∥CD,
∴∠A+∠ADC=180°,
又∵∠A=∠C
∴∠ADC+∠C=180°,
∴AD∥BC;
(2)∵AB∥CD,
∴∠ABC=180°﹣∠C=80°,
∵∠DBF=∠ABD,BE平分∠CBF,
∴∠DBE=∠ABF+∠CBF=∠ABC=40°;
(3)存在.
设∠ABD=∠DBF=∠BDC=x°.
∵AB∥CD,
∴∠BEC=∠ABE=x°+40°;
∵AB∥CD,
∴∠ADC=180°﹣∠A=80°,
∴∠ADB=80°﹣x°.
若∠BEC=∠ADB,
则x°+40°=80°﹣x°,
得x°=20°.
∴存在∠BEC=∠ADB=60°.
17.解:(1)∵将△ABC沿直线AB向右平移得到△BDE,
∴△ABC≌△BDE,
∴BE=AC=6cm,
故答案为:6;
(2)由(1)知△ABC≌△BDE,
∴∠DBE=∠CAB=50°、∠BDE=∠ABC=100°,
∴∠CBE=180°﹣∠ABC﹣∠DBE=30°.
18.解:(1)点A的坐标是:(4,﹣1),点B
的坐标是:(5,3);
故答案为:(4,﹣1),(5,3);
(2)如图所示:△A1B1C1,即为所求;
(3).
19.解:(1)如图,直线BP为所作.
(2)如图,△DEF为所作;
(3)三角形ABC的面积=×3a×2a=3a2.
20.解:如图,利用平移线段,把楼梯的横竖向上向右平移,构成一个矩形,长宽分别为8米,6米,
即可得地毯的长度为6+8=14(米),地毯的面积为14×2=28(平方米),
故买地毯至少需要28×60=1680(元).
购买地毯需要1680元.
