北师大版八年级下册数学第四章因式分解复习课件(WPS打开,共25张PPT)
文档属性
| 名称 | 北师大版八年级下册数学第四章因式分解复习课件(WPS打开,共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 376.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第
四
章
因式分解
复习课件
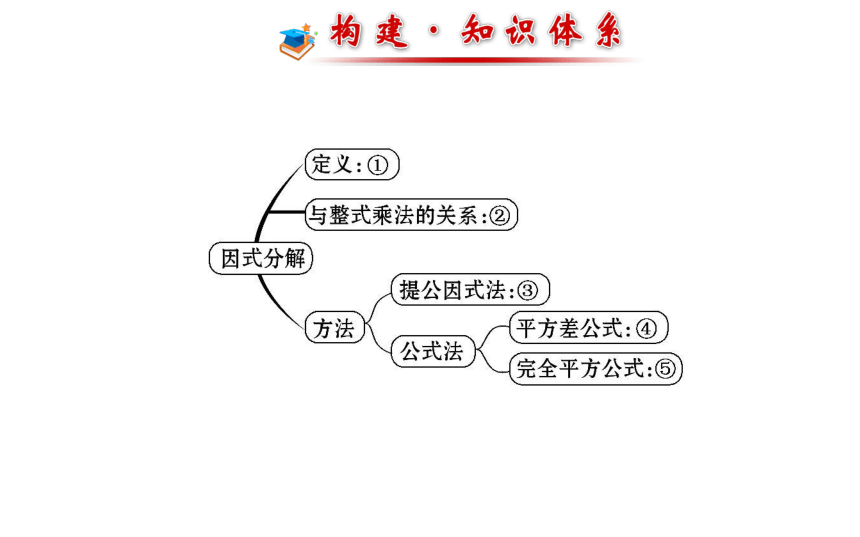
请写出框图中数字处的内容:
①____________________________________________________
_______________;
②_____;
③____________________________________________________
_____________;
④________________;
⑤__________________.
把一个多项式表示成若干个多项式乘积的形式,称为把这个
多项式因式分解
互逆
把多项式各项都有的公因式提到括号外面,进而把多项式因
式分解的方法
a2-b2=(a+b)(a-b)
a2±2ab+b2=(a±b)2
考点
1
用提公因式法因式分解?
【知识点睛】
用提公因式法进行因式分解时,最关键的一步是确定公因式.寻找公因式时,对于数字因数找各项数字的最大公约数,对于相同的字母,找相同字母的最低次幂.
【例1】因式分解:m2-5m= .
【思路点拨】找公因式→提公因式→结果.
【自主解答】提取公因式m,
得m2-5m=
m(m-5).
答案:m(m-5)
【中考集训】
1.因式分解:x2+xy= .
【解析】x2+xy=x·x+x·y
=x(x+y).
答案:x(x+y)
2.因式分解:m2-2m= .
【解析】m2-2m=m(m-2).
答案:m(m-2)
3.多项式ax2-a与多项式x2-2x+1的公因式是 .
【解析】ax2-a=a(x+1)(x-1);
x2-2x+1=(x-1)2,
则公因式为x-1.
答案:x-1
4.因式分解:2xy-4x2= .
【解析】原式=2x(y-2x).
答案:2x(y-2x)
考点
2
用公式法因式分解?
【知识点睛】
符合用平方差公式因式分解的多项式一般有以下特点:
1.有两项.
2.两项都能写成平方的形式.
3.符号相反.
符合用完全平方公式因式分解的多项式一般有以下特点:
1.有三项.
2.其中有两项同号,且此两项能写成两数或两式的平方的形式.
3.另一项是这两数(或两式)的乘积(或乘积相反数)的2倍.
【例2】因式分解4x-x3= .
【思路点拨】找公因式→提公因式→继续分解→平方差公式→结果.
【自主解答】4x-x3=x(4-x2)
=x(2+x)(2-x).
答案:x(2+x)(2-x)
【中考集训】
1.因式分解:2a2-8= .
【解析】2a2-8=2(a2-4)
=2(a+2)(a-2).
答案:2(a+2)(a-2)
2.因式分解:4-a2= .
【解析】4-a2=(2+a)(2-a).
答案:(2+a)(2-a)
3.因式分解:x2y-y= .
【解析】原式=y(x2-1)
=y(x+1)(x-1).
答案:y(x+1)(x-1)
4.把多项式因式分解:ax2-ay2= .
【解析】先提取公因式a,再根据平方差公式进行二次分解.注意平方差公式:a2-b2=(a+b)(a-b),
则ax2-ay2=a(x2-y2)=a(x+y)(x-y).
答案:a(x+y)(x-y)
5.因式分解:ab2-4a= .
【解析】ab2-4a=a(b2-4)
=a(b-2)(b+2).
答案:a(b-2)(b+2)
考点
3
因式分解的简单应用?
【知识点睛】
因式分解是代数运算中的一种重要的恒等变形,其应用非常广泛,特别是对于含有条件限制的多项式求值,如果考虑利用因式分解将所求多项式进行适当变形,转化为已知条件,往往能收到事半功倍的效果.
【例3】在日常生活中,如取款、上网等都需要密码,有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4-y4,因式分解的结果是(x-y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3-xy2,取x=10,y=10时,用上述方法产生的密码有哪些?
【思路点拨】先将给定的多项式因式分解,然后计算出各部分对应值,进而得出有关的密码.
【自主解答】因为4x3-xy2=x(4x2-y2)
=x(2x+y)(2x-y),
所以当x=10,y=10时,
有x=10,(2x+y)=20+10=30,
(2x-y)=20-10=10,
所以产生的密码是101030或103010或301010.
【中考集训】
1.已知a,b满足a+b=5,且a2b+ab2=-10,则ab的值是( )
A.-2
B.2
C.-50
D.50
【解析】选A.a2b+ab2=ab(a+b)=-10,
所以5ab=-10,故ab=-2.
2.若m-n=-1,则(m-n)2-2m+2n的值是( )
A.3
B.2
C.1
D.-1
【解析】选A.(m-n)2-2m+2n
=(m-n)2-2(m-n)
=(m-n)(m-n-2).
因为m-n=-1,
所以原式=(-1)×(-1-2)=3.
3.若a2+2a=1,则2a2+4a+1= .
【解析】2a2+4a+1
=(2a2+4a)+1
=2(a2+2a)+1
=2×1+1
=3.
答案:3
4.已知a+b=4,a-b=3,则a2-b2= .
【解析】a2-b2=(a+b)(a-b)=4×3=12.
答案:12
5.若m2-n2=6,且m-n=2,则m+n= .
【解析】由m2-n2=6得(m+n)(m-n)=6,
当m-n=2时,2(m+n)=6,解得m+n=3.
答案:3
第
四
章
因式分解
复习课件
请写出框图中数字处的内容:
①____________________________________________________
_______________;
②_____;
③____________________________________________________
_____________;
④________________;
⑤__________________.
把一个多项式表示成若干个多项式乘积的形式,称为把这个
多项式因式分解
互逆
把多项式各项都有的公因式提到括号外面,进而把多项式因
式分解的方法
a2-b2=(a+b)(a-b)
a2±2ab+b2=(a±b)2
考点
1
用提公因式法因式分解?
【知识点睛】
用提公因式法进行因式分解时,最关键的一步是确定公因式.寻找公因式时,对于数字因数找各项数字的最大公约数,对于相同的字母,找相同字母的最低次幂.
【例1】因式分解:m2-5m= .
【思路点拨】找公因式→提公因式→结果.
【自主解答】提取公因式m,
得m2-5m=
m(m-5).
答案:m(m-5)
【中考集训】
1.因式分解:x2+xy= .
【解析】x2+xy=x·x+x·y
=x(x+y).
答案:x(x+y)
2.因式分解:m2-2m= .
【解析】m2-2m=m(m-2).
答案:m(m-2)
3.多项式ax2-a与多项式x2-2x+1的公因式是 .
【解析】ax2-a=a(x+1)(x-1);
x2-2x+1=(x-1)2,
则公因式为x-1.
答案:x-1
4.因式分解:2xy-4x2= .
【解析】原式=2x(y-2x).
答案:2x(y-2x)
考点
2
用公式法因式分解?
【知识点睛】
符合用平方差公式因式分解的多项式一般有以下特点:
1.有两项.
2.两项都能写成平方的形式.
3.符号相反.
符合用完全平方公式因式分解的多项式一般有以下特点:
1.有三项.
2.其中有两项同号,且此两项能写成两数或两式的平方的形式.
3.另一项是这两数(或两式)的乘积(或乘积相反数)的2倍.
【例2】因式分解4x-x3= .
【思路点拨】找公因式→提公因式→继续分解→平方差公式→结果.
【自主解答】4x-x3=x(4-x2)
=x(2+x)(2-x).
答案:x(2+x)(2-x)
【中考集训】
1.因式分解:2a2-8= .
【解析】2a2-8=2(a2-4)
=2(a+2)(a-2).
答案:2(a+2)(a-2)
2.因式分解:4-a2= .
【解析】4-a2=(2+a)(2-a).
答案:(2+a)(2-a)
3.因式分解:x2y-y= .
【解析】原式=y(x2-1)
=y(x+1)(x-1).
答案:y(x+1)(x-1)
4.把多项式因式分解:ax2-ay2= .
【解析】先提取公因式a,再根据平方差公式进行二次分解.注意平方差公式:a2-b2=(a+b)(a-b),
则ax2-ay2=a(x2-y2)=a(x+y)(x-y).
答案:a(x+y)(x-y)
5.因式分解:ab2-4a= .
【解析】ab2-4a=a(b2-4)
=a(b-2)(b+2).
答案:a(b-2)(b+2)
考点
3
因式分解的简单应用?
【知识点睛】
因式分解是代数运算中的一种重要的恒等变形,其应用非常广泛,特别是对于含有条件限制的多项式求值,如果考虑利用因式分解将所求多项式进行适当变形,转化为已知条件,往往能收到事半功倍的效果.
【例3】在日常生活中,如取款、上网等都需要密码,有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4-y4,因式分解的结果是(x-y)(x+y)(x2+y2),若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,(x2+y2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3-xy2,取x=10,y=10时,用上述方法产生的密码有哪些?
【思路点拨】先将给定的多项式因式分解,然后计算出各部分对应值,进而得出有关的密码.
【自主解答】因为4x3-xy2=x(4x2-y2)
=x(2x+y)(2x-y),
所以当x=10,y=10时,
有x=10,(2x+y)=20+10=30,
(2x-y)=20-10=10,
所以产生的密码是101030或103010或301010.
【中考集训】
1.已知a,b满足a+b=5,且a2b+ab2=-10,则ab的值是( )
A.-2
B.2
C.-50
D.50
【解析】选A.a2b+ab2=ab(a+b)=-10,
所以5ab=-10,故ab=-2.
2.若m-n=-1,则(m-n)2-2m+2n的值是( )
A.3
B.2
C.1
D.-1
【解析】选A.(m-n)2-2m+2n
=(m-n)2-2(m-n)
=(m-n)(m-n-2).
因为m-n=-1,
所以原式=(-1)×(-1-2)=3.
3.若a2+2a=1,则2a2+4a+1= .
【解析】2a2+4a+1
=(2a2+4a)+1
=2(a2+2a)+1
=2×1+1
=3.
答案:3
4.已知a+b=4,a-b=3,则a2-b2= .
【解析】a2-b2=(a+b)(a-b)=4×3=12.
答案:12
5.若m2-n2=6,且m-n=2,则m+n= .
【解析】由m2-n2=6得(m+n)(m-n)=6,
当m-n=2时,2(m+n)=6,解得m+n=3.
答案:3
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
