2.4.1平面向量数量积的物理背景及几何意义-人教A版高中数学必修四课件(共15张PPT)
文档属性
| 名称 | 2.4.1平面向量数量积的物理背景及几何意义-人教A版高中数学必修四课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 497.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
2.4.1
平面向量数量积物理背景
及其含义
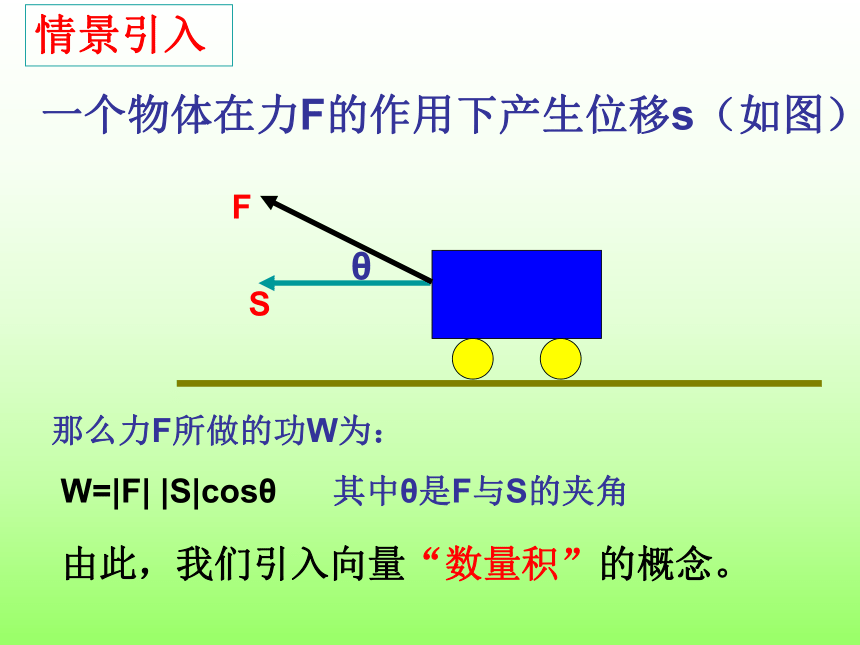
一个物体在力F的作用下产生位移s(如图)
θ
F
S
那么力F所做的功W为:
情景引入
W=|F|
|S|cosθ
其中θ是F与S的夹角
由此,我们引入向量“数量积”的概念。
数量积的定义
(1)两向量的数量积是一个数量,
注意
(2)零向量与任一向量的数量积是等于0.
a·b=|a|
|b|
cosθ
当0°≤θ
<
90°时,a·b为
正;
当90°<θ
≤180°时,a·b为
负。
当
θ
=90°时,
a·b为
零。
cos0°
cos30°
cos45°
cos60°
cos90°
cos120°
cos135°
cos150°
1
0
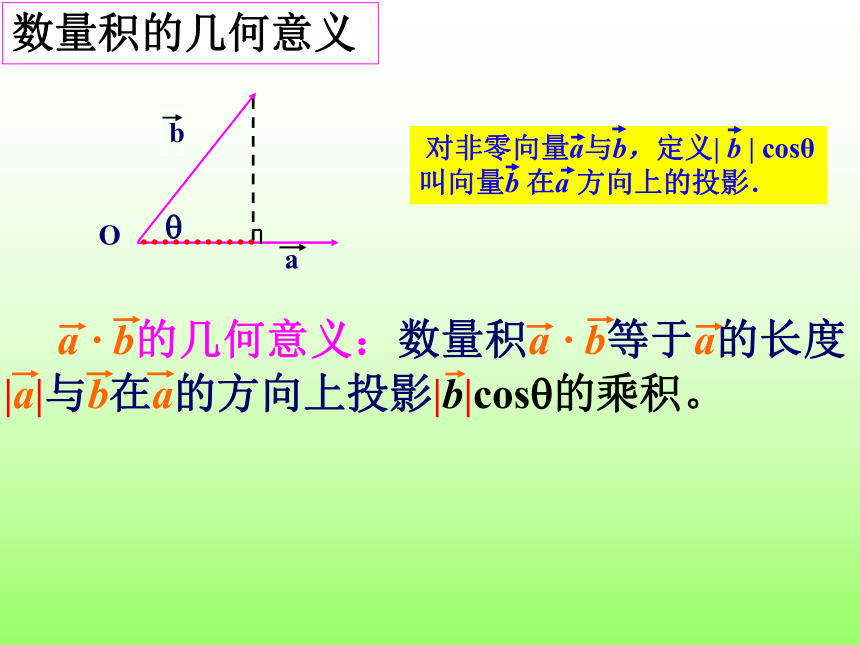
数量积的几何意义
例题讲解
120?
特别地
(求模的方法)
(判断垂直的
又一条件)
(求角度)
回顾实数运算中有关的运算律,类比数量积得运算律:
在实数中
在向量运算中
交换律:
ab=ba
结合律:
(ab)c=a(bc)
分配律:
(a+b)c=ab+bc
消去律:
ab=bc(b≠0)
a=c
数量积的运算律
向量数量积运算不能使用消去律
向量a、b、a
+
b在c上的射影的数量分别是OM、MN、
ON,
证明运算律(3)
典型例题
解:(1)(a+b)2=(a+b)·(a+b)
=(a+b)·a+(a+b)·b
=a·a+b·a+a·b+b·b
=a2+2a·b+b2.
(2)(a+b)·(a-b)=(a+b)·a-(a+b)·b
=a·a+b·a-a·b-b·b
向量的数量积运算类似于多项式运算
夹角的范围
运算律
性
质
数量积公式
知识回顾:
(2)
(交换律)
(分配律)
判断正误:
已知向量
和实数
1.若
,则
中至少有一个为
.
×
×
×
×
√
巩固练习
例4、
已知点O、N、P在△ABC所在平面内,且
A.重心、外心、垂心
B.重心、外心、内心
C.外心、重心、垂心
D.外心、重心、内心
2.4.1
平面向量数量积物理背景
及其含义
一个物体在力F的作用下产生位移s(如图)
θ
F
S
那么力F所做的功W为:
情景引入
W=|F|
|S|cosθ
其中θ是F与S的夹角
由此,我们引入向量“数量积”的概念。
数量积的定义
(1)两向量的数量积是一个数量,
注意
(2)零向量与任一向量的数量积是等于0.
a·b=|a|
|b|
cosθ
当0°≤θ
<
90°时,a·b为
正;
当90°<θ
≤180°时,a·b为
负。
当
θ
=90°时,
a·b为
零。
cos0°
cos30°
cos45°
cos60°
cos90°
cos120°
cos135°
cos150°
1
0
数量积的几何意义
例题讲解
120?
特别地
(求模的方法)
(判断垂直的
又一条件)
(求角度)
回顾实数运算中有关的运算律,类比数量积得运算律:
在实数中
在向量运算中
交换律:
ab=ba
结合律:
(ab)c=a(bc)
分配律:
(a+b)c=ab+bc
消去律:
ab=bc(b≠0)
a=c
数量积的运算律
向量数量积运算不能使用消去律
向量a、b、a
+
b在c上的射影的数量分别是OM、MN、
ON,
证明运算律(3)
典型例题
解:(1)(a+b)2=(a+b)·(a+b)
=(a+b)·a+(a+b)·b
=a·a+b·a+a·b+b·b
=a2+2a·b+b2.
(2)(a+b)·(a-b)=(a+b)·a-(a+b)·b
=a·a+b·a-a·b-b·b
向量的数量积运算类似于多项式运算
夹角的范围
运算律
性
质
数量积公式
知识回顾:
(2)
(交换律)
(分配律)
判断正误:
已知向量
和实数
1.若
,则
中至少有一个为
.
×
×
×
×
√
巩固练习
例4、
已知点O、N、P在△ABC所在平面内,且
A.重心、外心、垂心
B.重心、外心、内心
C.外心、重心、垂心
D.外心、重心、内心
