7.3.2正弦型函数的性质与图像(一)-人教B版(2019)高中数学必修第三册导学案
文档属性
| 名称 | 7.3.2正弦型函数的性质与图像(一)-人教B版(2019)高中数学必修第三册导学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 79.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 00:00:00 | ||
图片预览


文档简介
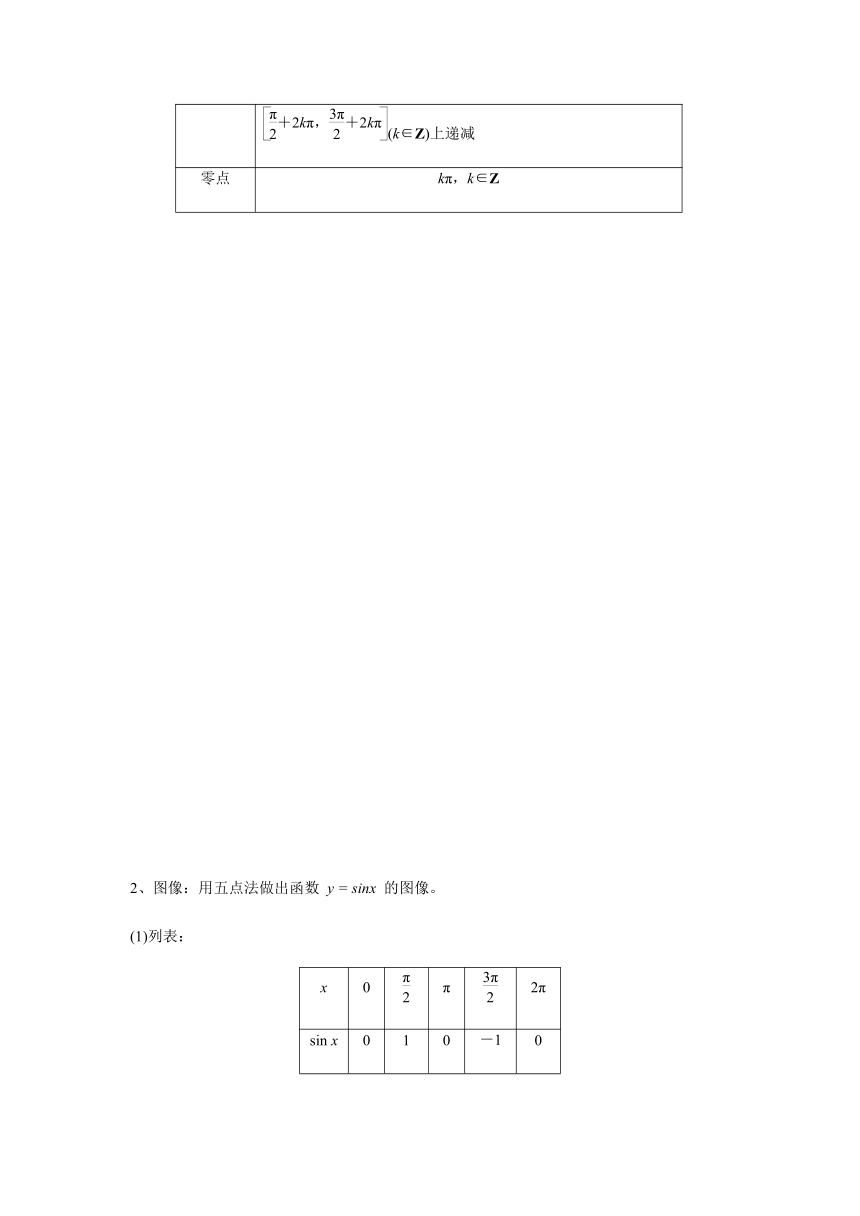
7.3.2 正弦型函数的性质与图像(一)
【学习目标】1.了解正弦型函数
y=Asin(x+)的定义域、值域、周期;
2.了解y=Asin(x+)中的参数A,对函数图像变化的影响;
3.能正确使用五点法和图像变换法做出
y=Asin(x+)图像。
【学习重、难点】
学习重点:函数
y=Asin(x+)的性质及图像的应用。
学习难点:用整体思想探究函数
y=Asin(x+)的性质及参数A,对函数图像的影响
一、【复习回顾】正弦函数
y
=
sinx
的性质和图象
性质
名称
性质
y=sin
x
定义域
R
值域
[-1,1]
最值
当且仅当x=+2kπ,k∈Z时,y=sin
x的最大值ymax=1;
当且仅当x=+2kπ,k∈Z时,y=sin
x的最小值ymin=-1
奇偶性
奇函数
周期性
最小正周期:2π
单调性
(k∈Z)上递增;
(k∈Z)上递减
零点
kπ,k∈Z
图像:用五点法做出函数
y
=
sinx
的图像。
(1)列表:
x
0
π
2π
sin
x
0
1
0
-1
0
(2)描点:画正弦函数y=sin
x,x∈[0,2π]的图像,五个关键点是(0,0),,(π,0),,(2π,0).
(3)用光滑曲线顺次连接这五个点,得到正弦曲线的简图.
二、【新知探究】
正弦型函数的定义:形如
(其中A,,都是常数)的函数称为正弦型函数。
探究一:A的作用:研究
y=Asinx
与
y=sinx
的关系
可以看出,函数y=2sinx的定义域为
R
,
因为-1≤sinx≤1,所以
,又因为
时,y=2sinx=
2
;因为
时,y=2sinx=
,所以y=2sinx的值域为
。
函数y=2sinx是周期函数,周期是
。
同理可得定义域为
R
,值域为
,周期是
。
用五点法做出前两个函数在一个周期内的图像。
答案
列表:
x
0
π
2π
y=sinx
0
1
0
-1
0
y
=2
sinx
0
2
0
-2
0
0
0
0
描点、连线
小结1
一般的,函数y
=
Asinx(A≠0)的定义域为
R
,值域为
,周期为
。
2、A的作用:引起值域的改变,这种变换叫
振幅变换
(也叫
纵向伸缩
)。|A|的大小反映了
曲线波动幅度
大小。
图像变换:y
=
sinx
y
=
Asinx
(A>0)
跟踪练习1
说明两个函数图像间的变换。函数y
=
sinx
y
=
4sinx
答案
y
=
sinx
y
=
4sinx
求函数y=8sinx的最大值、最小值和最小正周期。
答案
最大值8,最小值-8,最小正周期
探究二:
x
0
2π
0
1
0
-1
0
小结2
答案
R,,
答案
2.相位变换,平移变换;
;
3.位置不同
跟踪练习二
说明两个函数图像间的变换.
函数y
=
sinx
答案
y
=
sinx
2、将函数y=sinx图象向左平移1个单位,再向右平移3个单位,可以得到函数(
)的图象。
A.y=sin(x+2)
B.y=sin(x-2)
C.y=sin(x+4)
D.y=sin(x-4)
答案B
【课堂小结】
的作用
的作用:使正弦喊叔叔相应的函数值发生变化;
的作用:使正弦函数的图象位置发生平移;
五点法,图象变换法作正弦型函数图象;
数学方法:换元法,数形结合法.
【学习目标】1.了解正弦型函数
y=Asin(x+)的定义域、值域、周期;
2.了解y=Asin(x+)中的参数A,对函数图像变化的影响;
3.能正确使用五点法和图像变换法做出
y=Asin(x+)图像。
【学习重、难点】
学习重点:函数
y=Asin(x+)的性质及图像的应用。
学习难点:用整体思想探究函数
y=Asin(x+)的性质及参数A,对函数图像的影响
一、【复习回顾】正弦函数
y
=
sinx
的性质和图象
性质
名称
性质
y=sin
x
定义域
R
值域
[-1,1]
最值
当且仅当x=+2kπ,k∈Z时,y=sin
x的最大值ymax=1;
当且仅当x=+2kπ,k∈Z时,y=sin
x的最小值ymin=-1
奇偶性
奇函数
周期性
最小正周期:2π
单调性
(k∈Z)上递增;
(k∈Z)上递减
零点
kπ,k∈Z
图像:用五点法做出函数
y
=
sinx
的图像。
(1)列表:
x
0
π
2π
sin
x
0
1
0
-1
0
(2)描点:画正弦函数y=sin
x,x∈[0,2π]的图像,五个关键点是(0,0),,(π,0),,(2π,0).
(3)用光滑曲线顺次连接这五个点,得到正弦曲线的简图.
二、【新知探究】
正弦型函数的定义:形如
(其中A,,都是常数)的函数称为正弦型函数。
探究一:A的作用:研究
y=Asinx
与
y=sinx
的关系
可以看出,函数y=2sinx的定义域为
R
,
因为-1≤sinx≤1,所以
,又因为
时,y=2sinx=
2
;因为
时,y=2sinx=
,所以y=2sinx的值域为
。
函数y=2sinx是周期函数,周期是
。
同理可得定义域为
R
,值域为
,周期是
。
用五点法做出前两个函数在一个周期内的图像。
答案
列表:
x
0
π
2π
y=sinx
0
1
0
-1
0
y
=2
sinx
0
2
0
-2
0
0
0
0
描点、连线
小结1
一般的,函数y
=
Asinx(A≠0)的定义域为
R
,值域为
,周期为
。
2、A的作用:引起值域的改变,这种变换叫
振幅变换
(也叫
纵向伸缩
)。|A|的大小反映了
曲线波动幅度
大小。
图像变换:y
=
sinx
y
=
Asinx
(A>0)
跟踪练习1
说明两个函数图像间的变换。函数y
=
sinx
y
=
4sinx
答案
y
=
sinx
y
=
4sinx
求函数y=8sinx的最大值、最小值和最小正周期。
答案
最大值8,最小值-8,最小正周期
探究二:
x
0
2π
0
1
0
-1
0
小结2
答案
R,,
答案
2.相位变换,平移变换;
;
3.位置不同
跟踪练习二
说明两个函数图像间的变换.
函数y
=
sinx
答案
y
=
sinx
2、将函数y=sinx图象向左平移1个单位,再向右平移3个单位,可以得到函数(
)的图象。
A.y=sin(x+2)
B.y=sin(x-2)
C.y=sin(x+4)
D.y=sin(x-4)
答案B
【课堂小结】
的作用
的作用:使正弦喊叔叔相应的函数值发生变化;
的作用:使正弦函数的图象位置发生平移;
五点法,图象变换法作正弦型函数图象;
数学方法:换元法,数形结合法.
