人教版八年级数学上册11.1.3 三角形的稳定性课件(18张PPT)
文档属性
| 名称 | 人教版八年级数学上册11.1.3 三角形的稳定性课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 697.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
11.1.3
三角形的稳定性
与三角形有关的线段
知识回顾
知识回顾
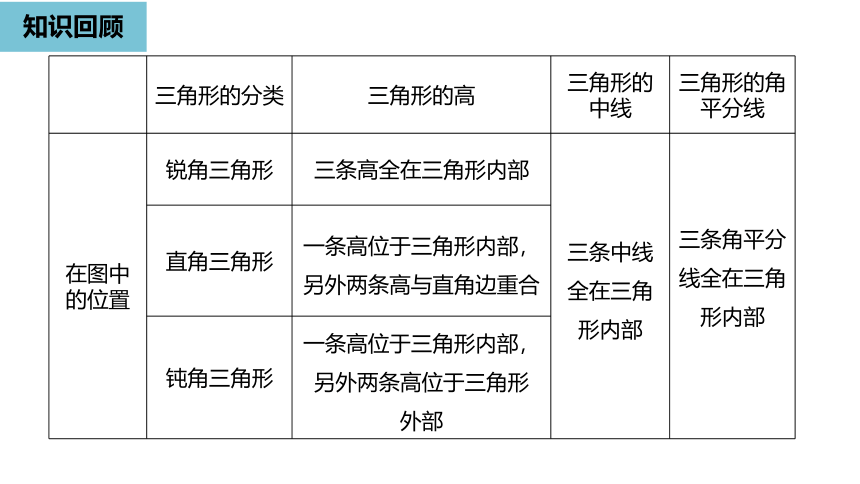
三角形的分类
三角形的高
三角形的中线
三角形的角平分线
在图中的位置
锐角三角形
三条高全在三角形内部
三条中线全在三角形内部
三条角平分线全在三角形内部
直角三角形
一条高位于三角形内部,另外两条高与直角边重合
钝角三角形
一条高位于三角形内部,另外两条高位于三角形
外部
知识回顾
知识回顾
三角形的分类
三角形的高
三角形的中线
三角形的角平分线
交点的
位置
锐角三角形
三条高的交点在三角形内部
三条中线的交点在三角形内部
(重心)
三条角平分线的交点在三角形内部
(内心)
直角三角形
三条高的交点在三角形
直角顶点
钝角三角形
三条高的交点在三角形外部
学习目标
1.了解三角形的稳定性.
2.了解三角形的稳定性和四边形的不稳定性的应用.
3.准确地在生活中使用三角形的稳定性.
课堂导入
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,如图,大家想一想为什么要这样做呢?
工程建筑中经常采用三角形的结构,如屋顶钢架、房梁,其中的道理是什么呢?
生活小常识
新知探究
动手试一试
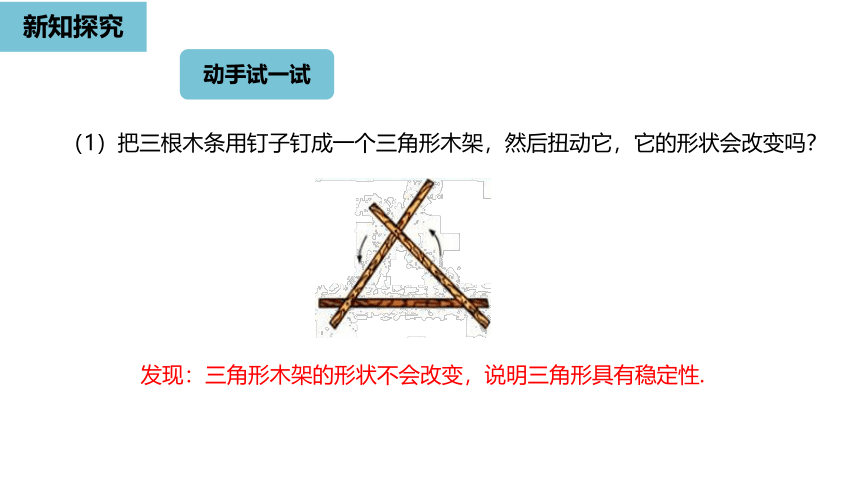
(1)把三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
发现:三角形木架的形状不会改变,说明三角形具有稳定性.
新知探究
动手试一试
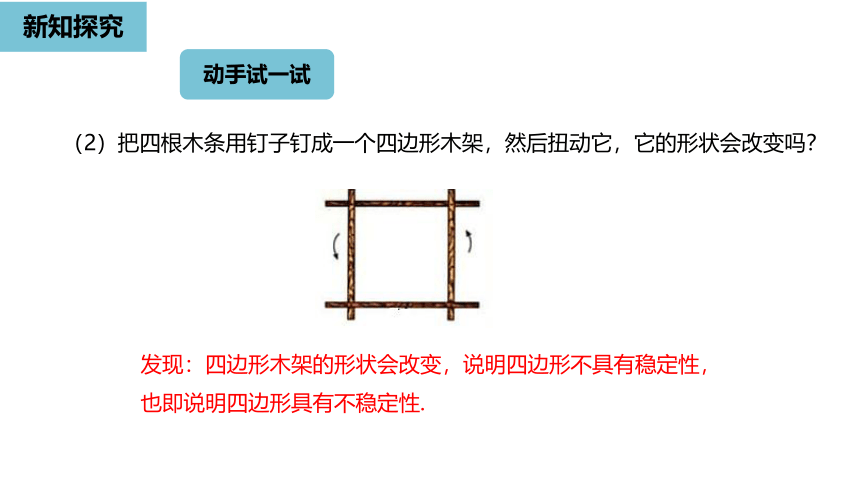
(2)把四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
发现:四边形木架的形状会改变,说明四边形不具有稳定性,
也即说明四边形具有不稳定性.
新知探究
动手试一试
(3)在(2)的四边形木架上再钉一根木条,将四边形的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?为什么?
发现:钉了一根木条的四边形木架的形状不会改变.
原因:斜钉了一根木条后,四边形变成了两个三角形,由于三角形具有稳定性,所以四边形木架的形状不会改变.
知识点1
新知探究
三角形的稳定性
结论:三角形具有稳定性,四边形具有不稳定性,将不稳定的多边形转化为三角形可以使其具有稳定性.
请尝试列举出生活中应用三角形稳定性的例子?
知识点1
新知探究
请尝试列举出生活中应用四边形不稳定性的例子?
三角形的稳定性
跟踪训练
新知探究
1、下列图形哪些具有稳定性?
有
无
无
有
无
有
跟踪训练
新知探究
2、下列关于三角形的稳定性和四边形的不稳定性,说法正确的是(
)
A.稳定性总是有益的,而不稳定性总是有害的
B.稳定性有利用价值,而不稳定性没有利用价值
C.稳定性和不稳定性均有价值
D.以上说法都不对
C
随堂练习
1、下列具有稳定性的是(
)
A.正方形
B.长方形
C.三角形
D.平行四边形
2、木工师傅做完门框后,常常像右图所示一样钉上两条斜拉的木条,
这样做是因为(
).
3、桥梁的斜拉钢索是三角形的结构,主要是为了(
)
A.节约材料,节约成本
B.保持对称性
C.利用三角形的稳定性
D.美观漂亮
C
三角形具有稳定性
C
随堂练习
4、下列设备中没有利用三角形的稳定性的是(
)
A.索道支架
B.起重机
C.屋顶三角形支架
D.活动的四边形衣架
5、电动伸缩门利用了(
)的性质.
6、下图中不具有稳定性的是(
)
D
四边形的不稳定性
A
B
C
D
B
课堂小结
三角形
四边形
稳定性
不稳定性
稳定性和不稳定性在实际生活中发挥不同的作用
将四边形转化成数个三角形,原来的四边形就具有稳定性了.
拓展提升
1
1、(1)要使四边形木架(用四根木条钉成)具有稳定性,至少要再钉上几根木条?
(2)要使五边形木架(用五根木条钉成)具有稳定性,至少要再钉上几根木条?
(3)要使六边形木架(用六根木条钉成)具有稳定性,至少要再钉上几根木条?
拓展提升
1
1、(1)要使四边形木架(用四根木条钉成)具有稳定性,至少要再钉上几根木条?
(2)要使五边形木架(用五根木条钉成)具有稳定性,至少要再钉上几根木条?
(3)要使六边形木架(用六根木条钉成)具有稳定性,至少要再钉上几根木条?
至少再需要1根木条,使得变成2个三角形.
至少再需要2根木条,使得变成3个三角形.
至少再需要3根木条,使得变成4个三角形.
拓展提升
1
1、(4)要使n边形木架(用n根木条钉成)具有稳定性,至少要再钉上几根木条?
根据四边形木架、五边形木架和六边形木架的规律,n边形木架至少再需要(n-3)根木条,使得变成(n-2)个三角形.
学会用数学归纳法解决第(4)问.
11.1.3
三角形的稳定性
与三角形有关的线段
知识回顾
知识回顾
三角形的分类
三角形的高
三角形的中线
三角形的角平分线
在图中的位置
锐角三角形
三条高全在三角形内部
三条中线全在三角形内部
三条角平分线全在三角形内部
直角三角形
一条高位于三角形内部,另外两条高与直角边重合
钝角三角形
一条高位于三角形内部,另外两条高位于三角形
外部
知识回顾
知识回顾
三角形的分类
三角形的高
三角形的中线
三角形的角平分线
交点的
位置
锐角三角形
三条高的交点在三角形内部
三条中线的交点在三角形内部
(重心)
三条角平分线的交点在三角形内部
(内心)
直角三角形
三条高的交点在三角形
直角顶点
钝角三角形
三条高的交点在三角形外部
学习目标
1.了解三角形的稳定性.
2.了解三角形的稳定性和四边形的不稳定性的应用.
3.准确地在生活中使用三角形的稳定性.
课堂导入
盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,如图,大家想一想为什么要这样做呢?
工程建筑中经常采用三角形的结构,如屋顶钢架、房梁,其中的道理是什么呢?
生活小常识
新知探究
动手试一试
(1)把三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
发现:三角形木架的形状不会改变,说明三角形具有稳定性.
新知探究
动手试一试
(2)把四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
发现:四边形木架的形状会改变,说明四边形不具有稳定性,
也即说明四边形具有不稳定性.
新知探究
动手试一试
(3)在(2)的四边形木架上再钉一根木条,将四边形的一对顶点连接起来,然后再扭动它,这时木架的形状还会改变吗?为什么?
发现:钉了一根木条的四边形木架的形状不会改变.
原因:斜钉了一根木条后,四边形变成了两个三角形,由于三角形具有稳定性,所以四边形木架的形状不会改变.
知识点1
新知探究
三角形的稳定性
结论:三角形具有稳定性,四边形具有不稳定性,将不稳定的多边形转化为三角形可以使其具有稳定性.
请尝试列举出生活中应用三角形稳定性的例子?
知识点1
新知探究
请尝试列举出生活中应用四边形不稳定性的例子?
三角形的稳定性
跟踪训练
新知探究
1、下列图形哪些具有稳定性?
有
无
无
有
无
有
跟踪训练
新知探究
2、下列关于三角形的稳定性和四边形的不稳定性,说法正确的是(
)
A.稳定性总是有益的,而不稳定性总是有害的
B.稳定性有利用价值,而不稳定性没有利用价值
C.稳定性和不稳定性均有价值
D.以上说法都不对
C
随堂练习
1、下列具有稳定性的是(
)
A.正方形
B.长方形
C.三角形
D.平行四边形
2、木工师傅做完门框后,常常像右图所示一样钉上两条斜拉的木条,
这样做是因为(
).
3、桥梁的斜拉钢索是三角形的结构,主要是为了(
)
A.节约材料,节约成本
B.保持对称性
C.利用三角形的稳定性
D.美观漂亮
C
三角形具有稳定性
C
随堂练习
4、下列设备中没有利用三角形的稳定性的是(
)
A.索道支架
B.起重机
C.屋顶三角形支架
D.活动的四边形衣架
5、电动伸缩门利用了(
)的性质.
6、下图中不具有稳定性的是(
)
D
四边形的不稳定性
A
B
C
D
B
课堂小结
三角形
四边形
稳定性
不稳定性
稳定性和不稳定性在实际生活中发挥不同的作用
将四边形转化成数个三角形,原来的四边形就具有稳定性了.
拓展提升
1
1、(1)要使四边形木架(用四根木条钉成)具有稳定性,至少要再钉上几根木条?
(2)要使五边形木架(用五根木条钉成)具有稳定性,至少要再钉上几根木条?
(3)要使六边形木架(用六根木条钉成)具有稳定性,至少要再钉上几根木条?
拓展提升
1
1、(1)要使四边形木架(用四根木条钉成)具有稳定性,至少要再钉上几根木条?
(2)要使五边形木架(用五根木条钉成)具有稳定性,至少要再钉上几根木条?
(3)要使六边形木架(用六根木条钉成)具有稳定性,至少要再钉上几根木条?
至少再需要1根木条,使得变成2个三角形.
至少再需要2根木条,使得变成3个三角形.
至少再需要3根木条,使得变成4个三角形.
拓展提升
1
1、(4)要使n边形木架(用n根木条钉成)具有稳定性,至少要再钉上几根木条?
根据四边形木架、五边形木架和六边形木架的规律,n边形木架至少再需要(n-3)根木条,使得变成(n-2)个三角形.
学会用数学归纳法解决第(4)问.
