人教版八年级数学上册11.2.1三角形的内角课件(25张PPT)
文档属性
| 名称 | 人教版八年级数学上册11.2.1三角形的内角课件(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 361.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 07:34:57 | ||
图片预览






文档简介
(共25张PPT)
11.2.1 三角形的内角
与三角形有关的角
知识回顾
1、三角形的概念和表示方法、三角形按角分类和按边分类、三角形的三边关系以及实际应用.
2、三角形的高、中线、角平分线的概念、表示方法和性质,三条高、三条中线、三条角平分线分别在三角形的位置以及它们各自交点分别在三角形的位置.
3、三角形的稳定性以及实际应用.
学习目标
1.学习和掌握三角形的内角和定理.
2.理解三角形的内角和定理的推导、验证过程.
3.在解决实际问题时能熟练运用三角形的内角和定理.
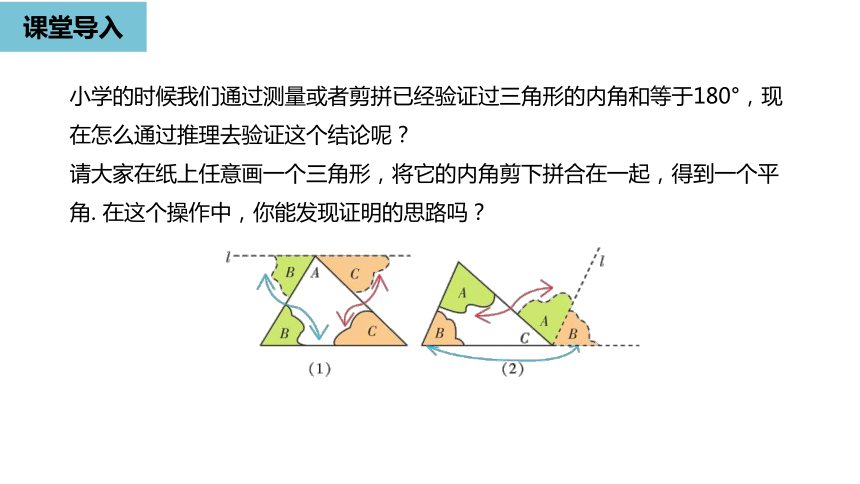
课堂导入
小学的时候我们通过测量或者剪拼已经验证过三角形的内角和等于180°,现在怎么通过推理去验证这个结论呢?
请大家在纸上任意画一个三角形,将它的内角剪下拼合在一起,得到一个平角.
在这个操作中,你能发现证明的思路吗?
知识点1
新知探究
如图,∠B,∠C分别拼凑在∠A的左右两侧,三个角合起来形成一个平角,出现一条过点A的直线l.
想一想,直线l与△ABC的边BC有什么关系?由这个图,你能想出证明“三角形的内角和等于180°”的方法吗?
从位置关系和角度的大小关系可以看出,直线l与边BC是平行关系.
三角形内角和定理
知识点1
新知探究
如图,已知△ABC,求证∠A+∠B+∠C=180°.
证明:过点A作直线l,使得l//BC.
∵l//BC,
∴∠2=∠B,∠3=∠C(两直线平行,内错角相等).
∵∠1、∠2、∠3构成平角,
∴∠1+∠2+∠3=180°(平角的定义).
则∠BAC+∠B+∠C=180°(等量代换).
你能想出来其他的证明方法吗?
三角形内角和定理
A
C
1
2
3
l
B
知识点1
新知探究
证明:过点C作直线l,使得l//AB,延长BC.
∵l//AB,
∴∠2=∠A(两直线平行,内错角相等),
∠3=∠B(两直线平行,同位角相等).
∵∠1、∠2、∠3构成平角,
∴∠1+∠2+∠3=180°(平角的定义).
则∠ACB+∠A+∠B=180°(等量代换).
三角形内角和定理:三角形三个内角的和为180°.
三角形内角和定理
如图,已知△ABC,求证∠A+∠B+∠C=180°.
A
C
1
2
3
l
B
例题讲解
新知探究
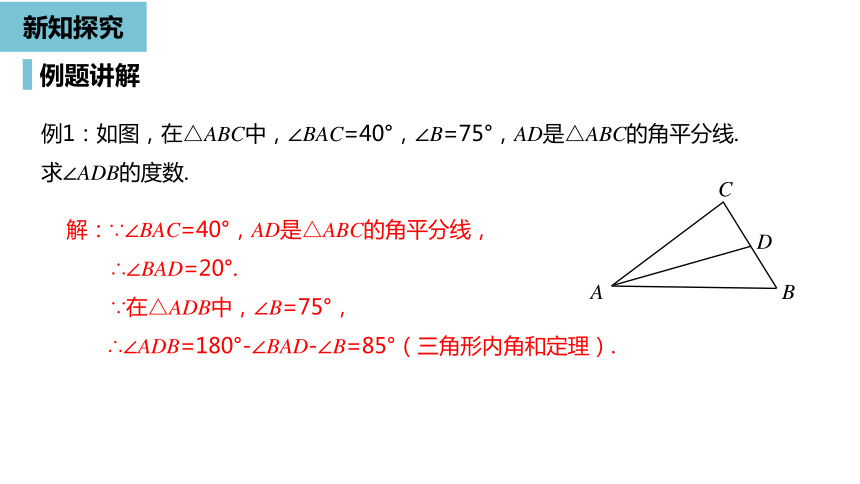
例1:如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线.
求∠ADB的度数.
解:∵∠BAC=40°,AD是△ABC的角平分线,
∴∠BAD=20°.
∵在△ADB中,∠B=75°,
∴∠ADB=180°-∠BAD-∠B=85°(三角形内角和定理).
A
D
C
B
例题讲解
新知探究
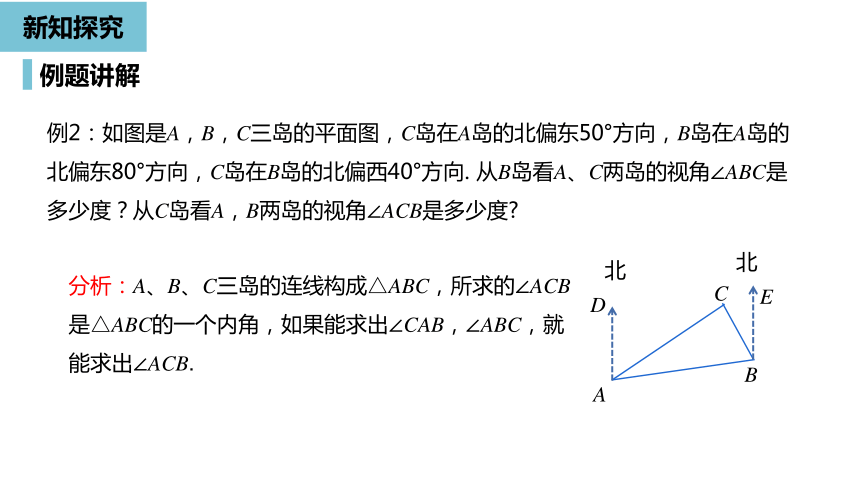
例2:如图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向.
从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A,B两岛的视角∠ACB是多少度?
A
B
C
D
北
北
分析:A、B、C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角,如果能求出∠CAB,∠ABC,就能求出∠ACB.
E
例题讲解
新知探究
解:∠CAB=∠BAD-∠CAD=80°-50°=30°,
由AD//BE得,∠BAD+∠ABE=180°,
所以∠ABE=180°-∠BAD=180°-80°=100°,
∠ABC=∠ABE-∠EBC=100°-40°=60°.
在△ABC中,∠ACB=180°-∠ABC-∠CAB
=180°-60°-30°
=90°.
答:从B岛看A,C两岛的视角∠ABC是60度,从C岛看A,B两岛的视角∠ACB是90度.
A
B
C
D
北
北
E
跟踪训练
新知探究
1、如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A,B两处的视角∠ACB是多少度?
┐
A
B
D
C
解:∵∠CAD=30°,∠ADC=90°,
∴∠ACD=60°.
∵∠CBD=45°,∠ADC=90°,
∴∠BCD=45°.
∴∠ACB=∠ACD-∠BCD=15°.
解:∠A+∠B=90°.
∵在直角三角形ABC中,∠C=90°,
∠A+∠B+∠C=180°,则∠A+∠B=180°-∠C.
∴∠A+∠B=90°.
知识点2
新知探究
在直角三角形ABC中,∠C=90°,两个锐角有什么关系?
C
B
A
┐
直角三角形的性质与判定
知识点2
新知探究
性质:直角三角形的两个锐角互余.
几何语言:在△ABC中,如果∠C=90°,那么∠A+∠B=90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,即直角三角形ABC可以写成Rt△ABC.
注意:Rt△后必须紧跟表示直角三角形的三个顶点的大写字母,不能单独使用.
直角三角形的性质与判定
例题解析
新知探究
如图,∠C=∠D=90°,AD,BC相交于点E,∠CAE与∠DBE有什么关系?为什么?
解:在Rt△ACE中,∠CAE=90°-∠AEC,
在Rt△BDE中,∠DBE=90°-∠BED.
∵∠AEC=∠BED,
∴∠CAE=∠DBE.
A
B
C
D
E
知识点2
新知探究
判定:有两个角互余的三角形是直角三角形.
几何语言:在△ABC中,如果∠A+∠B=90°,那么△ABC是直角三角形.
注意:在直角三角形中,若已知一个锐角或者两个锐角之间的关系,可以直接运用两个锐角互余求解,不需要再利用三角形的内角和定理求解.
直角三角形的性质与判定
跟踪训练
新知探究
1、如图,∠ACB=90°,CD⊥AB,垂足为D,∠ACD与∠B有什么关系?为什么?
A
D
B
C
解:∠ACD与∠B大小相等.
在△BCD中,CD⊥AB,
则∠CDB=90°,∠B+∠BCD=90°.
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,则∠ACD=∠B.
┌
跟踪训练
新知探究
2、如图,∠C=90°,∠1=∠2,△ADE是直角三角形吗?为什么?
A
C
E
B
D
1
2
解:△ADE是直角三角形.
∵在△ABC中,∠C=90°,
∴∠A+∠2=90°.
∵∠1=∠2,
∴∠A+∠1=90°,则△ADE是直角三角形.
随堂练习
1
如图,在△ABC中,AD是BC边上的高,点E是AB边上的一点,CE交AD于点M,且∠DCM=∠MAE.
求证:△ACE是直角三角形.
证明:∵AD是BC边上的高,
∴∠DMC+∠DCM=90°.
∵∠DMC=∠AME,∠DCM=∠MAE,
∴∠AME+∠MAE=90°.
∴△ACE是直角三角形.
A
B
C
D
E
M
┌
随堂练习
2
如图,在△ABC中,AD⊥BC,∠1=∠B.
求证:△ABC是直角三角形.
证明:∵AD⊥BC,
∴∠BAD+∠B=90°.
∵∠1=∠B,
∴∠BAD+∠1=90°,则∠BAC=90°.
∴△ABC是直角三角形.
A
B
D
C
1
随堂练习
3
如图,AB//CD,∠BAE=∠DCE=45°,填空:
∵AB//CD,
∴∠1+45°+∠2+45°=(
).
∴∠1+∠2=(
).
∴∠E=(
).
∴△AEC是(
).
A
B
D
C
E
1
2
45°
45°
180°
90°
90°
直角三角形
课堂小结
三角形的
内角
三角形内角和定理
直角三角形的性质
直角三角形的判定
有两个角互余的三角形是直角三角形
三角形的内角和为180°
直角三角形的
两个锐角互余
拓展提升
1
如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE//BC交AC于点E,若∠A=54°,∠B=48°,则∠CDE的大小是(
)
A.44°
B.40°
C.39°
D.38°
E
A
C
B
D
分析:利用三角形内角和定理,可以求出△ABC的
第三个内角的度数.
利用角平分线的性质和平行线的性质,可以
转化出相等的角.
拓展提升
1
解:∵∠A=54°,∠B=48°,
∴∠ACB=180°-54°-48°=78°.
∵CD平分∠ACB,
∴∠DCB=39°.
∵DE//BC,
∴∠CDE=∠DCB=39°.
如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE//BC交AC于点E,若∠A=54°,∠B=48°,则∠CDE的大小是(
)
A.44°
B.40°
C.39°
D.38°
C
A
C
B
D
E
拓展提升
2
如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
分析:利用三角形内角和定理,将已知的角度与未知角
之间联系起来.
利用等量代换将相等的角进行替换.
A
C
B
D
1
2
3
4
拓展提升
2
解:∵∠3+∠ADB=180°,∠1+∠2+∠ADB=180°,
∴∠3=∠1+∠2.
∵∠3=∠4,∠1=∠2,
∴∠4=∠1+∠2=2∠1.
∵∠1+∠2+∠4+∠DAC=180°,
∴∠DAC=180°-∠1-∠2-∠4=180°-4∠1.
∵∠BAC=∠1+∠DAC=∠1+(180°-4∠1)=180°-3∠1=63°,
∴∠1=39°,则∠DAC=24°.
A
C
B
D
1
2
3
4
如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
11.2.1 三角形的内角
与三角形有关的角
知识回顾
1、三角形的概念和表示方法、三角形按角分类和按边分类、三角形的三边关系以及实际应用.
2、三角形的高、中线、角平分线的概念、表示方法和性质,三条高、三条中线、三条角平分线分别在三角形的位置以及它们各自交点分别在三角形的位置.
3、三角形的稳定性以及实际应用.
学习目标
1.学习和掌握三角形的内角和定理.
2.理解三角形的内角和定理的推导、验证过程.
3.在解决实际问题时能熟练运用三角形的内角和定理.
课堂导入
小学的时候我们通过测量或者剪拼已经验证过三角形的内角和等于180°,现在怎么通过推理去验证这个结论呢?
请大家在纸上任意画一个三角形,将它的内角剪下拼合在一起,得到一个平角.
在这个操作中,你能发现证明的思路吗?
知识点1
新知探究
如图,∠B,∠C分别拼凑在∠A的左右两侧,三个角合起来形成一个平角,出现一条过点A的直线l.
想一想,直线l与△ABC的边BC有什么关系?由这个图,你能想出证明“三角形的内角和等于180°”的方法吗?
从位置关系和角度的大小关系可以看出,直线l与边BC是平行关系.
三角形内角和定理
知识点1
新知探究
如图,已知△ABC,求证∠A+∠B+∠C=180°.
证明:过点A作直线l,使得l//BC.
∵l//BC,
∴∠2=∠B,∠3=∠C(两直线平行,内错角相等).
∵∠1、∠2、∠3构成平角,
∴∠1+∠2+∠3=180°(平角的定义).
则∠BAC+∠B+∠C=180°(等量代换).
你能想出来其他的证明方法吗?
三角形内角和定理
A
C
1
2
3
l
B
知识点1
新知探究
证明:过点C作直线l,使得l//AB,延长BC.
∵l//AB,
∴∠2=∠A(两直线平行,内错角相等),
∠3=∠B(两直线平行,同位角相等).
∵∠1、∠2、∠3构成平角,
∴∠1+∠2+∠3=180°(平角的定义).
则∠ACB+∠A+∠B=180°(等量代换).
三角形内角和定理:三角形三个内角的和为180°.
三角形内角和定理
如图,已知△ABC,求证∠A+∠B+∠C=180°.
A
C
1
2
3
l
B
例题讲解
新知探究
例1:如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线.
求∠ADB的度数.
解:∵∠BAC=40°,AD是△ABC的角平分线,
∴∠BAD=20°.
∵在△ADB中,∠B=75°,
∴∠ADB=180°-∠BAD-∠B=85°(三角形内角和定理).
A
D
C
B
例题讲解
新知探究
例2:如图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向.
从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A,B两岛的视角∠ACB是多少度?
A
B
C
D
北
北
分析:A、B、C三岛的连线构成△ABC,所求的∠ACB是△ABC的一个内角,如果能求出∠CAB,∠ABC,就能求出∠ACB.
E
例题讲解
新知探究
解:∠CAB=∠BAD-∠CAD=80°-50°=30°,
由AD//BE得,∠BAD+∠ABE=180°,
所以∠ABE=180°-∠BAD=180°-80°=100°,
∠ABC=∠ABE-∠EBC=100°-40°=60°.
在△ABC中,∠ACB=180°-∠ABC-∠CAB
=180°-60°-30°
=90°.
答:从B岛看A,C两岛的视角∠ABC是60度,从C岛看A,B两岛的视角∠ACB是90度.
A
B
C
D
北
北
E
跟踪训练
新知探究
1、如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A,B两处的视角∠ACB是多少度?
┐
A
B
D
C
解:∵∠CAD=30°,∠ADC=90°,
∴∠ACD=60°.
∵∠CBD=45°,∠ADC=90°,
∴∠BCD=45°.
∴∠ACB=∠ACD-∠BCD=15°.
解:∠A+∠B=90°.
∵在直角三角形ABC中,∠C=90°,
∠A+∠B+∠C=180°,则∠A+∠B=180°-∠C.
∴∠A+∠B=90°.
知识点2
新知探究
在直角三角形ABC中,∠C=90°,两个锐角有什么关系?
C
B
A
┐
直角三角形的性质与判定
知识点2
新知探究
性质:直角三角形的两个锐角互余.
几何语言:在△ABC中,如果∠C=90°,那么∠A+∠B=90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,即直角三角形ABC可以写成Rt△ABC.
注意:Rt△后必须紧跟表示直角三角形的三个顶点的大写字母,不能单独使用.
直角三角形的性质与判定
例题解析
新知探究
如图,∠C=∠D=90°,AD,BC相交于点E,∠CAE与∠DBE有什么关系?为什么?
解:在Rt△ACE中,∠CAE=90°-∠AEC,
在Rt△BDE中,∠DBE=90°-∠BED.
∵∠AEC=∠BED,
∴∠CAE=∠DBE.
A
B
C
D
E
知识点2
新知探究
判定:有两个角互余的三角形是直角三角形.
几何语言:在△ABC中,如果∠A+∠B=90°,那么△ABC是直角三角形.
注意:在直角三角形中,若已知一个锐角或者两个锐角之间的关系,可以直接运用两个锐角互余求解,不需要再利用三角形的内角和定理求解.
直角三角形的性质与判定
跟踪训练
新知探究
1、如图,∠ACB=90°,CD⊥AB,垂足为D,∠ACD与∠B有什么关系?为什么?
A
D
B
C
解:∠ACD与∠B大小相等.
在△BCD中,CD⊥AB,
则∠CDB=90°,∠B+∠BCD=90°.
∵∠ACB=90°,
∴∠ACD+∠BCD=90°,则∠ACD=∠B.
┌
跟踪训练
新知探究
2、如图,∠C=90°,∠1=∠2,△ADE是直角三角形吗?为什么?
A
C
E
B
D
1
2
解:△ADE是直角三角形.
∵在△ABC中,∠C=90°,
∴∠A+∠2=90°.
∵∠1=∠2,
∴∠A+∠1=90°,则△ADE是直角三角形.
随堂练习
1
如图,在△ABC中,AD是BC边上的高,点E是AB边上的一点,CE交AD于点M,且∠DCM=∠MAE.
求证:△ACE是直角三角形.
证明:∵AD是BC边上的高,
∴∠DMC+∠DCM=90°.
∵∠DMC=∠AME,∠DCM=∠MAE,
∴∠AME+∠MAE=90°.
∴△ACE是直角三角形.
A
B
C
D
E
M
┌
随堂练习
2
如图,在△ABC中,AD⊥BC,∠1=∠B.
求证:△ABC是直角三角形.
证明:∵AD⊥BC,
∴∠BAD+∠B=90°.
∵∠1=∠B,
∴∠BAD+∠1=90°,则∠BAC=90°.
∴△ABC是直角三角形.
A
B
D
C
1
随堂练习
3
如图,AB//CD,∠BAE=∠DCE=45°,填空:
∵AB//CD,
∴∠1+45°+∠2+45°=(
).
∴∠1+∠2=(
).
∴∠E=(
).
∴△AEC是(
).
A
B
D
C
E
1
2
45°
45°
180°
90°
90°
直角三角形
课堂小结
三角形的
内角
三角形内角和定理
直角三角形的性质
直角三角形的判定
有两个角互余的三角形是直角三角形
三角形的内角和为180°
直角三角形的
两个锐角互余
拓展提升
1
如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE//BC交AC于点E,若∠A=54°,∠B=48°,则∠CDE的大小是(
)
A.44°
B.40°
C.39°
D.38°
E
A
C
B
D
分析:利用三角形内角和定理,可以求出△ABC的
第三个内角的度数.
利用角平分线的性质和平行线的性质,可以
转化出相等的角.
拓展提升
1
解:∵∠A=54°,∠B=48°,
∴∠ACB=180°-54°-48°=78°.
∵CD平分∠ACB,
∴∠DCB=39°.
∵DE//BC,
∴∠CDE=∠DCB=39°.
如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE//BC交AC于点E,若∠A=54°,∠B=48°,则∠CDE的大小是(
)
A.44°
B.40°
C.39°
D.38°
C
A
C
B
D
E
拓展提升
2
如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
分析:利用三角形内角和定理,将已知的角度与未知角
之间联系起来.
利用等量代换将相等的角进行替换.
A
C
B
D
1
2
3
4
拓展提升
2
解:∵∠3+∠ADB=180°,∠1+∠2+∠ADB=180°,
∴∠3=∠1+∠2.
∵∠3=∠4,∠1=∠2,
∴∠4=∠1+∠2=2∠1.
∵∠1+∠2+∠4+∠DAC=180°,
∴∠DAC=180°-∠1-∠2-∠4=180°-4∠1.
∵∠BAC=∠1+∠DAC=∠1+(180°-4∠1)=180°-3∠1=63°,
∴∠1=39°,则∠DAC=24°.
A
C
B
D
1
2
3
4
如图,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,求∠DAC的度数.
