人教A版必修2 3.1.2两条直线平行与垂直的判定(共16张PPT)
文档属性
| 名称 | 人教A版必修2 3.1.2两条直线平行与垂直的判定(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 06:30:23 | ||
图片预览






文档简介
(共16张PPT)
3.1.2两条直线平行与垂直的判定
人教A版必修2
重温经典
1.倾斜角
2.斜率及斜率公式
3.求经过A(-2,0),B(-5,3)两点的直线的AB斜率和倾斜角.
4.在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线
。
O
x
y
A3
A1
A2
A4
重温经典
深入思考
1.能否通过直线的斜率,来判断两条直线的位置关系呢?
2.如果两条直线平行,斜率具有什么样的关系呢?
1
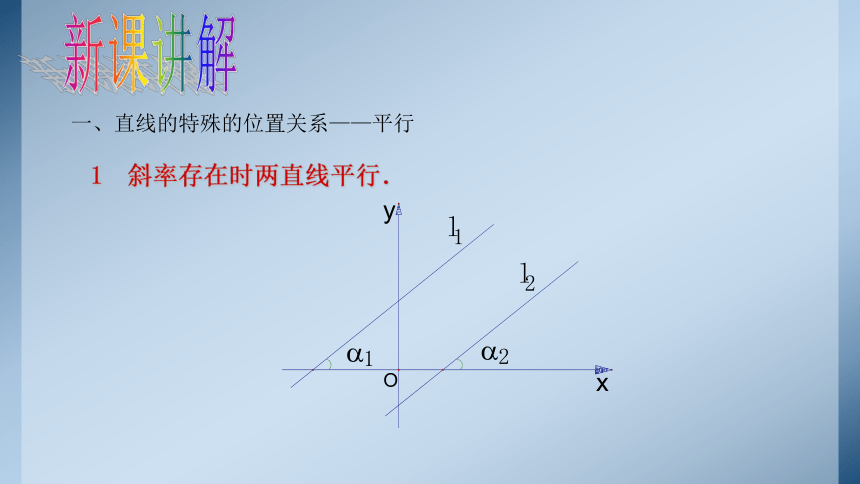
斜率存在时两直线平行.
新课讲解
一、直线的特殊的位置关系——平行
结论1:
如果直线L1,L2的斜率为k1,k2;那么
L1∥L2
?
k1=k2
注意:上面的等价是在两直线斜率存在的前提下才成立的,
缺少这个前提,结论并不存立.
新课讲解
一、直线的特殊的位置关系——平行
新课讲解
2.如果斜率不存在,又是什么情况呢?
两直线的倾斜角都为90°,互相平行.
一、直线的特殊的位置关系——平行
例1、已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论。
例2、已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
课堂活动
1.设两条直线l1、l2的倾斜角分别为α1、α2(
α1、α2≠90°).
二、直线的特殊的位置关系——垂直
新课讲解
结论2:如果两条直线l1、l2都有斜率,且分别为k1、k2,则有
l1⊥l2
k1k2=-1.
二、直线的特殊的位置关系——垂直
新课讲解
思考:上面结论的成立条件是什么呢?
2.特殊情况下
当两条直线中有一条直线没有斜率时:
则一条直线的倾斜角为900,另一条直线的倾斜角为0°
两直线互相垂直
二、直线的特殊的位置关系——垂直
新课讲解
例3、已知A(-6,0),B(3,6),P(0,3)Q(6,6),判断直线AB与PQ的位置关系。
课堂活动
参与进来!
2.已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状。
1.已知直线
l1
过点
A(3,a),B(a-1,4),直线
l2
过点
C(1,2),
D(-2,a+2).
(1)若
l1∥l2,求
a
的值;
(2)若
l1⊥l2,求
a
的值.
两直线平行
1.如果
l1∥l2,则
k1=k2
且
b1≠b2;如果
k1=k2
且
b1≠b2,则
l1∥l2.
2.当
l1
与
l2
的斜率都不存在且
l1
与
l2
不重合时,则
l1
与
l2平行.
回顾总结
两直线垂直
当
l1⊥l2
时,它们的斜率之间的关系有两种情况:
3.它们的斜率都存在且
k1k2=-1;
4.一条直线的斜率不存在,而另一条直线的斜率为
0.
已知直线
l1:y=k1x+b1
,
l2:y=k2x+b2,
已知直线
与
互相垂直,求?的值
0
2
)
3
2
(
)
1
(
=
+
+
+
-
y
a
x
a
0
3
)
1
(
)
2
(
=
-
-
+
+
y
a
x
a
课后思考!
实践活动
作业布置:校本作业《直线的平行与垂直》
3.1.2两条直线平行与垂直的判定
人教A版必修2
重温经典
1.倾斜角
2.斜率及斜率公式
3.求经过A(-2,0),B(-5,3)两点的直线的AB斜率和倾斜角.
4.在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线
。
O
x
y
A3
A1
A2
A4
重温经典
深入思考
1.能否通过直线的斜率,来判断两条直线的位置关系呢?
2.如果两条直线平行,斜率具有什么样的关系呢?
1
斜率存在时两直线平行.
新课讲解
一、直线的特殊的位置关系——平行
结论1:
如果直线L1,L2的斜率为k1,k2;那么
L1∥L2
?
k1=k2
注意:上面的等价是在两直线斜率存在的前提下才成立的,
缺少这个前提,结论并不存立.
新课讲解
一、直线的特殊的位置关系——平行
新课讲解
2.如果斜率不存在,又是什么情况呢?
两直线的倾斜角都为90°,互相平行.
一、直线的特殊的位置关系——平行
例1、已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),试判断直线BA与PQ的位置关系,并证明你的结论。
例2、已知四边形ABCD的四个顶点分别为A(0,0),B(2,-1),C(4,2),D(2,3),试判断四边形ABCD的形状,并给出证明。
课堂活动
1.设两条直线l1、l2的倾斜角分别为α1、α2(
α1、α2≠90°).
二、直线的特殊的位置关系——垂直
新课讲解
结论2:如果两条直线l1、l2都有斜率,且分别为k1、k2,则有
l1⊥l2
k1k2=-1.
二、直线的特殊的位置关系——垂直
新课讲解
思考:上面结论的成立条件是什么呢?
2.特殊情况下
当两条直线中有一条直线没有斜率时:
则一条直线的倾斜角为900,另一条直线的倾斜角为0°
两直线互相垂直
二、直线的特殊的位置关系——垂直
新课讲解
例3、已知A(-6,0),B(3,6),P(0,3)Q(6,6),判断直线AB与PQ的位置关系。
课堂活动
参与进来!
2.已知A(5,-1),B(1,1),C(2,3)三点,试判断△ABC的形状。
1.已知直线
l1
过点
A(3,a),B(a-1,4),直线
l2
过点
C(1,2),
D(-2,a+2).
(1)若
l1∥l2,求
a
的值;
(2)若
l1⊥l2,求
a
的值.
两直线平行
1.如果
l1∥l2,则
k1=k2
且
b1≠b2;如果
k1=k2
且
b1≠b2,则
l1∥l2.
2.当
l1
与
l2
的斜率都不存在且
l1
与
l2
不重合时,则
l1
与
l2平行.
回顾总结
两直线垂直
当
l1⊥l2
时,它们的斜率之间的关系有两种情况:
3.它们的斜率都存在且
k1k2=-1;
4.一条直线的斜率不存在,而另一条直线的斜率为
0.
已知直线
l1:y=k1x+b1
,
l2:y=k2x+b2,
已知直线
与
互相垂直,求?的值
0
2
)
3
2
(
)
1
(
=
+
+
+
-
y
a
x
a
0
3
)
1
(
)
2
(
=
-
-
+
+
y
a
x
a
课后思考!
实践活动
作业布置:校本作业《直线的平行与垂直》
