人教版八年级数学上册12.2三角形全等的判定课时3课件(23张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.2三角形全等的判定课时3课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 180.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
12.2.3 三角形全等的判定
全等三角形的判定
知识回顾
1、什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
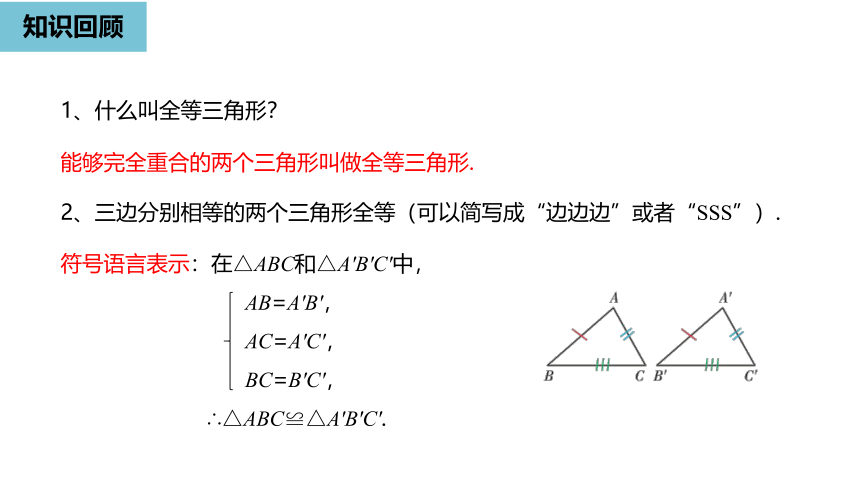
2、三边分别相等的两个三角形全等(可以简写成“边边边”或者“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C'.
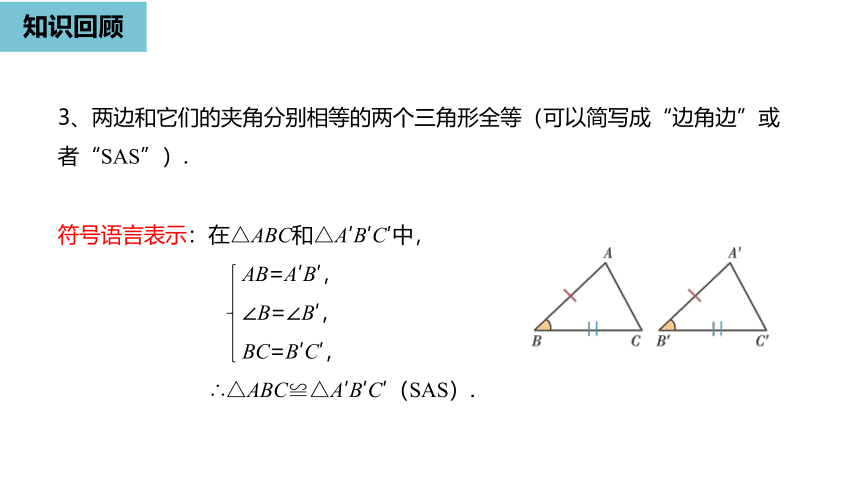
3、两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或者“SAS”).
符号语言表示:在△ABC和△A′B′C′中,
AB=A′B′,
∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′(SAS).
知识回顾
学习目标
1、理解并掌握三角形全等判定“角边角”条件的内容.
2、熟练利用“角边角”条件证明两个三角形全等.
3、通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
课堂导入
先任意画出一个△ABC,再画一个△A′B′C′,使得AB=A′B′,∠A=∠A′,∠B=∠B′(即两角和它们的夹边分别相等).此时的△ABC和△A′B′C′全等吗?
画法:1、画A′B′=AB.
2、在A′B′的同旁画∠DA′B′=∠A,∠EB′A′=∠B,
A′D,B′E相交于点C′.
3、△A′B′C′即为所作三角形.
课堂导入
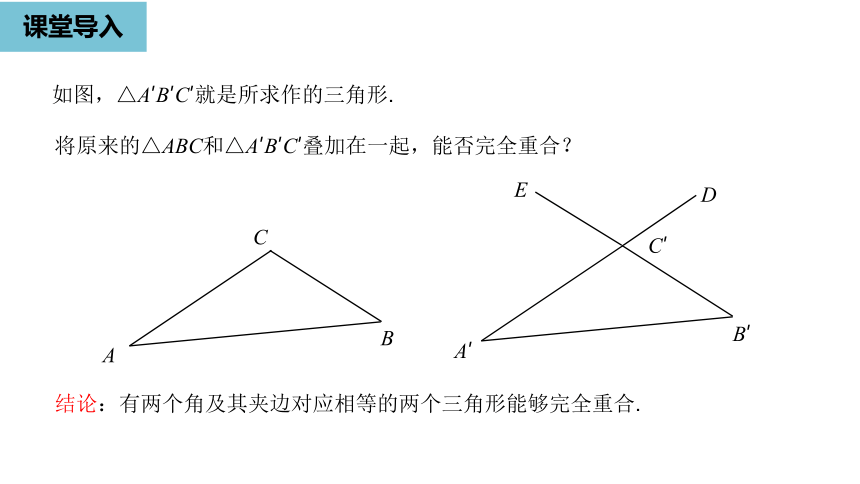
如图,△A′B′C′就是所求作的三角形.
将原来的△ABC和△A′B′C′叠加在一起,能否完全重合?
结论:有两个角及其夹边对应相等的两个三角形能够完全重合.
C
A
B
C′
A′
B′
E
D
知识点1
新知探究
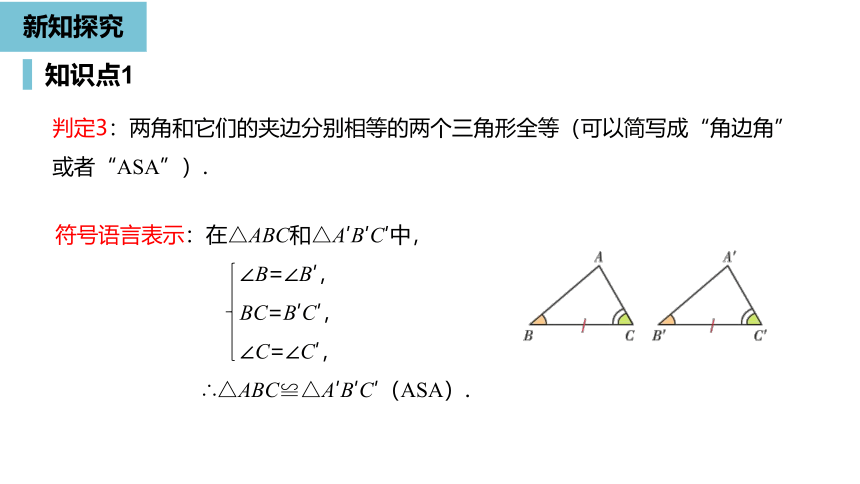
判定3:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”).
符号语言表示:在△ABC和△A′B′C′中,
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(ASA).
例题解析
新知探究
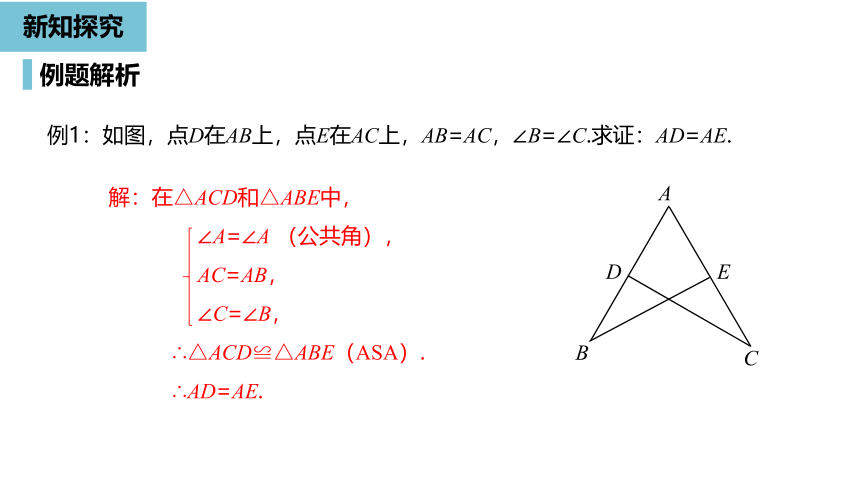
例1:如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
解:在△ACD和△ABE中,
∠A=∠A
(公共角),
AC=AB,
∠C=∠B,
∴△ACD≌△ABE(ASA).
∴AD=AE.
D
E
B
C
A
例题解析
新知探究
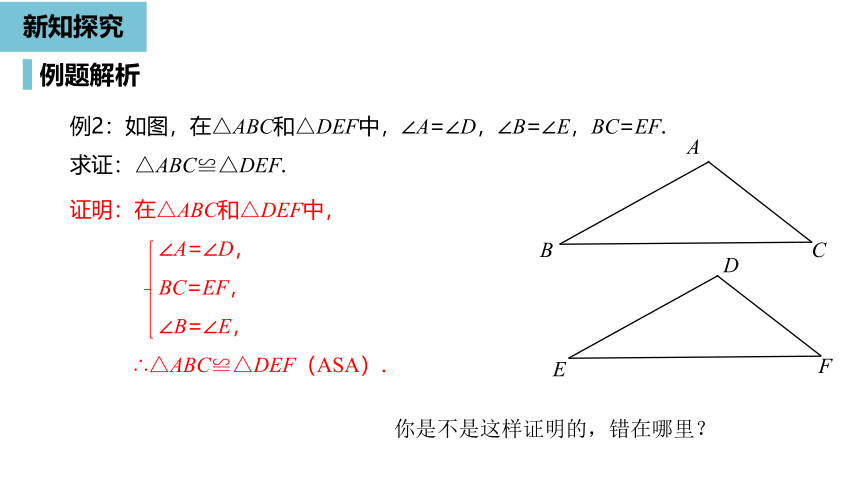
例2:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:在△ABC和△DEF中,
∠A=∠D,
BC=EF,
∠B=∠E,
∴△ABC≌△DEF(ASA).
你是不是这样证明的,错在哪里?
A
B
E
D
C
F
例题解析
新知探究
分析:BC,EF不是已知两对角的夹边,在
三角形中,知道两个角的关系,利用三角
形内角和定理可以求得第三个角之间的关
系.通过转化来构造“ASA”的判定条件.
A
B
E
D
C
F
例2:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
例题解析
新知探究
证明:在△ABC和△DEF中,
∵∠A=∠D,∠B=∠E,
∠C=180°-∠A-∠B,∠F=180°-∠D-∠E,
∴∠C=∠F.
在△ABC和△DEF中,
∠B=∠E,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF(ASA).
A
B
E
D
C
F
跟踪训练
新知探究
如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.
求证:AB=AD.
分析:图中的两个三角形有公共边AC,有一对角
相等可以选择“SAS”或者“ASA”.根据题意,有
AB⊥BC,AD⊥DC,则构成∠ABC=∠ADC=90°.
可以选择“ASA”,需要将已知角转化成两角及其
夹边,即可求证.
A
B
C
D
1
2
跟踪训练
新知探究
证明:∵AB⊥BC,AD⊥DC,
∴∠ABC=∠ADC=90°.
∵在△ABC和△ADC中,∠1=∠2,∠ABC=∠ADC,
∴∠ACB=∠ACD.
在△ABC和△ADC中,
∠1=∠2,
AC=AC(公共边),
∠ACB=∠ACD,
∴△ABC≌△ADC(ASA),
∴AB=AD.
A
B
C
D
1
2
如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.
求证:AB=AD.
跟踪训练
新知探究
如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使得BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
A
B
C
D
F
E
┐
┐
分析:根据题意构造出两个直角三角形,利用
全等三角形的性质得出对应边相等.注意题目
中隐藏一对对顶角,根据“ASA”证明两个三角
形全等即可得出题目要求的结论.
跟踪训练
新知探究
解:由题可知:AB⊥BC,ED⊥DC,
则∠ABC=∠EDC=90°.
在△ABC和△EDC中,
∠ABC=∠EDC,
BC=DC,
∠ACB=∠ECD,
∴△ABC≌△EDC(ASA).
∴AB=ED,则DE的长就是AB的长.
A
B
C
D
F
E
┐
┐
随堂练习
1
如下图,已知∠B=∠D,DC=BC,还需要给出什么条件,即可用学过的判定得出△ABC≌△EDC.根据哪个判定?
条件(
),根据(
).
条件(
),根据(
).
AB=ED
∠ACB=∠ECD
两边及其夹角分别相等的两个三角形全等
两角及其夹边分别相等的两个三角形全等
C
E
A
D
B
随堂练习
2
如图,已知∠1=∠2,∠C=∠D.求证:AC=AD.
证明:∵∠1=∠2,∠C=∠D,
∴∠ABC=∠ABD
(三角形内角和定理).
在△ABC和△ABD中,
∠1=∠2,
AB=AB(公共边),
∠ABC=∠ABD,
∴△ABC≌△ABD(ASA).
∴AC=AD.
A
B
1
2
C
D
随堂练习
3
如图,已知D是AC上一点,AB=DA,DE//AB,∠B=∠DAE.
求证:△ABC≌△DAE.
证明:∵DE//AB,
∴
∠CAB=∠EDA.
在△ABC和△DAE中,
∠CAB=∠EDA,
AB=DA,
∠B=∠DAE,
∴△ABC≌△DAE(ASA).
为你支招:有平行线就可以转化出相等的角.
随堂练习
4
如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,如果EF=5cm,那么AE=(
)cm.
分析:题目中已经给出一对边相等,可以选择“SSS”,“SAS”或者“ASA”.根据题意的垂直关系可以转化出相等的角,所以本题选择“ASA”.
利用好垂直关系和余角定理是解决本题的关键.
随堂练习
4
解:∵CD⊥AB,
∴∠A+∠ACD=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∴∠B=∠ACD.
∵EF⊥AC,
∴∠FEC=90°.
∴∠ACB=∠FEC.
在△ACB和△FEC中,∠B=∠FCE,
BC=CE,
∠ACB=∠FEC,
∴△ACB≌△FEC(ASA).
∴
AC=EF.
∵BC=2cm,EF=5cm.
∴
AE=3cm.
如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,如果EF=5cm,那么AE=(
)cm.
3
三角形全等的判定
分类
探讨
ASA
应用
两角及其夹边分别相等
两角及其中一角的对边分别相等
两角和它们的夹边分别相等的两个三角形全等
利用“ASA”解决实际问题
课堂小结
拓展提升
1
分析:等角加等角,其和仍然是等角;同理,等角减等角,其差仍然是等角.利用题目中已经给出的角转化出新的相等的角,从而证明三角形全等,利用全等的性质得出对应角相等,对应边相等.
C
1
B
E
D
A
2
如图,已知∠1=∠2,∠E=∠C,AC=AE.求证:AB=AD,∠B=∠D.
拓展提升
1
证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∠BAC=∠DAE,
AC=AE,
∠C=∠E,
∴△ABC≌△ADE(ASA).
∴AB=AD,∠B=∠D.
1
B
E
D
A
2
如图,已知∠1=∠2,∠E=∠C,AC=AE.求证:AB=AD,∠B=∠D.
12.2.3 三角形全等的判定
全等三角形的判定
知识回顾
1、什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
2、三边分别相等的两个三角形全等(可以简写成“边边边”或者“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C'.
3、两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或者“SAS”).
符号语言表示:在△ABC和△A′B′C′中,
AB=A′B′,
∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′(SAS).
知识回顾
学习目标
1、理解并掌握三角形全等判定“角边角”条件的内容.
2、熟练利用“角边角”条件证明两个三角形全等.
3、通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
课堂导入
先任意画出一个△ABC,再画一个△A′B′C′,使得AB=A′B′,∠A=∠A′,∠B=∠B′(即两角和它们的夹边分别相等).此时的△ABC和△A′B′C′全等吗?
画法:1、画A′B′=AB.
2、在A′B′的同旁画∠DA′B′=∠A,∠EB′A′=∠B,
A′D,B′E相交于点C′.
3、△A′B′C′即为所作三角形.
课堂导入
如图,△A′B′C′就是所求作的三角形.
将原来的△ABC和△A′B′C′叠加在一起,能否完全重合?
结论:有两个角及其夹边对应相等的两个三角形能够完全重合.
C
A
B
C′
A′
B′
E
D
知识点1
新知探究
判定3:两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”).
符号语言表示:在△ABC和△A′B′C′中,
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(ASA).
例题解析
新知探究
例1:如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:AD=AE.
解:在△ACD和△ABE中,
∠A=∠A
(公共角),
AC=AB,
∠C=∠B,
∴△ACD≌△ABE(ASA).
∴AD=AE.
D
E
B
C
A
例题解析
新知探究
例2:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:在△ABC和△DEF中,
∠A=∠D,
BC=EF,
∠B=∠E,
∴△ABC≌△DEF(ASA).
你是不是这样证明的,错在哪里?
A
B
E
D
C
F
例题解析
新知探究
分析:BC,EF不是已知两对角的夹边,在
三角形中,知道两个角的关系,利用三角
形内角和定理可以求得第三个角之间的关
系.通过转化来构造“ASA”的判定条件.
A
B
E
D
C
F
例2:如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
例题解析
新知探究
证明:在△ABC和△DEF中,
∵∠A=∠D,∠B=∠E,
∠C=180°-∠A-∠B,∠F=180°-∠D-∠E,
∴∠C=∠F.
在△ABC和△DEF中,
∠B=∠E,
BC=EF,
∠C=∠F,
∴△ABC≌△DEF(ASA).
A
B
E
D
C
F
跟踪训练
新知探究
如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.
求证:AB=AD.
分析:图中的两个三角形有公共边AC,有一对角
相等可以选择“SAS”或者“ASA”.根据题意,有
AB⊥BC,AD⊥DC,则构成∠ABC=∠ADC=90°.
可以选择“ASA”,需要将已知角转化成两角及其
夹边,即可求证.
A
B
C
D
1
2
跟踪训练
新知探究
证明:∵AB⊥BC,AD⊥DC,
∴∠ABC=∠ADC=90°.
∵在△ABC和△ADC中,∠1=∠2,∠ABC=∠ADC,
∴∠ACB=∠ACD.
在△ABC和△ADC中,
∠1=∠2,
AC=AC(公共边),
∠ACB=∠ACD,
∴△ABC≌△ADC(ASA),
∴AB=AD.
A
B
C
D
1
2
如图,AB⊥BC,AD⊥DC,垂足分别为点B,点D,∠1=∠2.
求证:AB=AD.
跟踪训练
新知探究
如图,要测量池塘两岸相对的两点A,B的距离,可以在池塘外取AB的垂线BF上的两点C,D,使得BC=CD.再画出BF的垂线DE,使得E与A,C在一条直线上,这时测得DE的长就是AB的长,为什么?
A
B
C
D
F
E
┐
┐
分析:根据题意构造出两个直角三角形,利用
全等三角形的性质得出对应边相等.注意题目
中隐藏一对对顶角,根据“ASA”证明两个三角
形全等即可得出题目要求的结论.
跟踪训练
新知探究
解:由题可知:AB⊥BC,ED⊥DC,
则∠ABC=∠EDC=90°.
在△ABC和△EDC中,
∠ABC=∠EDC,
BC=DC,
∠ACB=∠ECD,
∴△ABC≌△EDC(ASA).
∴AB=ED,则DE的长就是AB的长.
A
B
C
D
F
E
┐
┐
随堂练习
1
如下图,已知∠B=∠D,DC=BC,还需要给出什么条件,即可用学过的判定得出△ABC≌△EDC.根据哪个判定?
条件(
),根据(
).
条件(
),根据(
).
AB=ED
∠ACB=∠ECD
两边及其夹角分别相等的两个三角形全等
两角及其夹边分别相等的两个三角形全等
C
E
A
D
B
随堂练习
2
如图,已知∠1=∠2,∠C=∠D.求证:AC=AD.
证明:∵∠1=∠2,∠C=∠D,
∴∠ABC=∠ABD
(三角形内角和定理).
在△ABC和△ABD中,
∠1=∠2,
AB=AB(公共边),
∠ABC=∠ABD,
∴△ABC≌△ABD(ASA).
∴AC=AD.
A
B
1
2
C
D
随堂练习
3
如图,已知D是AC上一点,AB=DA,DE//AB,∠B=∠DAE.
求证:△ABC≌△DAE.
证明:∵DE//AB,
∴
∠CAB=∠EDA.
在△ABC和△DAE中,
∠CAB=∠EDA,
AB=DA,
∠B=∠DAE,
∴△ABC≌△DAE(ASA).
为你支招:有平行线就可以转化出相等的角.
随堂练习
4
如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,如果EF=5cm,那么AE=(
)cm.
分析:题目中已经给出一对边相等,可以选择“SSS”,“SAS”或者“ASA”.根据题意的垂直关系可以转化出相等的角,所以本题选择“ASA”.
利用好垂直关系和余角定理是解决本题的关键.
随堂练习
4
解:∵CD⊥AB,
∴∠A+∠ACD=90°.
∵∠ACB=90°,
∴∠A+∠B=90°.
∴∠B=∠ACD.
∵EF⊥AC,
∴∠FEC=90°.
∴∠ACB=∠FEC.
在△ACB和△FEC中,∠B=∠FCE,
BC=CE,
∠ACB=∠FEC,
∴△ACB≌△FEC(ASA).
∴
AC=EF.
∵BC=2cm,EF=5cm.
∴
AE=3cm.
如图,在Rt△ABC中,∠ACB=90°,BC=2cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,如果EF=5cm,那么AE=(
)cm.
3
三角形全等的判定
分类
探讨
ASA
应用
两角及其夹边分别相等
两角及其中一角的对边分别相等
两角和它们的夹边分别相等的两个三角形全等
利用“ASA”解决实际问题
课堂小结
拓展提升
1
分析:等角加等角,其和仍然是等角;同理,等角减等角,其差仍然是等角.利用题目中已经给出的角转化出新的相等的角,从而证明三角形全等,利用全等的性质得出对应角相等,对应边相等.
C
1
B
E
D
A
2
如图,已知∠1=∠2,∠E=∠C,AC=AE.求证:AB=AD,∠B=∠D.
拓展提升
1
证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∠BAC=∠DAE,
AC=AE,
∠C=∠E,
∴△ABC≌△ADE(ASA).
∴AB=AD,∠B=∠D.
1
B
E
D
A
2
如图,已知∠1=∠2,∠E=∠C,AC=AE.求证:AB=AD,∠B=∠D.
