人教版八年级数学上册12.2三角形全等的判定课时4课件(26张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.2三角形全等的判定课时4课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 733.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 00:00:00 | ||
图片预览


文档简介
(共26张PPT)
12.2.4 三角形全等的判定
全等三角形的判定
人教版-数学-八年级上册
知识回顾
1、什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
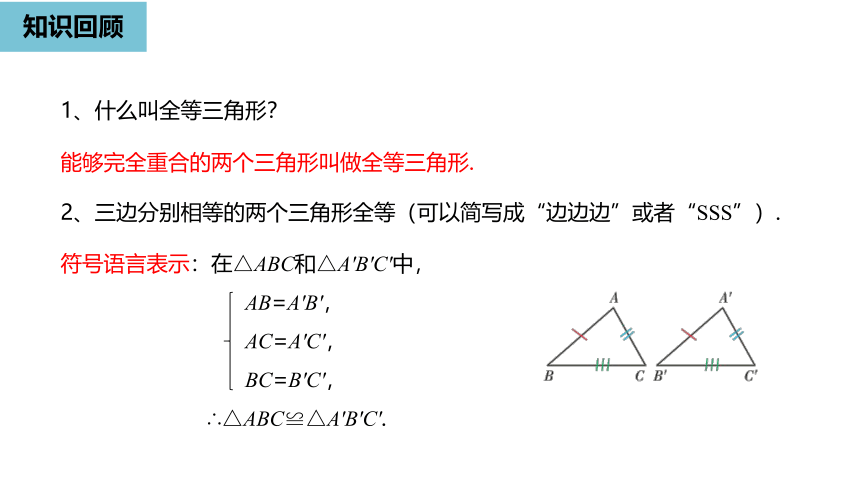
2、三边分别相等的两个三角形全等(可以简写成“边边边”或者“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C'.
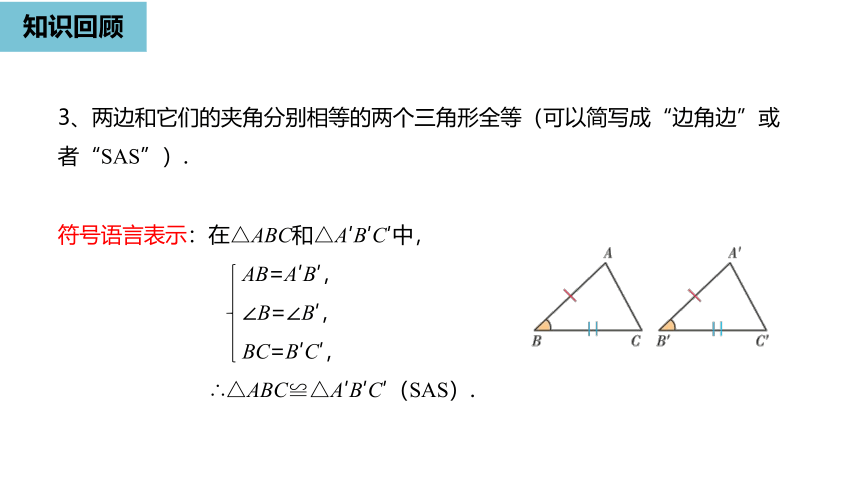
3、两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或者“SAS”).
符号语言表示:在△ABC和△A′B′C′中,
AB=A′B′,
∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′(SAS).
知识回顾
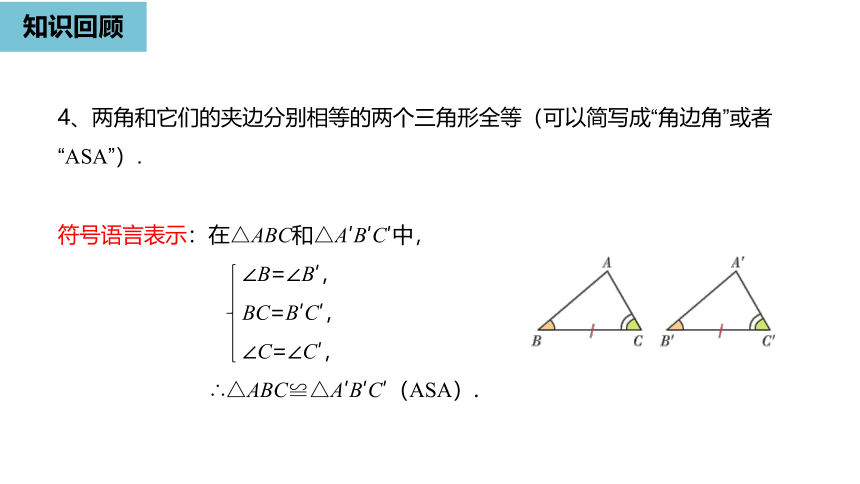
4、两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”).
符号语言表示:在△ABC和△A′B′C′中,
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(ASA).
知识回顾
学习目标
1、理解并掌握三角形全等判定“角角边”条件的内容.
2、熟练利用“角角边”条件证明两个三角形全等.
3、通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
课堂导入
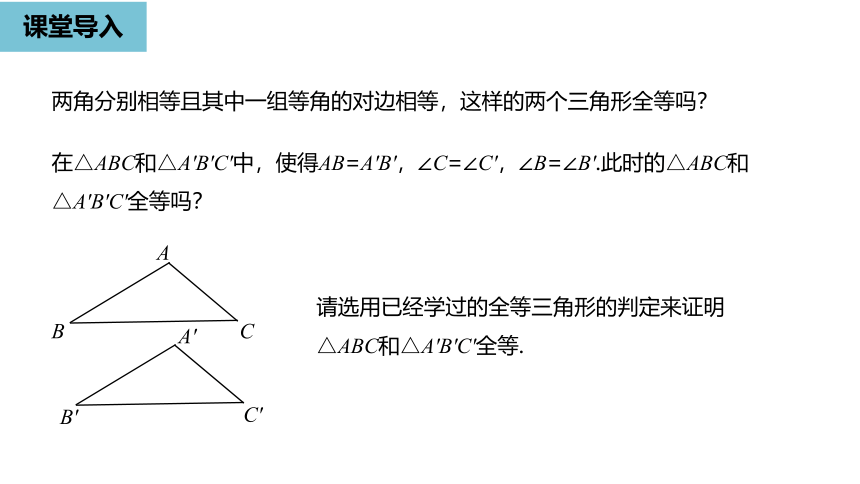
两角分别相等且其中一组等角的对边相等,这样的两个三角形全等吗?
在△ABC和△A'B'C'中,使得AB=A'B',∠C=∠C',∠B=∠B'.此时的△ABC和△A'B'C'全等吗?
请选用已经学过的全等三角形的判定来证明△ABC和△A'B'C'全等.
A
B
B'
A'
C
C'
新知探究
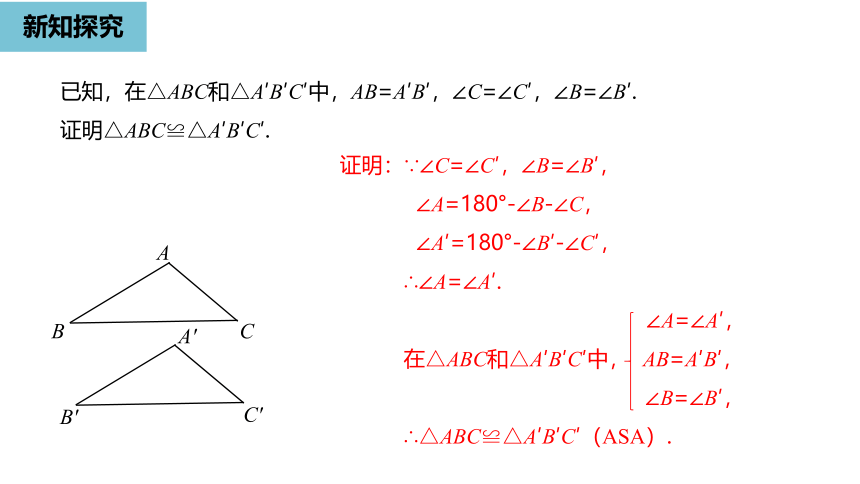
已知,在△ABC和△A′B′C′中,AB=A′B′,∠C=∠C′,∠B=∠B′.
证明△ABC≌△A′B′C′.
证明:∵∠C=∠C′,∠B=∠B′,
∠A=180°-∠B-∠C,
∠A′=180°-∠B′-∠C′,
∴∠A=∠A′.
∠A=∠A′,
在△ABC和△A′B′C′中,
AB=A′B′,
∠B=∠B′,
∴△ABC≌△A′B′C′(ASA).
A
B
B'
A'
C
C'
知识点1
新知探究
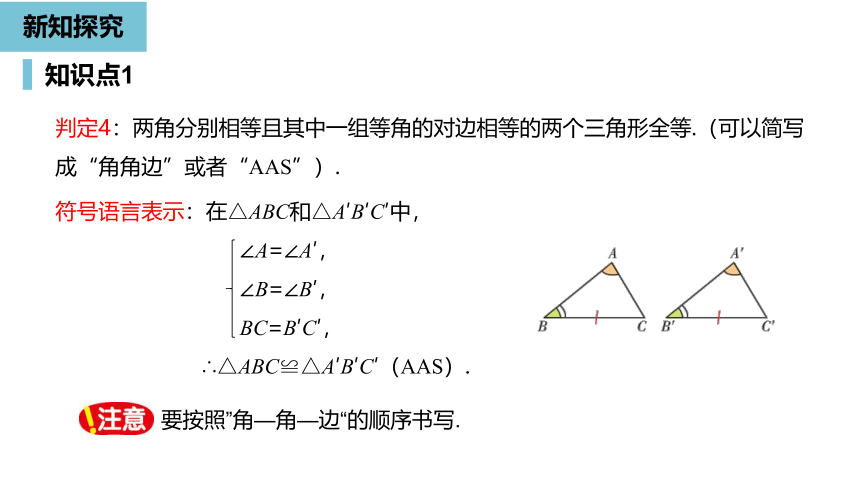
判定4:两角分别相等且其中一组等角的对边相等的两个三角形全等.(可以简写成“角角边”或者“AAS”).
符号语言表示:在△ABC和△A′B′C′中,
∠A=∠A′,
∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′(AAS).
要按照”角—角—边“的顺序书写.
例题解析
新知探究
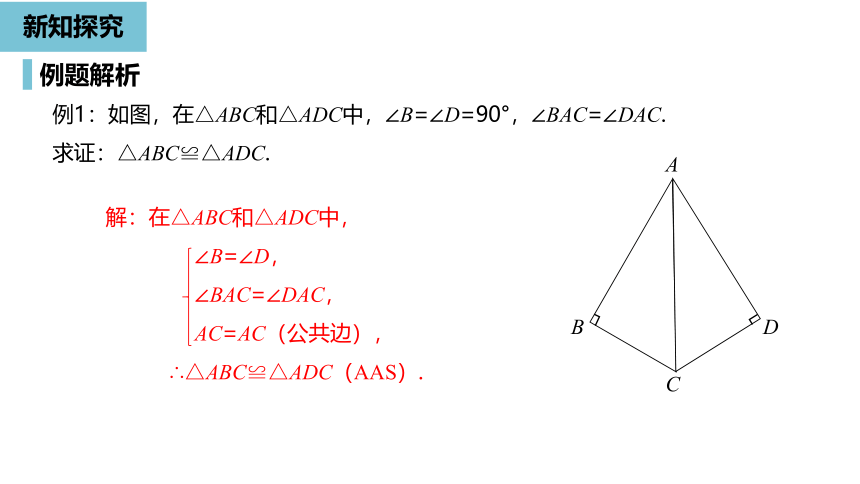
例1:如图,在△ABC和△ADC中,∠B=∠D=90°,∠BAC=∠DAC.
求证:△ABC≌△ADC.
解:在△ABC和△ADC中,
∠B=∠D,
∠BAC=∠DAC,
AC=AC(公共边),
∴△ABC≌△ADC(AAS).
┐
A
B
D
C
┐
跟踪训练
新知探究
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
分析:
利用三角形全等的性质说明AB=AC.
AB,AC分别在△AEB和△ADC中,则需要证
明△AEB≌△ADC.
题目中已有一边和两角相等,可以考虑选择
“ASA”或者“AAS”,将∠1=∠2转化成△AEB
和△ADC中相等的角即可.
C
1
B
D
A
E
2
跟踪训练
新知探究
证明:∵∠2是△AEB的外角,∴∠AEB=180°-∠2.
∵∠1是△ADC的外角,∴∠ADC=180°-∠1.
∵∠1=∠2,
∴
∠AEB=∠ADC.
在△AEB和△ADC中,
∠A=∠A
∠AEB=∠ADC,
BE=CD,
∴△AEB≌△ADC(AAS).
∴AB=AC.
1
B
D
A
E
2
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
C
知识点2
新知探究
思考:有两个角和一条边分别对应相等的两个三角形是否一定全等?
如果两个三角形中,有两个角和一条边分别相等,那么这两个三角形是全等三角形.
思考:“ASA”和“AAS”之间有什么关系?
在证明两个三角形全等过程中,“ASA”和“AAS”两个判定是可以相互转化的.
你能总结一下“ASA”和“AAS”的区别与联系吗?
知识点2
新知探究
ASA
“ASA”和'AAS”的区别与联系
“S”的意义
书写格式
联系
ASA
“S”是两角的夹边
把夹边相等写在两角相等的中间
由三角形的内角和定理可知,“ASA”和“AAS”可以互相转化
AAS
“S”是其中一角的对边
把两角相等写在一起,边相等放在最后
“ASA”和“AAS”的区别与联系
跟踪训练
新知探究
如图,点O是AB的中点,∠C=∠D,则△AOC和△BOD全等吗?请用两种方法证明.
解:△AOC和△BOD全等,理由如下:
∵点O是AB的中点,
∴OA=OB.
∵在△AOC和△BOD中,∠C=∠D,∠AOC=∠BOD,
∴∠A=∠B(三角形内角和定理).
在△AOC和△BOD中,
∠A=∠B,
OA=OB,
∠AOC=∠BOD,
∴△AOC≌△BOD(ASA).
B
A
O
D
C
跟踪训练
新知探究
解:△AOC和△BOD全等,理由如下:
∵点O是AB的中点,
∴OA=OB.
∵在△AOC和△BOD中,∠C=∠D,
∠AOC=∠BOD,
OA=OB,
∴△AOC≌△BOD(AAS).
如图,点O是AB的中点,∠C=∠D,则△AOC和△BOD全等吗?请用两种方法证明.
B
A
O
D
C
随堂练习
1
已知,如图,点E是AC上一点,AB=CE,AB//CD,∠ACB=∠D.求证:BC=ED.
证明:∵AB//CD,
∴∠A=∠ECD.
在△ACB和△CDE中,
∠ACB=∠D,
∠A=∠ECD,
AB=CE,
∴△ACB≌△CDE(AAS).
∴BC=ED.
A
B
E
C
D
随堂练习
2
如图,已知点B,E,C,F在同一直线上,AB=DE,∠A=∠D,AC//DF.
求证:(1)△ABC≌△DEF.(2)BE=CF.
证明:(1)∵AC//DF,
∴∠ACB=∠F.
在△ABC和△DEF中,
∠ACB=∠F,
∠A=∠D,
AB=DE,
∴△ABC≌△DEF(AAS).
A
C
D
F
B
E
随堂练习
2
证明:(2)∵△ABC≌△DEF,
∴BC=EF.
∴BC-EC=EF-EC,
即BE=CF.
等边加(减)等边,其和(差)还是等边,等角加(减)等角,其和(差)还是等角.
A
C
D
F
B
E
如图,已知点B,E,C,F在同一直线上,AB=DE,∠A=∠D,AC//DF.
求证:(1)△ABC≌△DEF.(2)BE=CF.
随堂练习
3
如图,已知AD=BC,AC=BD.
(1)求证:△ADB≌△BCA.
(2)OA与OB相等吗?若相等,请说明理由.
证明:(1)
∵在△ADB和△BCA中,
AD=BC,
AB=BA(公共边),
BD=
AC,
∴△ADB≌△BCA(SSS).
随堂练习
3
证明:(2)
OA与OB相等,理由如下:
由(1)得:∠D=∠C.
∵在△DOA和△COB中,
∠D=∠C,
∠DOA=∠COB,
AD=BC,
∴△DOA≌△COB(AAS),OA=OB.
如图,已知AD=BC,AC=BD.
(1)求证:△ADB≌△BCA.
(2)OA与OB相等吗?若相等,请说明理由.
课堂小结
三角形全等的判定
AAS
对比
探究
应用
两角和其中一组角的对边分别相等的两个三角形全等
对比“ASA”和“AAS”的区别和联系
利用“AAS”解决实际问题
拓展提升
1
如图,AB⊥CD,且AB=CD.E,F是AD上的两点,CE⊥AD,BF⊥AD.
若CE=a,
BF=b,EF=c,则AD的长为(
)
A.a+c
B.b+c
C.a-b+c
D.a+b-c
分析:由已知条件可证明△CED和△AFB全等.
将已知的CE、BF通过全等三角形对应边相等
转化成与AD相关的线段求解.
1、利用垂直关系得到相等的角.
2、利用转化的思想将已知条件转化为求解结果.
拓展提升
1
解:设AB,CD相交于点M.
∵CE⊥AD,AB⊥CD,
∴∠AMD=∠CED=90°.
∵∠A+∠D=90°,∠C+∠D=90°,
∴∠A=∠C.
∵BF⊥AD,
∴∠AFB=90°.
∵在△ABF和△CDE中,
∠AFB=∠CED,
∠A=∠C,
AB=CD,
∴△ABF≌△CDE(AAS).
∴AF=CE=a,BF=DE=b.
∵EF=c,
∴DF=DE-EF=b-c,则AD=AF+DF=a+b-c.
拓展提升
2
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
解:(1)
添加AE=AF,证明如下:
∵AD是∠BAC的平分线,
∴∠EAD=∠FAD.
∵在△AED和△AFD中,AE=AF,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(SAS).
已有一边和一角分别相等,可以构造一边相等选择“SAS”.
拓展提升
2
解:(2)
添加∠EDA=∠FDA
,证明如下:
∵AD是∠BAC的平分线,
∴∠EAD=∠FAD.
∵在△AED和△AFD中,∠EDA=∠FDA,
AD=AD,
∠EAD=∠FAD,
∴△AED≌△AFD(ASA).
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
已有一边和一角分别相等,可以构造一角相等选择“ASA”.
拓展提升
2
解:(3)
添加∠DEA=∠DFA,证明如下:
∵AD是∠BAC的平分线,
∴∠EAD=∠FAD.
∵在△AED和△AFD中,∠DEA=∠DFA,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(AAS).
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
已有一边和一角分别相等,可以构造一边相等选择“AAS”.
12.2.4 三角形全等的判定
全等三角形的判定
人教版-数学-八年级上册
知识回顾
1、什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
2、三边分别相等的两个三角形全等(可以简写成“边边边”或者“SSS”).
符号语言表示:在△ABC和△A'B'C'中,
AB=A'B',
AC=A'C',
BC=B'C',
∴△ABC≌△A'B'C'.
3、两边和它们的夹角分别相等的两个三角形全等(可以简写成“边角边”或者“SAS”).
符号语言表示:在△ABC和△A′B′C′中,
AB=A′B′,
∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′(SAS).
知识回顾
4、两角和它们的夹边分别相等的两个三角形全等(可以简写成“角边角”或者“ASA”).
符号语言表示:在△ABC和△A′B′C′中,
∠B=∠B′,
BC=B′C′,
∠C=∠C′,
∴△ABC≌△A′B′C′(ASA).
知识回顾
学习目标
1、理解并掌握三角形全等判定“角角边”条件的内容.
2、熟练利用“角角边”条件证明两个三角形全等.
3、通过探究判定三角形全等条件的过程,提高分析和解决问题的能力.
课堂导入
两角分别相等且其中一组等角的对边相等,这样的两个三角形全等吗?
在△ABC和△A'B'C'中,使得AB=A'B',∠C=∠C',∠B=∠B'.此时的△ABC和△A'B'C'全等吗?
请选用已经学过的全等三角形的判定来证明△ABC和△A'B'C'全等.
A
B
B'
A'
C
C'
新知探究
已知,在△ABC和△A′B′C′中,AB=A′B′,∠C=∠C′,∠B=∠B′.
证明△ABC≌△A′B′C′.
证明:∵∠C=∠C′,∠B=∠B′,
∠A=180°-∠B-∠C,
∠A′=180°-∠B′-∠C′,
∴∠A=∠A′.
∠A=∠A′,
在△ABC和△A′B′C′中,
AB=A′B′,
∠B=∠B′,
∴△ABC≌△A′B′C′(ASA).
A
B
B'
A'
C
C'
知识点1
新知探究
判定4:两角分别相等且其中一组等角的对边相等的两个三角形全等.(可以简写成“角角边”或者“AAS”).
符号语言表示:在△ABC和△A′B′C′中,
∠A=∠A′,
∠B=∠B′,
BC=B′C′,
∴△ABC≌△A′B′C′(AAS).
要按照”角—角—边“的顺序书写.
例题解析
新知探究
例1:如图,在△ABC和△ADC中,∠B=∠D=90°,∠BAC=∠DAC.
求证:△ABC≌△ADC.
解:在△ABC和△ADC中,
∠B=∠D,
∠BAC=∠DAC,
AC=AC(公共边),
∴△ABC≌△ADC(AAS).
┐
A
B
D
C
┐
跟踪训练
新知探究
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
分析:
利用三角形全等的性质说明AB=AC.
AB,AC分别在△AEB和△ADC中,则需要证
明△AEB≌△ADC.
题目中已有一边和两角相等,可以考虑选择
“ASA”或者“AAS”,将∠1=∠2转化成△AEB
和△ADC中相等的角即可.
C
1
B
D
A
E
2
跟踪训练
新知探究
证明:∵∠2是△AEB的外角,∴∠AEB=180°-∠2.
∵∠1是△ADC的外角,∴∠ADC=180°-∠1.
∵∠1=∠2,
∴
∠AEB=∠ADC.
在△AEB和△ADC中,
∠A=∠A
∠AEB=∠ADC,
BE=CD,
∴△AEB≌△ADC(AAS).
∴AB=AC.
1
B
D
A
E
2
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
C
知识点2
新知探究
思考:有两个角和一条边分别对应相等的两个三角形是否一定全等?
如果两个三角形中,有两个角和一条边分别相等,那么这两个三角形是全等三角形.
思考:“ASA”和“AAS”之间有什么关系?
在证明两个三角形全等过程中,“ASA”和“AAS”两个判定是可以相互转化的.
你能总结一下“ASA”和“AAS”的区别与联系吗?
知识点2
新知探究
ASA
“ASA”和'AAS”的区别与联系
“S”的意义
书写格式
联系
ASA
“S”是两角的夹边
把夹边相等写在两角相等的中间
由三角形的内角和定理可知,“ASA”和“AAS”可以互相转化
AAS
“S”是其中一角的对边
把两角相等写在一起,边相等放在最后
“ASA”和“AAS”的区别与联系
跟踪训练
新知探究
如图,点O是AB的中点,∠C=∠D,则△AOC和△BOD全等吗?请用两种方法证明.
解:△AOC和△BOD全等,理由如下:
∵点O是AB的中点,
∴OA=OB.
∵在△AOC和△BOD中,∠C=∠D,∠AOC=∠BOD,
∴∠A=∠B(三角形内角和定理).
在△AOC和△BOD中,
∠A=∠B,
OA=OB,
∠AOC=∠BOD,
∴△AOC≌△BOD(ASA).
B
A
O
D
C
跟踪训练
新知探究
解:△AOC和△BOD全等,理由如下:
∵点O是AB的中点,
∴OA=OB.
∵在△AOC和△BOD中,∠C=∠D,
∠AOC=∠BOD,
OA=OB,
∴△AOC≌△BOD(AAS).
如图,点O是AB的中点,∠C=∠D,则△AOC和△BOD全等吗?请用两种方法证明.
B
A
O
D
C
随堂练习
1
已知,如图,点E是AC上一点,AB=CE,AB//CD,∠ACB=∠D.求证:BC=ED.
证明:∵AB//CD,
∴∠A=∠ECD.
在△ACB和△CDE中,
∠ACB=∠D,
∠A=∠ECD,
AB=CE,
∴△ACB≌△CDE(AAS).
∴BC=ED.
A
B
E
C
D
随堂练习
2
如图,已知点B,E,C,F在同一直线上,AB=DE,∠A=∠D,AC//DF.
求证:(1)△ABC≌△DEF.(2)BE=CF.
证明:(1)∵AC//DF,
∴∠ACB=∠F.
在△ABC和△DEF中,
∠ACB=∠F,
∠A=∠D,
AB=DE,
∴△ABC≌△DEF(AAS).
A
C
D
F
B
E
随堂练习
2
证明:(2)∵△ABC≌△DEF,
∴BC=EF.
∴BC-EC=EF-EC,
即BE=CF.
等边加(减)等边,其和(差)还是等边,等角加(减)等角,其和(差)还是等角.
A
C
D
F
B
E
如图,已知点B,E,C,F在同一直线上,AB=DE,∠A=∠D,AC//DF.
求证:(1)△ABC≌△DEF.(2)BE=CF.
随堂练习
3
如图,已知AD=BC,AC=BD.
(1)求证:△ADB≌△BCA.
(2)OA与OB相等吗?若相等,请说明理由.
证明:(1)
∵在△ADB和△BCA中,
AD=BC,
AB=BA(公共边),
BD=
AC,
∴△ADB≌△BCA(SSS).
随堂练习
3
证明:(2)
OA与OB相等,理由如下:
由(1)得:∠D=∠C.
∵在△DOA和△COB中,
∠D=∠C,
∠DOA=∠COB,
AD=BC,
∴△DOA≌△COB(AAS),OA=OB.
如图,已知AD=BC,AC=BD.
(1)求证:△ADB≌△BCA.
(2)OA与OB相等吗?若相等,请说明理由.
课堂小结
三角形全等的判定
AAS
对比
探究
应用
两角和其中一组角的对边分别相等的两个三角形全等
对比“ASA”和“AAS”的区别和联系
利用“AAS”解决实际问题
拓展提升
1
如图,AB⊥CD,且AB=CD.E,F是AD上的两点,CE⊥AD,BF⊥AD.
若CE=a,
BF=b,EF=c,则AD的长为(
)
A.a+c
B.b+c
C.a-b+c
D.a+b-c
分析:由已知条件可证明△CED和△AFB全等.
将已知的CE、BF通过全等三角形对应边相等
转化成与AD相关的线段求解.
1、利用垂直关系得到相等的角.
2、利用转化的思想将已知条件转化为求解结果.
拓展提升
1
解:设AB,CD相交于点M.
∵CE⊥AD,AB⊥CD,
∴∠AMD=∠CED=90°.
∵∠A+∠D=90°,∠C+∠D=90°,
∴∠A=∠C.
∵BF⊥AD,
∴∠AFB=90°.
∵在△ABF和△CDE中,
∠AFB=∠CED,
∠A=∠C,
AB=CD,
∴△ABF≌△CDE(AAS).
∴AF=CE=a,BF=DE=b.
∵EF=c,
∴DF=DE-EF=b-c,则AD=AF+DF=a+b-c.
拓展提升
2
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
解:(1)
添加AE=AF,证明如下:
∵AD是∠BAC的平分线,
∴∠EAD=∠FAD.
∵在△AED和△AFD中,AE=AF,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(SAS).
已有一边和一角分别相等,可以构造一边相等选择“SAS”.
拓展提升
2
解:(2)
添加∠EDA=∠FDA
,证明如下:
∵AD是∠BAC的平分线,
∴∠EAD=∠FAD.
∵在△AED和△AFD中,∠EDA=∠FDA,
AD=AD,
∠EAD=∠FAD,
∴△AED≌△AFD(ASA).
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
已有一边和一角分别相等,可以构造一角相等选择“ASA”.
拓展提升
2
解:(3)
添加∠DEA=∠DFA,证明如下:
∵AD是∠BAC的平分线,
∴∠EAD=∠FAD.
∵在△AED和△AFD中,∠DEA=∠DFA,
∠EAD=∠FAD,
AD=AD,
∴△AED≌△AFD(AAS).
如图,已知AD是∠BAC的平分线,在不添加任何辅助线的前提下,要△AED≌△AFD,可添加一个什么条件?并给予证明.
已有一边和一角分别相等,可以构造一边相等选择“AAS”.
