人教版八年级数学上册12.3角平分线的性质课时2课件(24张PPT)
文档属性
| 名称 | 人教版八年级数学上册12.3角平分线的性质课时2课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 199.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 07:50:18 | ||
图片预览





文档简介
(共24张PPT)
12.3.2 角平分线的判定
角平分线的性质
知识回顾
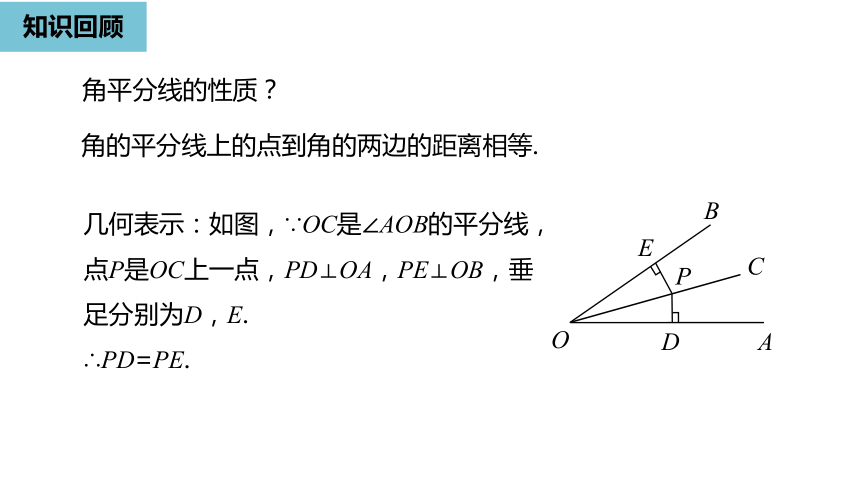
角平分线的性质?
角的平分线上的点到角的两边的距离相等.
几何表示:如图,∵OC是∠AOB的平分线,点P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.
∴PD=PE.
O
A
B
C
P
D
E
┐
┐
学习目标
1、探究并证明角的平分线的判定.
2、会用角的平分线的判定解决实际问题.
3、熟练掌握角的平分线的性质和角的平分线的判定的综合运用.
课堂导入
思考:如图,要在S区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路与铁路的交叉处500m.这个集贸市场应建于何处?
作出公路和铁路相交的角的平分线,按照比例尺的比例在该平分线上选取离交叉口处500m的位置即可建集贸市场.
到角的两边的距离相等的点是否在角的平分线上?
知识点1
新知探究
角的平分线的判定定理:角的内部到角的两边的距离相等的点在角的平分线上.
几何表示:如图,∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,
∴点P在∠AOB的平分线OC上.
(1)使用该判定定理的前提是这个点必须在角的内部;
(2)角的平分线的判定定理是证明两角相等的重要办法.
O
A
B
C
P
D
E
┐
┐
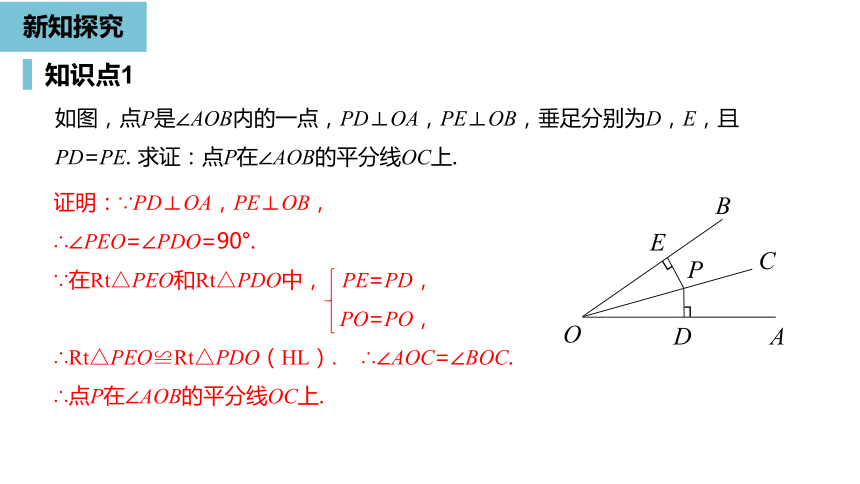
证明:∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°.
∵在Rt△PEO和Rt△PDO中,
PE=PD,
PO=PO,
∴Rt△PEO≌Rt△PDO(HL).
∴∠AOC=∠BOC.
∴点P在∠AOB的平分线OC上.
知识点1
新知探究
如图,点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE.
求证:点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
┐
角的平分线的性质定理与判定定理的关系.
知识点2
新知探究
点在角的平分线上
(角的内部)点到角
的两边的距离相等
性质定理
判定定理
正确理解两个定理的条件和结论,性质定理和判定定理的条件和结论是相反的,性质定理是证明两条线段相等的依据,判定定理是证明两个角相等的依据.
知识点3
新知探究
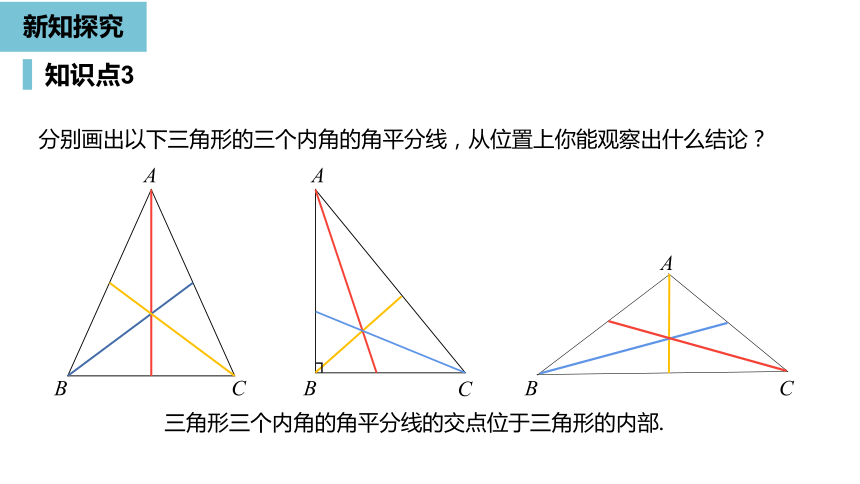
分别画出以下三角形的三个内角的角平分线,从位置上你能观察出什么结论?
┐
三角形三个内角的角平分线的交点位于三角形的内部.
A
A
B
B
C
C
A
B
C
知识点3
新知探究
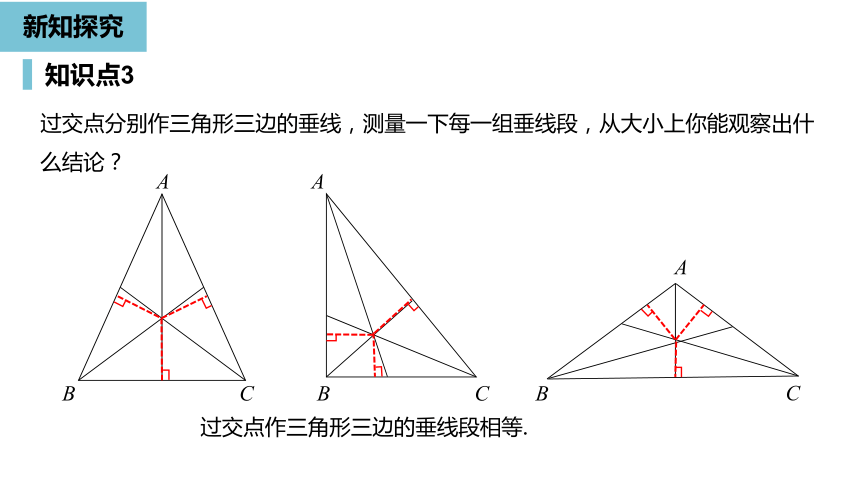
过交点分别作三角形三边的垂线,测量一下每一组垂线段,从大小上你能观察出什么结论?
过交点作三角形三边的垂线段相等.
┐
┐
┐
┐
┐
┐
┐
┐
┐
A
B
C
A
B
B
C
A
C
知识点3
新知探究
如图,△ABC的角平分线AD、BE、CF相交于点P.求证:点P到△ABC三边AB,BC,CA的距离相等.
B
C
P
D
E
F
M
N
O
证明:过点P作PM⊥BC,PN⊥AC,PO⊥AB,
垂足分别为点M,N,O.
┐
┐
∵AD为△ABC的角平分线,
∴PN=PO.
∵BE为△ABC的角平分线,
∴PM=PO.
∵CF为△ABC的角平分线,
∴PM=PN.
∴PM=PN=PO,即点P到△ABC三边AB、BC、CA的距离相等.
┐
A
知识点3
新知探究
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等,反之,三角形内部到三边距离相等的点是该三角形三条角平分线的交点.
A
B
C
P
1、判断题:
(1)如图1,若QM=QN,则OQ平分∠AOB.(
)
(2)如图2,若QM⊥OA于点M,QN⊥OB于点N,则OQ平分∠AOB.(
)
跟踪训练
新知探究
×
×
O
B
A
M
图2
N
O
B
A
Q
M
图1
N
┐
Q
┐
随堂练习
1
如图,P是△ABC外部一点,PD⊥AB,交AB的延长线于点D,PE⊥AC,交AC的延长线于点E,PF⊥BC于点F,且PD=PE=PF.关于点P有下列三种说法:①点P在∠DBC的平分线上;②点P在∠BCE的平分线上;③点P在∠BAC的平分线上.其中说法正确的个数为(
)
A.0
B.1
C.2
D.3
D
C
A
E
B
D
F
P
┐
┐
随堂练习
2
分析:AD是∠BAC的平分线.
(角的平分线的判定)
DE⊥AB,DF⊥AC
,DE=DF.
(三角形全等的判定)
Rt△DEB≌Rt△DFC.
(直角三角形全等”HL“)
BE=CF,DB=DC.
如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F且DB=DC.求证:AD是∠BAC的平分线.
C
E
A
F
D
B
┐
┐
随堂练习
2
证明:∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴∠BED=∠CFD=90°.
∵在Rt△BDE和Rt△CDF中,
BE=CF,
DB=DC,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF.
∴点D在∠BAC的平分线上,即AD是∠BAC的平分线.
如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F且DB=DC.求证:AD是∠BAC的平分线.
C
E
A
F
D
B
┐
┐
随堂练习
3
分析:OF、OD、OE为点O到三边的距离,
且OF=OD=OE.
(角的平分线的判定)
OB、OC分别平分∠ABC和∠ACB.
(角的平分线的性质)
∠OBC=∠OBA,
∠OCB=∠OCA.
(三角形内角和定理)
转化为
∠BAC和∠BOC的关系.
如图,O是△ABC内一点,O到三边AB,BC,CA的距离分别为OF,OD,OE,且OF=OD=OE,若∠BAC=70°,则∠BOC=(
).
随堂练习
3
125°
证明:∵OF=OD=OE,
∴OB、OC分别平分∠ABC和∠ACB.
∵∠BAC=70°,
∴∠ABC+∠ACB=180°-∠BAC=110°.
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=55°.
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
如图,O是△ABC内一点,O到三边AB,BC,CA的距离分别为OF,OD,OE,且OF=OD=OE,若∠BAC=70°,则∠BOC=(
).
随堂练习
4
如图,在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
E
A
B
C
D
F
┌
┐
分析:
AC平分∠BAD.
(角的平分线的判定)
CF=CE.
(全等三角形的性质)
△CFB≌△CED.
(全等三角形的判定)
∠ADB+∠ABC=180°,BC=DC(转化已知条件).
随堂练习
4
证明:∵∠ADC+∠ABC=180°,∠ADC+∠EDC=180°,
∴∠ABC=∠EDC.
∵CE⊥AD,CF⊥AB,
∴∠CED=∠CFB=90°.
∵在△BCF和△DCE中,
∠CFB=∠CED,
∠FBC=∠EDC,
BC=DC,
∴△BCF≌△DCE(AAS).
∴CF=CE,即AC平分∠BAD.
如图,在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
E
A
B
C
D
F
┌
┐
课堂小结
角平分线
的判定
学会用添加辅助线的方法解题
判定
定理
应用
角的内部到角的两边的距离相等的点在角的平分线上
综合利用角的平分线的性质和判定来解决实际问题
拓展提升
1
如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.
分析:AE是∠DAB的平分线.
(角的平分线的判定)
点E到AB、AD的距离相等(BE=FE
).
(等量代换)
BE=CE,EF=CE.
(角的平分线的性质)
DE平分∠ADC,∠DFE=∠C=90°.
A
B
C
E
D
┌
┌
拓展提升
1
证明:过点E作EF⊥AD于点F,
∵∠B=∠C=90°,
∴DC⊥EC,EB⊥AB.
∵DE平分∠ADC,
∴EC=EF.
∵E是BC的中点,
∴EC=EB.
又∵EF⊥AD,EB⊥AB,
∴点E在∠BAD的平分线上,即AE是∠DAB的平分线.
如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.
A
B
C
E
D
┌
┌
F
┌
拓展提升
2
如图,∠MON=60°,点A,B为射线OM,ON上的动点(点A、B不与点O重合),在∠MON的内部,△AOB的外部有一点P,且AP=BP,∠APB=120°.
求证:点P在∠MON的平分线上.
分析:(1)过点P分别向OM、ON作垂线段,利用角的平分线的判定来证明结论;
(2)等角加(减)等角,其和(差)仍然是等角;
(3)证明两条线段相等利用三角形全等的性质.
O
A
B
P
M
N
证明:过点P分别作PC⊥OM,PB⊥ON,垂足分别为C,D,
则∠ACP=∠BDP=90°.
在四边形OCPD中,
∠CPD=360°-∠OCP-∠COD-∠ODP=120°,
∴∠APB=∠CPD.
∴∠APB-∠APD
=∠CPD-∠APD,即∠APC=∠BPD.
在△APC和△BPD中,
∠APC=∠BPD,
∠ACP=∠BDP,
AP=BP,
∴△APC≌△BPD(AAS).
∴PC=PD,即点P在∠MON的平分线上.
拓展提升
2
O
A
B
P
M
N
D
C
┌
┌
12.3.2 角平分线的判定
角平分线的性质
知识回顾
角平分线的性质?
角的平分线上的点到角的两边的距离相等.
几何表示:如图,∵OC是∠AOB的平分线,点P是OC上一点,PD⊥OA,PE⊥OB,垂足分别为D,E.
∴PD=PE.
O
A
B
C
P
D
E
┐
┐
学习目标
1、探究并证明角的平分线的判定.
2、会用角的平分线的判定解决实际问题.
3、熟练掌握角的平分线的性质和角的平分线的判定的综合运用.
课堂导入
思考:如图,要在S区建一个集贸市场,使它到公路、铁路的距离相等,并且离公路与铁路的交叉处500m.这个集贸市场应建于何处?
作出公路和铁路相交的角的平分线,按照比例尺的比例在该平分线上选取离交叉口处500m的位置即可建集贸市场.
到角的两边的距离相等的点是否在角的平分线上?
知识点1
新知探究
角的平分线的判定定理:角的内部到角的两边的距离相等的点在角的平分线上.
几何表示:如图,∵点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE,
∴点P在∠AOB的平分线OC上.
(1)使用该判定定理的前提是这个点必须在角的内部;
(2)角的平分线的判定定理是证明两角相等的重要办法.
O
A
B
C
P
D
E
┐
┐
证明:∵PD⊥OA,PE⊥OB,
∴∠PEO=∠PDO=90°.
∵在Rt△PEO和Rt△PDO中,
PE=PD,
PO=PO,
∴Rt△PEO≌Rt△PDO(HL).
∴∠AOC=∠BOC.
∴点P在∠AOB的平分线OC上.
知识点1
新知探究
如图,点P是∠AOB内的一点,PD⊥OA,PE⊥OB,垂足分别为D,E,且PD=PE.
求证:点P在∠AOB的平分线OC上.
O
A
B
C
P
D
E
┐
┐
角的平分线的性质定理与判定定理的关系.
知识点2
新知探究
点在角的平分线上
(角的内部)点到角
的两边的距离相等
性质定理
判定定理
正确理解两个定理的条件和结论,性质定理和判定定理的条件和结论是相反的,性质定理是证明两条线段相等的依据,判定定理是证明两个角相等的依据.
知识点3
新知探究
分别画出以下三角形的三个内角的角平分线,从位置上你能观察出什么结论?
┐
三角形三个内角的角平分线的交点位于三角形的内部.
A
A
B
B
C
C
A
B
C
知识点3
新知探究
过交点分别作三角形三边的垂线,测量一下每一组垂线段,从大小上你能观察出什么结论?
过交点作三角形三边的垂线段相等.
┐
┐
┐
┐
┐
┐
┐
┐
┐
A
B
C
A
B
B
C
A
C
知识点3
新知探究
如图,△ABC的角平分线AD、BE、CF相交于点P.求证:点P到△ABC三边AB,BC,CA的距离相等.
B
C
P
D
E
F
M
N
O
证明:过点P作PM⊥BC,PN⊥AC,PO⊥AB,
垂足分别为点M,N,O.
┐
┐
∵AD为△ABC的角平分线,
∴PN=PO.
∵BE为△ABC的角平分线,
∴PM=PO.
∵CF为△ABC的角平分线,
∴PM=PN.
∴PM=PN=PO,即点P到△ABC三边AB、BC、CA的距离相等.
┐
A
知识点3
新知探究
三角形的三条角平分线相交于三角形内一点,且该点到三角形三边的距离相等,反之,三角形内部到三边距离相等的点是该三角形三条角平分线的交点.
A
B
C
P
1、判断题:
(1)如图1,若QM=QN,则OQ平分∠AOB.(
)
(2)如图2,若QM⊥OA于点M,QN⊥OB于点N,则OQ平分∠AOB.(
)
跟踪训练
新知探究
×
×
O
B
A
M
图2
N
O
B
A
Q
M
图1
N
┐
Q
┐
随堂练习
1
如图,P是△ABC外部一点,PD⊥AB,交AB的延长线于点D,PE⊥AC,交AC的延长线于点E,PF⊥BC于点F,且PD=PE=PF.关于点P有下列三种说法:①点P在∠DBC的平分线上;②点P在∠BCE的平分线上;③点P在∠BAC的平分线上.其中说法正确的个数为(
)
A.0
B.1
C.2
D.3
D
C
A
E
B
D
F
P
┐
┐
随堂练习
2
分析:AD是∠BAC的平分线.
(角的平分线的判定)
DE⊥AB,DF⊥AC
,DE=DF.
(三角形全等的判定)
Rt△DEB≌Rt△DFC.
(直角三角形全等”HL“)
BE=CF,DB=DC.
如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F且DB=DC.求证:AD是∠BAC的平分线.
C
E
A
F
D
B
┐
┐
随堂练习
2
证明:∵DE⊥AB的延长线于点E,DF⊥AC于点F,
∴∠BED=∠CFD=90°.
∵在Rt△BDE和Rt△CDF中,
BE=CF,
DB=DC,
∴Rt△BDE≌Rt△CDF(HL).
∴DE=DF.
∴点D在∠BAC的平分线上,即AD是∠BAC的平分线.
如图,BE=CF,DE⊥AB的延长线于点E,DF⊥AC于点F且DB=DC.求证:AD是∠BAC的平分线.
C
E
A
F
D
B
┐
┐
随堂练习
3
分析:OF、OD、OE为点O到三边的距离,
且OF=OD=OE.
(角的平分线的判定)
OB、OC分别平分∠ABC和∠ACB.
(角的平分线的性质)
∠OBC=∠OBA,
∠OCB=∠OCA.
(三角形内角和定理)
转化为
∠BAC和∠BOC的关系.
如图,O是△ABC内一点,O到三边AB,BC,CA的距离分别为OF,OD,OE,且OF=OD=OE,若∠BAC=70°,则∠BOC=(
).
随堂练习
3
125°
证明:∵OF=OD=OE,
∴OB、OC分别平分∠ABC和∠ACB.
∵∠BAC=70°,
∴∠ABC+∠ACB=180°-∠BAC=110°.
∴∠OBC+∠OCB=
(∠ABC+∠ACB)=55°.
∴∠BOC=180°-(∠OBC+∠OCB)=125°.
如图,O是△ABC内一点,O到三边AB,BC,CA的距离分别为OF,OD,OE,且OF=OD=OE,若∠BAC=70°,则∠BOC=(
).
随堂练习
4
如图,在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
E
A
B
C
D
F
┌
┐
分析:
AC平分∠BAD.
(角的平分线的判定)
CF=CE.
(全等三角形的性质)
△CFB≌△CED.
(全等三角形的判定)
∠ADB+∠ABC=180°,BC=DC(转化已知条件).
随堂练习
4
证明:∵∠ADC+∠ABC=180°,∠ADC+∠EDC=180°,
∴∠ABC=∠EDC.
∵CE⊥AD,CF⊥AB,
∴∠CED=∠CFB=90°.
∵在△BCF和△DCE中,
∠CFB=∠CED,
∠FBC=∠EDC,
BC=DC,
∴△BCF≌△DCE(AAS).
∴CF=CE,即AC平分∠BAD.
如图,在四边形ABCD中,∠ADC+∠ABC=180°,BC=DC,CE⊥AD,交AD的延长线于点E,CF⊥AB于点F.求证:AC平分∠BAD.
E
A
B
C
D
F
┌
┐
课堂小结
角平分线
的判定
学会用添加辅助线的方法解题
判定
定理
应用
角的内部到角的两边的距离相等的点在角的平分线上
综合利用角的平分线的性质和判定来解决实际问题
拓展提升
1
如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.
分析:AE是∠DAB的平分线.
(角的平分线的判定)
点E到AB、AD的距离相等(BE=FE
).
(等量代换)
BE=CE,EF=CE.
(角的平分线的性质)
DE平分∠ADC,∠DFE=∠C=90°.
A
B
C
E
D
┌
┌
拓展提升
1
证明:过点E作EF⊥AD于点F,
∵∠B=∠C=90°,
∴DC⊥EC,EB⊥AB.
∵DE平分∠ADC,
∴EC=EF.
∵E是BC的中点,
∴EC=EB.
又∵EF⊥AD,EB⊥AB,
∴点E在∠BAD的平分线上,即AE是∠DAB的平分线.
如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.求证:AE是∠DAB的平分线.
A
B
C
E
D
┌
┌
F
┌
拓展提升
2
如图,∠MON=60°,点A,B为射线OM,ON上的动点(点A、B不与点O重合),在∠MON的内部,△AOB的外部有一点P,且AP=BP,∠APB=120°.
求证:点P在∠MON的平分线上.
分析:(1)过点P分别向OM、ON作垂线段,利用角的平分线的判定来证明结论;
(2)等角加(减)等角,其和(差)仍然是等角;
(3)证明两条线段相等利用三角形全等的性质.
O
A
B
P
M
N
证明:过点P分别作PC⊥OM,PB⊥ON,垂足分别为C,D,
则∠ACP=∠BDP=90°.
在四边形OCPD中,
∠CPD=360°-∠OCP-∠COD-∠ODP=120°,
∴∠APB=∠CPD.
∴∠APB-∠APD
=∠CPD-∠APD,即∠APC=∠BPD.
在△APC和△BPD中,
∠APC=∠BPD,
∠ACP=∠BDP,
AP=BP,
∴△APC≌△BPD(AAS).
∴PC=PD,即点P在∠MON的平分线上.
拓展提升
2
O
A
B
P
M
N
D
C
┌
┌
