人教版八年级数学上册13.1轴对称课时1课件(23张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.1轴对称课时1课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
13.1.1 轴对称
轴对称
人教版-数学-八年级上册
知识回顾
1、角平分线的概念
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
如图,OC是∠AOB的平分线,
∠AOC=∠BOC=
∠AOB.
A
B
C
O
学习目标
1、通过观察实例,了解轴对称图形和两个图形成轴对称
的概念.
2、掌握轴对称图形的性质和成轴对称的两个图形的性质
并能解决实际问题.
课堂导入
仔细观察,你能从这些图片中得到什么规律?
以上图形沿着一条直线翻折后,直线两旁的两个部
分能够完全重合.
知识点1
新知探究
概念:
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
此时,也说这个图形关于这条直线(成轴)对称.
(1)轴对称图形是对一个图形来讲的,它是一个图形自身的对称特征,它被对称轴分成的两部分能够互相重合.
(2)一个轴对称图形的对称轴可以有一条,也可以有多条.
轴对称图形
新知探究
根据以上的定义,你能举出生活中见过的一些轴对称图形的例子吗?
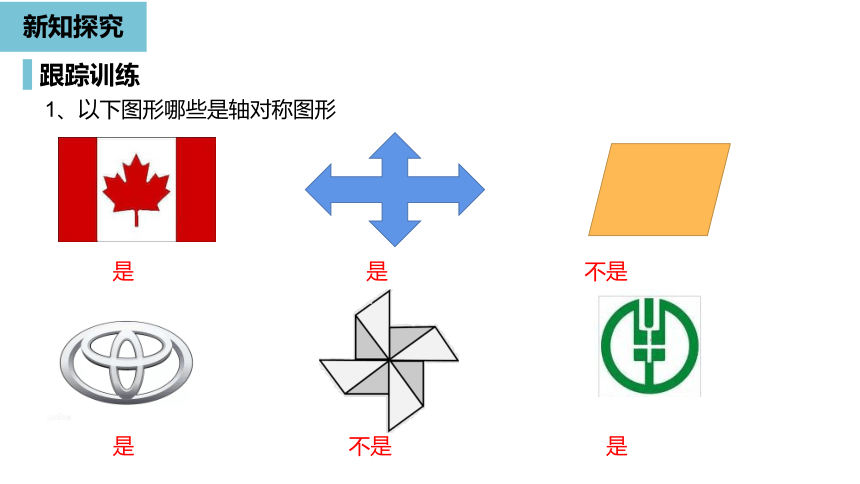
1、以下图形哪些是轴对称图形
新知探究
跟踪训练
是
是
不是
是
不是
是
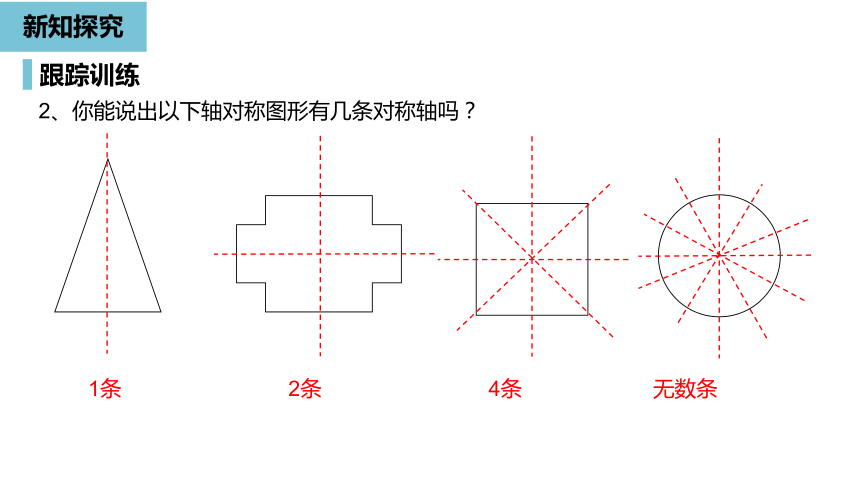
2、你能说出以下轴对称图形有几条对称轴吗?
新知探究
跟踪训练
1条
2条
4条
无数条
新知探究
1、一个轴对称图形的对称轴可以有一条,也可以有多条,甚至有无数条.
2、轴对称图形的对称轴通常画成直线、虚线.
思考:以下常见的轴对称图形分别有几条对称轴,对称轴分别是哪些直线?
角、等腰三角形、等边三角形、等腰梯形、长方形、正方形、正五边形、正六边形、圆.
新知探究
图形名称
图形
对称轴
对称轴的条数
角
角平分线所在的直线
1
等腰三角形
底边上的高(底边上的中线、顶角平分线)所在的直线
1
等边三角形
各边上的高(内角平分线、各边上的中线)所在的直线
3
等腰梯形
上、下底的中点所在的直线
1
长方形
对边中点所在的直线
2
新知探究
图形名称
图形
对称轴
对称轴的条数
正方形
对边中点所在的直线
两条对角线所在的直线
4
正五边形
过一边中点且与该边垂直的直线
5
正六边形
相对的顶点所在的直线
对边中点所在的直线
6
圆
过圆心的每一条直线
无数
新知探究
仔细观察,下列每对图片有什么共同特点?
图中的每一对图形沿着虚线折叠,左边的图形能够
和右边的图形重合.
知识点2
新知探究
概念:把一个图形沿着某一条直线折叠,如果它能够与另外一个图形重合,那么就说这两个图形关于这条直线(成轴)对称.这条直线叫做对称轴,折叠后能够重合的点是对应点,叫做对称点.
理解轴对称定义的三点:1、有两个图形;2、存在一条直线;3、使得一个图形沿着这条直线折叠后与另外一个图形重合.
轴对称
1、分别观察以下每组图形,判断它们是否关于某条直线成轴对称?
新知探究
跟踪训练
不是
不是
是
是
不是
是
E
E
E
E
E
E
E
E
E
E
E
E
新知探究
仔细观察,下列两个图形有什么区别?
轴对称图形
两个图形成轴对称
轴对称图形和轴对称的区别和联系
新知探究
名
称
关
系
轴对称图形
轴对称
区别
对象不同
意义不同
对称点和位置不同
对称轴的数量不同
联系
一个图形
两个图形
一个形状特殊的图形
两个图形之间的特殊关系
对称点在这个图形上
对称点分别在这两个图形上
一条或者多条或者无数条
只有一条
1、都能沿着某条直线折叠后相互重合;
2、把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.把一个轴对称图形沿着对称轴分成两个图形,这两个图形关于这条轴对称.
随堂练习
1
如下字体的四个汉字,是轴对称图形的是(
)
A.书
B.香
C.宜
D.昌
D
选项D中的汉字沿着竖直的一条直线折叠,直线两旁的部分能够互相重合.注意B选项和C选项中均不能满足轴对称图形的定义,要看清楚香的“禾”和宜的
“宀”.
随堂练习
2
如图所示的每个图形是轴对称图形吗?如果是,指出它的对称轴.
是,1条
不是
是,2条
是,4条
新知探究
随堂练习
3
如图所示的每幅图形中的两个图案是轴对称吗?如果是,指出它的对称轴和对称点.
G
G
A
B
C
D
E
A1
B1
C1
D1
E1
是
A和A1,B和B1,
C和C1,D和D1,
E和E1.
是
A和A1,B和B1,
C和C1,D和D1.
不是
A
A1
B
B1
C
C1
D
D1
课堂小结
轴对称图形
定义
区别和联系
应用
轴对称图形和两个图形成轴对称
利用轴对称图形和两个图形成轴对称的定义进行判断
1、轴对称图形
2、两个图形成轴对称
拓展提升
1
下列图形,不是轴对称图形的是(
)
A
B
C
D
C
拓展提升
2
判断下列说法的对错:
1、轴对称图形必有对称轴.(
)
2、轴对称图形至少有一条对称轴.(
)
3、关于某直线成轴对称的两个图形必能互相重合.(
)
4、两个完全互相重合的图形必是轴对称.(
)
5、两个图形成轴对称,则这两个图形是全等形.(
)
√
√
√
×
√
拓展提升
3
完成下列填空:
1、成轴对称的两个图形的对应角(
),对应边(
).
2、在“线段、钝角、长方形、等边三角形”这四个图形中,是轴对称图形的有(
)个,其中对称轴最多的是(
),线段的对称轴是(
).
3、成轴对称的两个图形(
)全等形;把一个轴对称图形沿着对称轴分成两个图形,这两个图形(
)全等形.(填“是”或“否”)
相等
相等
4
等边三角形
经过线段中点且垂直于线段的直线
是
是
13.1.1 轴对称
轴对称
人教版-数学-八年级上册
知识回顾
1、角平分线的概念
一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.
如图,OC是∠AOB的平分线,
∠AOC=∠BOC=
∠AOB.
A
B
C
O
学习目标
1、通过观察实例,了解轴对称图形和两个图形成轴对称
的概念.
2、掌握轴对称图形的性质和成轴对称的两个图形的性质
并能解决实际问题.
课堂导入
仔细观察,你能从这些图片中得到什么规律?
以上图形沿着一条直线翻折后,直线两旁的两个部
分能够完全重合.
知识点1
新知探究
概念:
如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
此时,也说这个图形关于这条直线(成轴)对称.
(1)轴对称图形是对一个图形来讲的,它是一个图形自身的对称特征,它被对称轴分成的两部分能够互相重合.
(2)一个轴对称图形的对称轴可以有一条,也可以有多条.
轴对称图形
新知探究
根据以上的定义,你能举出生活中见过的一些轴对称图形的例子吗?
1、以下图形哪些是轴对称图形
新知探究
跟踪训练
是
是
不是
是
不是
是
2、你能说出以下轴对称图形有几条对称轴吗?
新知探究
跟踪训练
1条
2条
4条
无数条
新知探究
1、一个轴对称图形的对称轴可以有一条,也可以有多条,甚至有无数条.
2、轴对称图形的对称轴通常画成直线、虚线.
思考:以下常见的轴对称图形分别有几条对称轴,对称轴分别是哪些直线?
角、等腰三角形、等边三角形、等腰梯形、长方形、正方形、正五边形、正六边形、圆.
新知探究
图形名称
图形
对称轴
对称轴的条数
角
角平分线所在的直线
1
等腰三角形
底边上的高(底边上的中线、顶角平分线)所在的直线
1
等边三角形
各边上的高(内角平分线、各边上的中线)所在的直线
3
等腰梯形
上、下底的中点所在的直线
1
长方形
对边中点所在的直线
2
新知探究
图形名称
图形
对称轴
对称轴的条数
正方形
对边中点所在的直线
两条对角线所在的直线
4
正五边形
过一边中点且与该边垂直的直线
5
正六边形
相对的顶点所在的直线
对边中点所在的直线
6
圆
过圆心的每一条直线
无数
新知探究
仔细观察,下列每对图片有什么共同特点?
图中的每一对图形沿着虚线折叠,左边的图形能够
和右边的图形重合.
知识点2
新知探究
概念:把一个图形沿着某一条直线折叠,如果它能够与另外一个图形重合,那么就说这两个图形关于这条直线(成轴)对称.这条直线叫做对称轴,折叠后能够重合的点是对应点,叫做对称点.
理解轴对称定义的三点:1、有两个图形;2、存在一条直线;3、使得一个图形沿着这条直线折叠后与另外一个图形重合.
轴对称
1、分别观察以下每组图形,判断它们是否关于某条直线成轴对称?
新知探究
跟踪训练
不是
不是
是
是
不是
是
E
E
E
E
E
E
E
E
E
E
E
E
新知探究
仔细观察,下列两个图形有什么区别?
轴对称图形
两个图形成轴对称
轴对称图形和轴对称的区别和联系
新知探究
名
称
关
系
轴对称图形
轴对称
区别
对象不同
意义不同
对称点和位置不同
对称轴的数量不同
联系
一个图形
两个图形
一个形状特殊的图形
两个图形之间的特殊关系
对称点在这个图形上
对称点分别在这两个图形上
一条或者多条或者无数条
只有一条
1、都能沿着某条直线折叠后相互重合;
2、把成轴对称的两个图形看成一个整体,它就是一个轴对称图形.把一个轴对称图形沿着对称轴分成两个图形,这两个图形关于这条轴对称.
随堂练习
1
如下字体的四个汉字,是轴对称图形的是(
)
A.书
B.香
C.宜
D.昌
D
选项D中的汉字沿着竖直的一条直线折叠,直线两旁的部分能够互相重合.注意B选项和C选项中均不能满足轴对称图形的定义,要看清楚香的“禾”和宜的
“宀”.
随堂练习
2
如图所示的每个图形是轴对称图形吗?如果是,指出它的对称轴.
是,1条
不是
是,2条
是,4条
新知探究
随堂练习
3
如图所示的每幅图形中的两个图案是轴对称吗?如果是,指出它的对称轴和对称点.
G
G
A
B
C
D
E
A1
B1
C1
D1
E1
是
A和A1,B和B1,
C和C1,D和D1,
E和E1.
是
A和A1,B和B1,
C和C1,D和D1.
不是
A
A1
B
B1
C
C1
D
D1
课堂小结
轴对称图形
定义
区别和联系
应用
轴对称图形和两个图形成轴对称
利用轴对称图形和两个图形成轴对称的定义进行判断
1、轴对称图形
2、两个图形成轴对称
拓展提升
1
下列图形,不是轴对称图形的是(
)
A
B
C
D
C
拓展提升
2
判断下列说法的对错:
1、轴对称图形必有对称轴.(
)
2、轴对称图形至少有一条对称轴.(
)
3、关于某直线成轴对称的两个图形必能互相重合.(
)
4、两个完全互相重合的图形必是轴对称.(
)
5、两个图形成轴对称,则这两个图形是全等形.(
)
√
√
√
×
√
拓展提升
3
完成下列填空:
1、成轴对称的两个图形的对应角(
),对应边(
).
2、在“线段、钝角、长方形、等边三角形”这四个图形中,是轴对称图形的有(
)个,其中对称轴最多的是(
),线段的对称轴是(
).
3、成轴对称的两个图形(
)全等形;把一个轴对称图形沿着对称轴分成两个图形,这两个图形(
)全等形.(填“是”或“否”)
相等
相等
4
等边三角形
经过线段中点且垂直于线段的直线
是
是
