人教版八年级数学上册13.1轴对称课时3课件(24张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.1轴对称课时3课件(24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 644.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 09:30:17 | ||
图片预览






文档简介
(共24张PPT)
13.1.3 垂直平分线
轴对称
知识回顾
1、线段是轴对称图形吗?它的对称轴是什么?
2、什么是线段的垂直平分线?
线段是轴对称图形,它的对称轴是这条线段的垂直平分线.
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
学习目标
1、理解并掌握线段垂直平分线的性质和判定的内容.
2、探究线段垂直平分线的性质和判定的过程.
3、熟练运用线段垂直平分线的性质和判定解决实际问题.
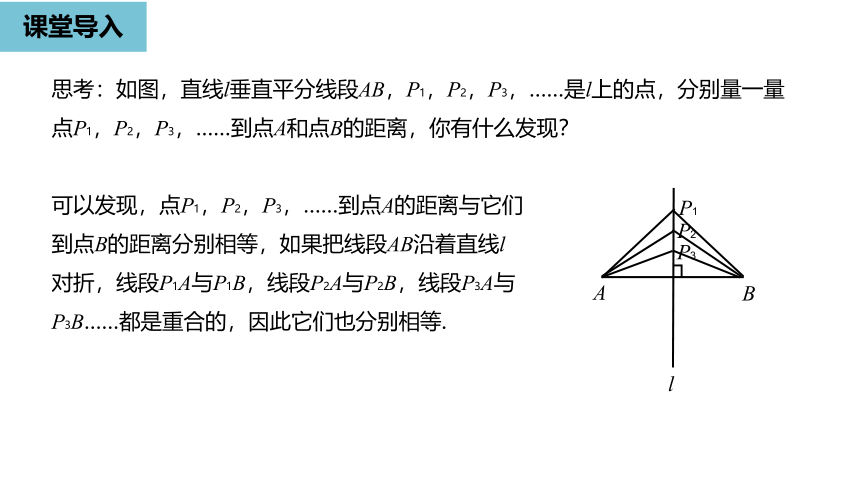
课堂导入
思考:如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,分别量一量点P1,P2,P3,……到点A和点B的距离,你有什么发现?
可以发现,点P1,P2,P3,……到点A的距离与它们到点B的距离分别相等,如果把线段AB沿着直线l对折,线段P1A与P1B,线段P2A与P2B,线段P3A与P3B……都是重合的,因此它们也分别相等.
A
B
l
┐
P1
P2
P3
课堂导入
证明:∵直线l垂直平分线段AB,
∴AO=BO,∠P1OA=∠P1OB=90°.
∵在△P1AO和△P1BO中,AO=BO,
∠P1OA=∠P1OB,
P1O=P1O,
∴△P1AO≌△P1BO(SAS).
∴P1A=P1B.
A
B
l
┐
P1
P2
P3
思考:如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,分别量一量点P1,P2,P3,……到点A和点B的距离,你有什么发现?
知识点1
新知探究
线段的垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.
符号表示:如图,直线l⊥AB,垂足为O,AO=BO,点P在l上,则有PA=PB.
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
A
B
l
┐
O
P
新知探究
如图,线段AB外任意一点P1到点A,点B的距离相等.求证:点P1在线段AB的垂直平分线上.
证明:过点P1作直线l,使得l⊥AB,垂足为O.
∵l⊥AB,
∴∠P1OA=∠P1OB=90°,
∵在Rt△P1AO和Rt△P1BO中,P1A=P1B,
P1O=P1O,
∴Rt△P1AO≌Rt△P1BO(HL).
∴AO=BO.
∵AO=BO,∠P1OA=∠P1OB=90°,
∴P1在线段AB的垂直平分线上.
A
B
l
┐
O
P1
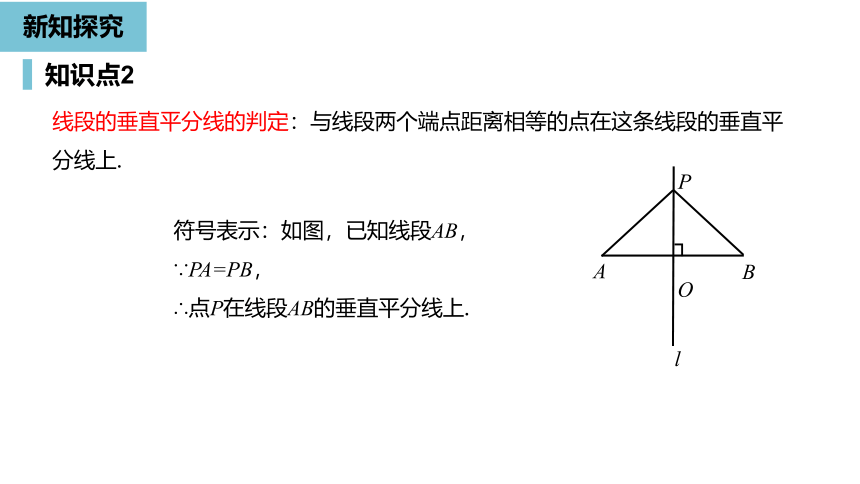
知识点2
新知探究
线段的垂直平分线的判定:与线段两个端点距离相等的点在这条线段的垂直平分线上.
符号表示:如图,已知线段AB,∵PA=PB,
∴点P在线段AB的垂直平分线上.
A
B
l
┐
O
P
新知探究
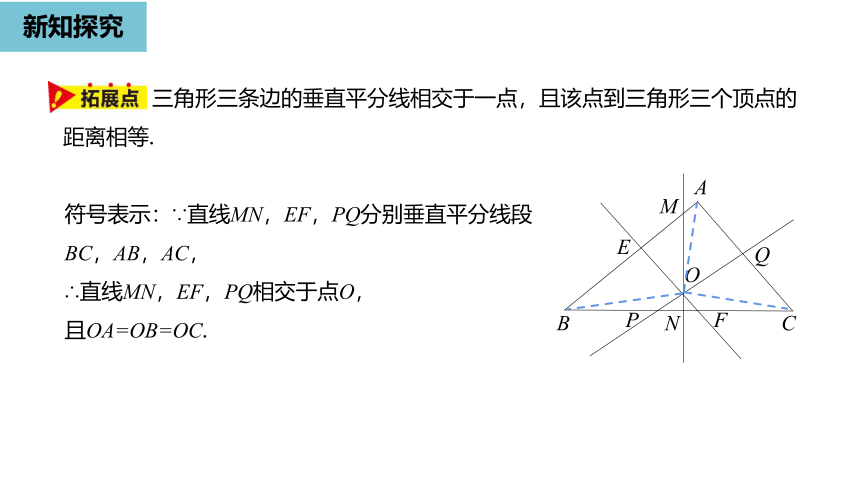
符号表示:∵直线MN,EF,PQ分别垂直平分线段BC,AB,AC,
∴直线MN,EF,PQ相交于点O,
且OA=OB=OC.
三角形三条边的垂直平分线相交于一点,且该点到三角形三个顶点的距离相等.
P
F
N
M
E
Q
O
B
C
A
新知探究
小结:从上面两个结论可以看出,在线段AB的垂直平分线l上的点与点A,B的距离都相等,反过来,与A,B的距离相等的点都在l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合.
A
B
l
┐
O
P
知识点3
新知探究
1、经过已知直线外一点作这条直线的垂线.
已知,直线AB和AB外一点C.
求作:AB的垂线,使它经过点C.
A
B
B
.
知识点3
新知探究
1、经过已知直线外一点作这条直线的垂线.
作法:(1)任意取一点K,使点K和点C在AB的两旁;
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E;
(3)分别以点D和点E为圆心,大于
DE的长为半径作弧,两弧相交于点F;
(4)作直线CF.
直线CF就是所求作的垂线.
新知探究
思考:直观上我们能感觉两个平面图形是成轴对称的,但是如何验证呢?在不折叠图形的情况下,你能准确地做出轴对称图形的对称轴吗?
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.
因此,只要能找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
新知探究
2、如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴,为此作出到点A、B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
?
?
A
B
新知探究
作法:如图所示:
(1)分别以点A和点B为圆心,大于
AB的长为半径作弧(想一想为什么),两弧线相交于C,D两点;
(2)作直线CD,即是所求作的直线.
?
?
A
B
C
D
2、如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
新知探究
3、作轴对称图形或成轴对称的两个图形的对称轴.
(1)作对称轴的依据:
如果一个图形是轴对称图形或两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.
(2)作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
找对应点时,一般找图形的顶点或转折点,这样做出的图形更准确.
新知探究
对于如图所示的五角星,可以选择一对对应点A和A′,连接AA′,
作出线段AA′的垂直平分线l,则l就是这个五角星的一条对称轴.
A
A′
l
找对应点时,一般找图形的顶点或转折点,这样做出的图形更准确.
类似的,请你尝试动手作出这个五角星的其他对称轴.
跟踪训练
新知探究
如图,直线AE是线段BC的垂直平分线,垂足为E,D为AE上一点,
求证:∠ABD=∠ACD.
证明:∵AE是线段BC的垂直平分线,D为AE上一点,
∴AB=AC,BD=DC.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴△ABD≌△ACD(SSS).
∴∠ABD=∠ACD.
E
B
C
D
A
跟踪训练
新知探究
如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
解:直线AM是线段BC的垂直平分线.
理由如下:
由AB=AC,MB=MC可知,点A,点M都在线段BC
的垂直平分线上.
根据“两点确定一条直线”,则直线AM就是线段
BC的垂直平分线.
B
C
M
A
随堂练习
1
如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?
解:AB=AC=CE,AB+BD=DE.
理由如下:
∵AD⊥BC,BD=DC,
∴AB=AC.
∵点C在AE的垂直平分线上,
∴AC=CE.
∴AB=AC=CE,AB+BD=CE+DC=DE,即AB+BD=DE.
C
┐
B
D
A
E
随堂练习
2
如图,在△ABC中,AB=5cm,BC的垂直平分线分别交AB,BC于点D,E,△ACD的周长为8cm,求线段AC的长.
解:∵DE为线段BC的垂直平分线,
∴CD=BD.
∴△ACD的周长为AC+AD+CD
=AC+AD+BD
=AC+AB
=8cm.
∵AB=5cm,
∴AC=3cm.
B
C
E
D
A
随堂练习
3
如图,四边形ABCD中,AB=AD,BC=DC,E是AC上的一点,连接DE,BE,
求证:∠ABE=∠ADE.
A
D
E
证明:连接DB.
∵AB=AD,BC=DC,
∴点A和点C都在线段BD的垂直平分线上.
∴线段AC所在的直线是线段BD的垂直平分线.
∵E是AC上的一点,
∴BE=DE.
在△ABE和△ADE中,AB=AD,
BE=DE,
AE=AE,
∴
△ABE≌△ADE.
∴∠ABE=∠ADE.
B
C
课堂小结
线段垂直
平分线
性质
判定
作对称轴
线段垂直平分线上的点与这条线段两个端点的距离相等
与线段两个端点距离相等的点在这条线段的垂直平分线上
尺规作图画一个轴对称图形或成轴对称图形的对称轴
拓展提升
1
如图,在△ABC中,直线DE是线段AC的垂直平分线,△ABC的周长为19cm,
△ABD的周长为13cm,则AE的长为(
).
证明:∵直线DE是线段AC的垂直平分线,
∴AD=DC,AE=CE=
AC.
∵△ABC的周长为19cm,△ABD的周长为13cm,
∴AB+BC+AC=19cm,AB+BD+AD=AB+BC=13cm.
∴AC=19cm-13cm=6cm.
6cm
E
C
B
D
A
13.1.3 垂直平分线
轴对称
知识回顾
1、线段是轴对称图形吗?它的对称轴是什么?
2、什么是线段的垂直平分线?
线段是轴对称图形,它的对称轴是这条线段的垂直平分线.
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
学习目标
1、理解并掌握线段垂直平分线的性质和判定的内容.
2、探究线段垂直平分线的性质和判定的过程.
3、熟练运用线段垂直平分线的性质和判定解决实际问题.
课堂导入
思考:如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,分别量一量点P1,P2,P3,……到点A和点B的距离,你有什么发现?
可以发现,点P1,P2,P3,……到点A的距离与它们到点B的距离分别相等,如果把线段AB沿着直线l对折,线段P1A与P1B,线段P2A与P2B,线段P3A与P3B……都是重合的,因此它们也分别相等.
A
B
l
┐
P1
P2
P3
课堂导入
证明:∵直线l垂直平分线段AB,
∴AO=BO,∠P1OA=∠P1OB=90°.
∵在△P1AO和△P1BO中,AO=BO,
∠P1OA=∠P1OB,
P1O=P1O,
∴△P1AO≌△P1BO(SAS).
∴P1A=P1B.
A
B
l
┐
P1
P2
P3
思考:如图,直线l垂直平分线段AB,P1,P2,P3,……是l上的点,分别量一量点P1,P2,P3,……到点A和点B的距离,你有什么发现?
知识点1
新知探究
线段的垂直平分线的性质:线段垂直平分线上的点与这条线段两个端点的距离相等.
符号表示:如图,直线l⊥AB,垂足为O,AO=BO,点P在l上,则有PA=PB.
反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
A
B
l
┐
O
P
新知探究
如图,线段AB外任意一点P1到点A,点B的距离相等.求证:点P1在线段AB的垂直平分线上.
证明:过点P1作直线l,使得l⊥AB,垂足为O.
∵l⊥AB,
∴∠P1OA=∠P1OB=90°,
∵在Rt△P1AO和Rt△P1BO中,P1A=P1B,
P1O=P1O,
∴Rt△P1AO≌Rt△P1BO(HL).
∴AO=BO.
∵AO=BO,∠P1OA=∠P1OB=90°,
∴P1在线段AB的垂直平分线上.
A
B
l
┐
O
P1
知识点2
新知探究
线段的垂直平分线的判定:与线段两个端点距离相等的点在这条线段的垂直平分线上.
符号表示:如图,已知线段AB,∵PA=PB,
∴点P在线段AB的垂直平分线上.
A
B
l
┐
O
P
新知探究
符号表示:∵直线MN,EF,PQ分别垂直平分线段BC,AB,AC,
∴直线MN,EF,PQ相交于点O,
且OA=OB=OC.
三角形三条边的垂直平分线相交于一点,且该点到三角形三个顶点的距离相等.
P
F
N
M
E
Q
O
B
C
A
新知探究
小结:从上面两个结论可以看出,在线段AB的垂直平分线l上的点与点A,B的距离都相等,反过来,与A,B的距离相等的点都在l上,所以直线l可以看成与两点A,B的距离相等的所有点的集合.
A
B
l
┐
O
P
知识点3
新知探究
1、经过已知直线外一点作这条直线的垂线.
已知,直线AB和AB外一点C.
求作:AB的垂线,使它经过点C.
A
B
B
.
知识点3
新知探究
1、经过已知直线外一点作这条直线的垂线.
作法:(1)任意取一点K,使点K和点C在AB的两旁;
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E;
(3)分别以点D和点E为圆心,大于
DE的长为半径作弧,两弧相交于点F;
(4)作直线CF.
直线CF就是所求作的垂线.
新知探究
思考:直观上我们能感觉两个平面图形是成轴对称的,但是如何验证呢?在不折叠图形的情况下,你能准确地做出轴对称图形的对称轴吗?
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.
因此,只要能找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.
新知探究
2、如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
分析:我们只要连接点A和点B,作出线段AB的垂直平分线,就可以得到点A和点B的对称轴,为此作出到点A、B距离相等的两点,即线段AB的垂直平分线上的两点,从而作出线段AB的垂直平分线.
?
?
A
B
新知探究
作法:如图所示:
(1)分别以点A和点B为圆心,大于
AB的长为半径作弧(想一想为什么),两弧线相交于C,D两点;
(2)作直线CD,即是所求作的直线.
?
?
A
B
C
D
2、如图,点A和点B关于某条直线成轴对称,你能试着作出这条直线吗?
新知探究
3、作轴对称图形或成轴对称的两个图形的对称轴.
(1)作对称轴的依据:
如果一个图形是轴对称图形或两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.
(2)作对称轴的步骤:
①找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
②连:连接这对对应点;
③作:做出对应点所连线段的垂直平分线.
找对应点时,一般找图形的顶点或转折点,这样做出的图形更准确.
新知探究
对于如图所示的五角星,可以选择一对对应点A和A′,连接AA′,
作出线段AA′的垂直平分线l,则l就是这个五角星的一条对称轴.
A
A′
l
找对应点时,一般找图形的顶点或转折点,这样做出的图形更准确.
类似的,请你尝试动手作出这个五角星的其他对称轴.
跟踪训练
新知探究
如图,直线AE是线段BC的垂直平分线,垂足为E,D为AE上一点,
求证:∠ABD=∠ACD.
证明:∵AE是线段BC的垂直平分线,D为AE上一点,
∴AB=AC,BD=DC.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴△ABD≌△ACD(SSS).
∴∠ABD=∠ACD.
E
B
C
D
A
跟踪训练
新知探究
如图,AB=AC,MB=MC,直线AM是线段BC的垂直平分线吗?
解:直线AM是线段BC的垂直平分线.
理由如下:
由AB=AC,MB=MC可知,点A,点M都在线段BC
的垂直平分线上.
根据“两点确定一条直线”,则直线AM就是线段
BC的垂直平分线.
B
C
M
A
随堂练习
1
如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB,AC,CE的长度有什么关系?AB+BD与DE有什么关系?
解:AB=AC=CE,AB+BD=DE.
理由如下:
∵AD⊥BC,BD=DC,
∴AB=AC.
∵点C在AE的垂直平分线上,
∴AC=CE.
∴AB=AC=CE,AB+BD=CE+DC=DE,即AB+BD=DE.
C
┐
B
D
A
E
随堂练习
2
如图,在△ABC中,AB=5cm,BC的垂直平分线分别交AB,BC于点D,E,△ACD的周长为8cm,求线段AC的长.
解:∵DE为线段BC的垂直平分线,
∴CD=BD.
∴△ACD的周长为AC+AD+CD
=AC+AD+BD
=AC+AB
=8cm.
∵AB=5cm,
∴AC=3cm.
B
C
E
D
A
随堂练习
3
如图,四边形ABCD中,AB=AD,BC=DC,E是AC上的一点,连接DE,BE,
求证:∠ABE=∠ADE.
A
D
E
证明:连接DB.
∵AB=AD,BC=DC,
∴点A和点C都在线段BD的垂直平分线上.
∴线段AC所在的直线是线段BD的垂直平分线.
∵E是AC上的一点,
∴BE=DE.
在△ABE和△ADE中,AB=AD,
BE=DE,
AE=AE,
∴
△ABE≌△ADE.
∴∠ABE=∠ADE.
B
C
课堂小结
线段垂直
平分线
性质
判定
作对称轴
线段垂直平分线上的点与这条线段两个端点的距离相等
与线段两个端点距离相等的点在这条线段的垂直平分线上
尺规作图画一个轴对称图形或成轴对称图形的对称轴
拓展提升
1
如图,在△ABC中,直线DE是线段AC的垂直平分线,△ABC的周长为19cm,
△ABD的周长为13cm,则AE的长为(
).
证明:∵直线DE是线段AC的垂直平分线,
∴AD=DC,AE=CE=
AC.
∵△ABC的周长为19cm,△ABD的周长为13cm,
∴AB+BC+AC=19cm,AB+BD+AD=AB+BC=13cm.
∴AC=19cm-13cm=6cm.
6cm
E
C
B
D
A
