人教版八年级数学上册13.2画轴对称图形课时2课件(23张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.2画轴对称图形课时2课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 442.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 09:32:59 | ||
图片预览





文档简介
(共23张PPT)
13.2.2 画轴对称图形
画轴对称图形
由一个平面图形可以得到与它关于一条直线l对称的图形,
这个图形与原图形的大小、形状完全相同.
知识回顾
1、轴对称变换.
2、轴对称变换的性质.
①新图形上的每一点都是原图形的某一点关于直线l的对称点;
②连接任意一对对应点的线段被对称轴垂直平分.
知识回顾
3、画轴对称图形.
找:在原图形上找特殊点(如线段端点等);
画:画出各个特殊点关于对称轴的对称点;
连:依次连接各对称点.
学习目标
1、理解在平面直角坐标系中,
已知点关于x轴、y轴对称的点的坐标的变化规律.
2、掌握在平面直角坐标系中作出一个图形的轴对称图形的方法.
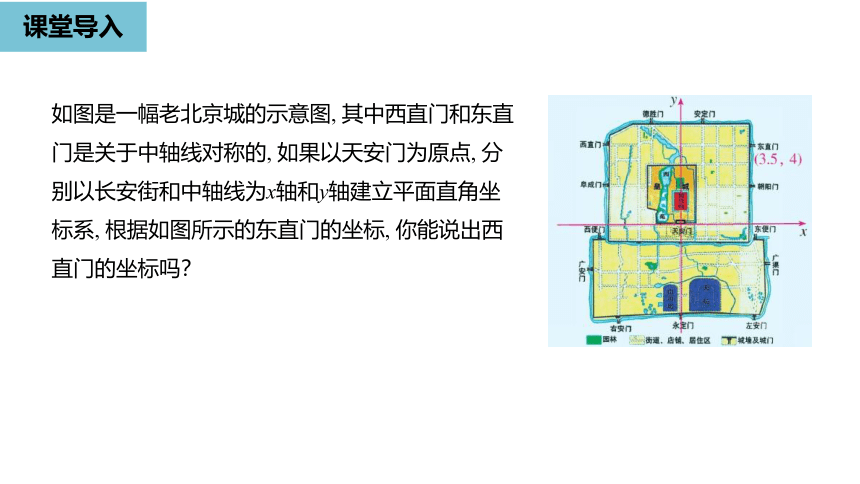
课堂导入
如图是一幅老北京城的示意图,
其中西直门和东直门是关于中轴线对称的,
如果以天安门为原点,
分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,
根据如图所示的东直门的坐标,
你能说出西直门的坐标吗?
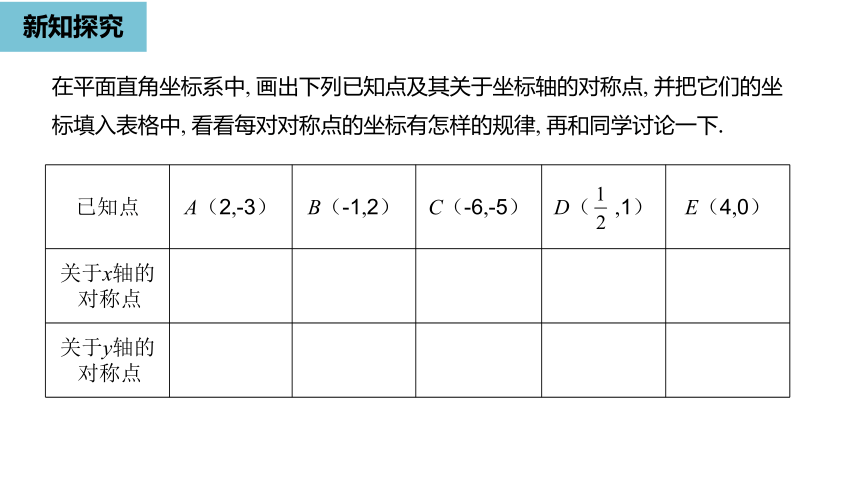
新知探究
在平面直角坐标系中,
画出下列已知点及其关于坐标轴的对称点,
并把它们的坐标填入表格中,
看看每对对称点的坐标有怎样的规律,
再和同学讨论一下.
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于x轴的
对称点
关于y轴的
对称点
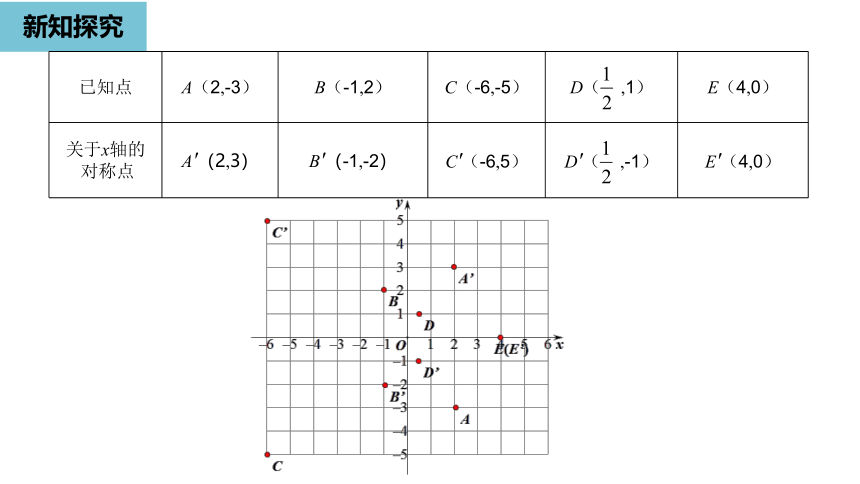
新知探究
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于x轴的
对称点
A′(2,3)
B′(-1,-2)
C′(-6,5)
D′(
,-1)
E′(4,0)
新知探究
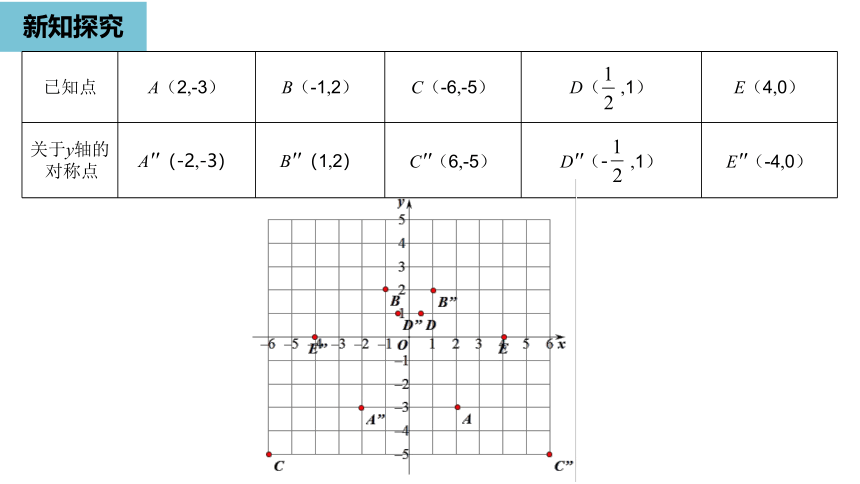
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于y轴的
对称点
A′′(-2,-3)
B′′(1,2)
C′′(6,-5)
D′′(
,1)
E′′(-4,0)
新知探究
根据表格所填的坐标,
你发现了什么规律
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于x轴的
对称点
A′(2,3)
B′(-1,-2)
C′(-6,5)
D′(
,-1)
E′(4,0)
关于y轴的
对称点
A′′(-2,-3)
B′′(1,2)
C′′(6,-5)
D′′(
,1)
E′′(-4,0)
新知探究
关于坐标轴对称的点的坐标规律
1、点(x,y)关于x轴对称的点的坐标是(x,-y),
特点是横坐标相同,
纵坐标互为相反数.
2、点(x,y)关于y轴对称的点的坐标是(-x,y),
特点是纵坐标相同,
横坐标互为相反数.
知识点1
新知探究
知识点1
对称点坐标要记牢,
相反数位置莫混淆;
x轴对称横坐标相同,
y轴对称纵坐标相同.
新知探究
在直角坐标系中画与已知图形关于某直线成轴对称的图形的方法:
计算:计算出已知图形中的一些特殊点的对称点的坐标;
描点:根据对称点的坐标描点;
连接:按原图对应点连接所描各点得到对称图形.
知识点2
所找的特殊点一定要能确定原图形,
否则画出的图形与原图形不一定成轴对称.
新知探究
如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),
B(-2,1),
C(-2,5),
D(-5,4),
分别画出与四边形ABCD关于x轴和y轴对称的图形.
新知探究
已知点
A(-5,1)
B(-2,1)
C(-2,5)
D(-5,4)
关于x轴的
对称点
A′(-5,-1)
B′(-2,-1)
C′(-2,-5)
D′(-5,-4)
新知探究
已知点
A(-5,1)
B(-2,1)
C(-2,5)
D(-5,4)
关于y轴的
对称点
A′′(5,1)
B′′(2,1)
C′′(2,5)
D′′(5,4)
跟踪训练
新知探究
1、分别写出下列各点关于x轴和y轴对称的点的坐标.
(-2,6),
(1,-2),
(-1,3),
(-4,-2),
(1,0)
关于x轴对称的点的坐标为:
(-2,-6),
(1,2),
(-1,-3),
(-4,2),
(1,0)
关于y轴对称的点的坐标为:
(2,6),
(-1,-2),
(1,3),
(4,-2),
(-1,0)
在平面直角坐标系中,
点B的坐标是(4,-1),
点A与点B关于x轴对称,
则点A的坐标是(
)
A.(4,1)
B.(-1,4)
C.(-4,-1)
D.(-1,-4)
随堂练习
1
分析:点A与点B关于x轴对称,
则横坐标相同,
纵坐标相反,
点B的坐标为
(4,-1),
则点A的坐标为(4,1).
A
若点A(m,2)与点B(3,n)关于x轴对称,
则m+n的值是(
)
A.1
B.-2
C.2
D.5
随堂练习
2
分析:点A与点B关于x轴对称,
则横坐标相同,
纵坐标相反,
点A的坐标为
(m,2),
则点B的坐标为(3,n).
则m=3,
n=-2,
m+n=3+(-2)=1.
A
课堂小结
画轴对称图形
点(x,y)关于x轴
对称
点(x,y)关于y轴
对称
在直角坐标系中画出已知图形关于某条直线成轴对称图形的方法
横坐标相同
纵坐标相反
纵坐标相同
横坐标相反
计算、描点、连接
拓展提升
1
在平面直角坐标系中,
△ABC的顶点坐标分别为A(-4,1),
B(-2,1),
C(-2,3).
(1)作△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向下平移4个单位长度;
做出平移后的△A2B2C2;
(3)求四边形AA2B2C的面积.
拓展提升
1
(1)△ABC的顶点坐标分别为A(-4,1),
B(-2,1),
C(-2,3),
关于y轴对称的点分别为A1(4,1),
B1(2,1),
C1(2,3).
拓展提升
1
(2)△ABC的顶点坐标分别为A(-4,1),
B(-2,1),
C(-2,3),
向下平移4个单位长度的点分别为A1(-4,-3),
B1(-2,-3),
C1(-2,-1).
拓展提升
1
(3)四边形AA2B2C为梯形,
其中上底AA2=4,
下底B2C=6,
高A2B2=2,
所以四边形AA2B2C的面积为10.
13.2.2 画轴对称图形
画轴对称图形
由一个平面图形可以得到与它关于一条直线l对称的图形,
这个图形与原图形的大小、形状完全相同.
知识回顾
1、轴对称变换.
2、轴对称变换的性质.
①新图形上的每一点都是原图形的某一点关于直线l的对称点;
②连接任意一对对应点的线段被对称轴垂直平分.
知识回顾
3、画轴对称图形.
找:在原图形上找特殊点(如线段端点等);
画:画出各个特殊点关于对称轴的对称点;
连:依次连接各对称点.
学习目标
1、理解在平面直角坐标系中,
已知点关于x轴、y轴对称的点的坐标的变化规律.
2、掌握在平面直角坐标系中作出一个图形的轴对称图形的方法.
课堂导入
如图是一幅老北京城的示意图,
其中西直门和东直门是关于中轴线对称的,
如果以天安门为原点,
分别以长安街和中轴线为x轴和y轴建立平面直角坐标系,
根据如图所示的东直门的坐标,
你能说出西直门的坐标吗?
新知探究
在平面直角坐标系中,
画出下列已知点及其关于坐标轴的对称点,
并把它们的坐标填入表格中,
看看每对对称点的坐标有怎样的规律,
再和同学讨论一下.
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于x轴的
对称点
关于y轴的
对称点
新知探究
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于x轴的
对称点
A′(2,3)
B′(-1,-2)
C′(-6,5)
D′(
,-1)
E′(4,0)
新知探究
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于y轴的
对称点
A′′(-2,-3)
B′′(1,2)
C′′(6,-5)
D′′(
,1)
E′′(-4,0)
新知探究
根据表格所填的坐标,
你发现了什么规律
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
D(
,1)
E(4,0)
关于x轴的
对称点
A′(2,3)
B′(-1,-2)
C′(-6,5)
D′(
,-1)
E′(4,0)
关于y轴的
对称点
A′′(-2,-3)
B′′(1,2)
C′′(6,-5)
D′′(
,1)
E′′(-4,0)
新知探究
关于坐标轴对称的点的坐标规律
1、点(x,y)关于x轴对称的点的坐标是(x,-y),
特点是横坐标相同,
纵坐标互为相反数.
2、点(x,y)关于y轴对称的点的坐标是(-x,y),
特点是纵坐标相同,
横坐标互为相反数.
知识点1
新知探究
知识点1
对称点坐标要记牢,
相反数位置莫混淆;
x轴对称横坐标相同,
y轴对称纵坐标相同.
新知探究
在直角坐标系中画与已知图形关于某直线成轴对称的图形的方法:
计算:计算出已知图形中的一些特殊点的对称点的坐标;
描点:根据对称点的坐标描点;
连接:按原图对应点连接所描各点得到对称图形.
知识点2
所找的特殊点一定要能确定原图形,
否则画出的图形与原图形不一定成轴对称.
新知探究
如图,四边形ABCD的四个顶点的坐标分别为A(-5,1),
B(-2,1),
C(-2,5),
D(-5,4),
分别画出与四边形ABCD关于x轴和y轴对称的图形.
新知探究
已知点
A(-5,1)
B(-2,1)
C(-2,5)
D(-5,4)
关于x轴的
对称点
A′(-5,-1)
B′(-2,-1)
C′(-2,-5)
D′(-5,-4)
新知探究
已知点
A(-5,1)
B(-2,1)
C(-2,5)
D(-5,4)
关于y轴的
对称点
A′′(5,1)
B′′(2,1)
C′′(2,5)
D′′(5,4)
跟踪训练
新知探究
1、分别写出下列各点关于x轴和y轴对称的点的坐标.
(-2,6),
(1,-2),
(-1,3),
(-4,-2),
(1,0)
关于x轴对称的点的坐标为:
(-2,-6),
(1,2),
(-1,-3),
(-4,2),
(1,0)
关于y轴对称的点的坐标为:
(2,6),
(-1,-2),
(1,3),
(4,-2),
(-1,0)
在平面直角坐标系中,
点B的坐标是(4,-1),
点A与点B关于x轴对称,
则点A的坐标是(
)
A.(4,1)
B.(-1,4)
C.(-4,-1)
D.(-1,-4)
随堂练习
1
分析:点A与点B关于x轴对称,
则横坐标相同,
纵坐标相反,
点B的坐标为
(4,-1),
则点A的坐标为(4,1).
A
若点A(m,2)与点B(3,n)关于x轴对称,
则m+n的值是(
)
A.1
B.-2
C.2
D.5
随堂练习
2
分析:点A与点B关于x轴对称,
则横坐标相同,
纵坐标相反,
点A的坐标为
(m,2),
则点B的坐标为(3,n).
则m=3,
n=-2,
m+n=3+(-2)=1.
A
课堂小结
画轴对称图形
点(x,y)关于x轴
对称
点(x,y)关于y轴
对称
在直角坐标系中画出已知图形关于某条直线成轴对称图形的方法
横坐标相同
纵坐标相反
纵坐标相同
横坐标相反
计算、描点、连接
拓展提升
1
在平面直角坐标系中,
△ABC的顶点坐标分别为A(-4,1),
B(-2,1),
C(-2,3).
(1)作△ABC关于y轴对称的△A1B1C1;
(2)将△ABC向下平移4个单位长度;
做出平移后的△A2B2C2;
(3)求四边形AA2B2C的面积.
拓展提升
1
(1)△ABC的顶点坐标分别为A(-4,1),
B(-2,1),
C(-2,3),
关于y轴对称的点分别为A1(4,1),
B1(2,1),
C1(2,3).
拓展提升
1
(2)△ABC的顶点坐标分别为A(-4,1),
B(-2,1),
C(-2,3),
向下平移4个单位长度的点分别为A1(-4,-3),
B1(-2,-3),
C1(-2,-1).
拓展提升
1
(3)四边形AA2B2C为梯形,
其中上底AA2=4,
下底B2C=6,
高A2B2=2,
所以四边形AA2B2C的面积为10.
