人教版八年级数学上册第13.2画轴对称图形课时1课件(25张PPT)
文档属性
| 名称 | 人教版八年级数学上册第13.2画轴对称图形课时1课件(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 274.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 09:34:24 | ||
图片预览








文档简介
(共25张PPT)
13.2.1 画轴对称图形
画轴对称图形
知识回顾
1、线段垂直平分线的性质.
2、线段垂直平分线的判定.
线段垂直平分线上的点与这条线段的两个端点的距离相等.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
知识回顾
3、作轴对称图形或成轴对称的两个图形的对称轴.
找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
连:连接这一对对应点;
作:作出对应点所连线段的垂直平分线.
学习目标
1、理解图形轴对称变换的性质.
2、能够按照要求画出一个平面图形关于某条直线对称
的图形.
课堂导入
如图,在一张半透明的纸的左边部分,画一只左脚印.把这张纸对折后描图,打开对折的纸,就能够得到相应的右脚印.这时,右脚印和左脚印成轴对称,折痕所在直线就是它们的对称轴,并且连接任意一对对应点的线段被对称轴垂直平分.
请你动手再画一个图形,看看能否得到相同的结论.
知识点1
新知探究
1、轴对称变换:由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同.
2、轴对称变换的性质:新图形上的每一点都是原图形上的某一点关于直线l的对称点;连接任意一对对应点的线段被对称轴垂直平分.
思考:如果有一个图形和一条线段,如何画出与这个图形关于这条直线对称的图形呢?
新知探究
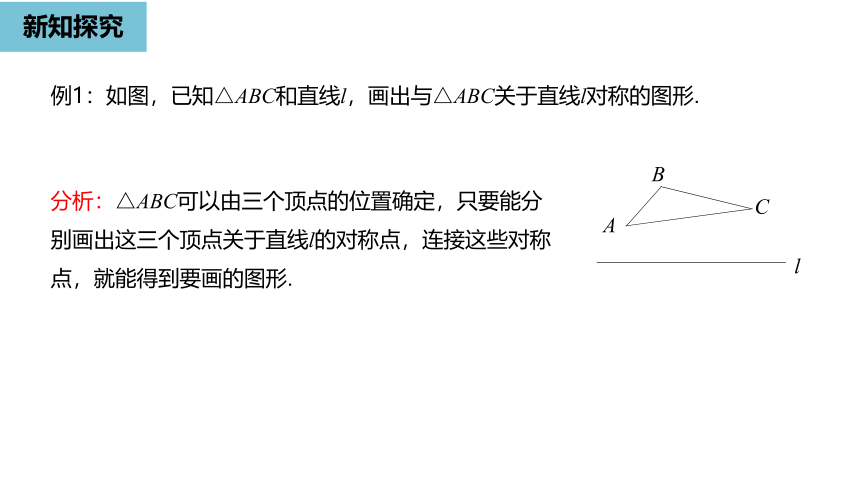
例1:如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
l
C
A
B
新知探究
思考1:已知点A和直线l,画出点A关于直线l的对称点A′.
过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
l
A
?
?
A′
┐
O
新知探究
l
B
思考2:已知线段AB和直线l,画出线段AB关于直线l的对称线段A′B′.
(1)过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
(2)过点B作直线l的垂线,垂足为P,在垂线上截取PB′=PB,点B′就是点B关于直线l的对称点.
(3)连接A′、B′,则线段A′B′即是所画.
A′
B′
A
O
.
P
.
┐
┐
新知探究
例1:如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
作法:(1)如图,过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′.
(3)连接A′B′,B′C′,C′A′,则△A′B′C′即为所求.
l
C
C′
A′
┐
B′
B
A
O
.
.
.
新知探究
几何图形都可以看作由点组成,对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
如图,五边形ABCDE可以由五个顶点的位置确定大小、形状,只要能够画出五个顶点A,B,C,D,E分别关于直线l的对称点,顺次连接五个对称点得到的五边形即为所画的轴对称图形.
知识点2
E
A
B
D
C
l
新知探究
画轴对称图形的方法可以归纳为“一找、二画、三连”:
找:在原图形上找特殊点(如线段端点);
画:画出各个特殊点关于对称轴的对称点;
连:依次连接各对称点;
连接这些对称点,就可以得到原图形的轴对称图形.
知识点2
新知探究
(1)特殊点对画轴对称图形特别重要,找特殊点时,要把确定图形形状的特殊点找全,否则画出的图形将不准确或不完整.
(2)常见的特殊点,除线段的端点外,还有线与线的交点、中点等.
跟踪训练
新知探究
如图,△ABC是由△DEF经过轴对称变换得到的,直线l是对称轴.
(1)△ABC与△DEF全等吗?全等的两个图形一定可以通过轴对称变换得到吗?
(2)分别找出点B,C关于直线l的对称点,如果点M在△ABC内,那么点M关于直线l的对称点一定在△DEF内吗?
(3)连接AD,线段AD与直线l有什么关系?
跟踪训练
新知探究
如图,△ABC是由△DEF经过轴对称变换得到的,直线l是对称轴.
(1)△ABC与△DEF全等.全等的两个图形不一定可以通过轴对称变换得到.
(2)点B,C关于直线l的对称点分别是点E,F;点M关于直线l的对称点一定在△DEF内.
(3)线段AD被直线l垂直平分.
如图,把下列图形补成关于直线l对称的图形.
l
l
l
随堂练习
1
l
l
l
作轴对称图形的口诀:作垂线,截等线,顺次连.
随堂练习
1
随堂练习
2
用纸片剪一个三角形,分别沿着它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些部分不能重合?
沿中线对折
沿高对折
沿角平分线对折
随堂练习
3
已知,一个车牌号码在水中的倒影如图所示,则该车牌号为
(
).
分析:根据生活经验可知,物体与其在水中的倒影关于水面成轴对称,因此在倒影的下面画一条水平直线,然后作出倒影关于这条直线成轴对称的图形即可.
FM5379
课堂小结
画轴对称图形
轴对称变换
轴对称变换的性质
画出已知图形的轴对称图形
成轴对称的两个图形全等
1、新旧图形的对应点是对称点
2、连接对应点的线段被对称轴垂直平分
一找,二画,三连
拓展提升
1
如图,有一孩童在A处放牛,其家住在B处,A,B到河岸的距离分别为AC,BD,且AC=BD,若A到河岸CD的中点的距离为600m.
(1)孩童从A处把牛牵到河边饮水后再回家,试问在何处饮水,他所走的路程最短?请在图上标注出该处,并说明理由.
(2)你知道最短路程为多少吗?
河岸
?
?
A
B
C
D
拓展提升
1
如图,有一孩童在A处放牛,其家住在B处,A,B到河岸的距离分别为AC,BD,且AC=BD,若A到河岸CD的中点的距离为600m.
分析:已知直线CD和与直线CD同侧的两点A,B,求在CD上找一点M,使得AM+BM的长度最短.
河岸
?
?
A
B
C
D
拓展提升
1
解:(1)①作点A关于CD的对称点A′.
②连接A′B交CD于点M,则点M即为所求的点.
河岸
?
?
A
B
C
D
M
A′
你能证明点M就是使得AM+BM最短的点吗
拓展提升
1
解:(1)
在CD上取得任意一点M′,连接AM′,A′M′,BM′.
∵直线CD是A,A′的对称轴,点M,M′在CD上,
∴AM=A′M,AM′=A′M′.
∴AM+BM=A′M+BM=A′B.
∵在△A′M′B中,A′M′+BM′>A′B,
∴AM′+BM′>A′B.
∵
A′B=A′M+BM=AM+BM,
∴AM′+BM′>AM+BM.
则点M即为CD上使得AM+BM最短的点.
河岸
?
?
A
B
C
D
M
A′
M’
拓展提升
1
解:(2)
由(1)可得,AM=A′M,AC=A′C=BD.
在△A′MC和△BMD中,∠A′MC=∠BMD,
∠A′CM=∠BDM=90°,
A′C=BD,
∴△A′MC≌△BMD(AAS).
∴A′M=BM,CM=DM.
∴M是CD的中点,
∵AM=600m,
∴A′B=A′M+BM=AM+BM=2AM
=1200m.
河岸
?
?
A
B
C
D
M
A′
13.2.1 画轴对称图形
画轴对称图形
知识回顾
1、线段垂直平分线的性质.
2、线段垂直平分线的判定.
线段垂直平分线上的点与这条线段的两个端点的距离相等.
与线段两个端点距离相等的点在这条线段的垂直平分线上.
知识回顾
3、作轴对称图形或成轴对称的两个图形的对称轴.
找:找到轴对称图形或成轴对称的两个图形的任意一对对应点;
连:连接这一对对应点;
作:作出对应点所连线段的垂直平分线.
学习目标
1、理解图形轴对称变换的性质.
2、能够按照要求画出一个平面图形关于某条直线对称
的图形.
课堂导入
如图,在一张半透明的纸的左边部分,画一只左脚印.把这张纸对折后描图,打开对折的纸,就能够得到相应的右脚印.这时,右脚印和左脚印成轴对称,折痕所在直线就是它们的对称轴,并且连接任意一对对应点的线段被对称轴垂直平分.
请你动手再画一个图形,看看能否得到相同的结论.
知识点1
新知探究
1、轴对称变换:由一个平面图形可以得到与它关于一条直线l对称的图形,这个图形与原图形的形状、大小完全相同.
2、轴对称变换的性质:新图形上的每一点都是原图形上的某一点关于直线l的对称点;连接任意一对对应点的线段被对称轴垂直平分.
思考:如果有一个图形和一条线段,如何画出与这个图形关于这条直线对称的图形呢?
新知探究
例1:如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
分析:△ABC可以由三个顶点的位置确定,只要能分别画出这三个顶点关于直线l的对称点,连接这些对称点,就能得到要画的图形.
l
C
A
B
新知探究
思考1:已知点A和直线l,画出点A关于直线l的对称点A′.
过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
l
A
?
?
A′
┐
O
新知探究
l
B
思考2:已知线段AB和直线l,画出线段AB关于直线l的对称线段A′B′.
(1)过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,点A′就是点A关于直线l的对称点.
(2)过点B作直线l的垂线,垂足为P,在垂线上截取PB′=PB,点B′就是点B关于直线l的对称点.
(3)连接A′、B′,则线段A′B′即是所画.
A′
B′
A
O
.
P
.
┐
┐
新知探究
例1:如图,已知△ABC和直线l,画出与△ABC关于直线l对称的图形.
作法:(1)如图,过点A作直线l的垂线,垂足为O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′.
(3)连接A′B′,B′C′,C′A′,则△A′B′C′即为所求.
l
C
C′
A′
┐
B′
B
A
O
.
.
.
新知探究
几何图形都可以看作由点组成,对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
如图,五边形ABCDE可以由五个顶点的位置确定大小、形状,只要能够画出五个顶点A,B,C,D,E分别关于直线l的对称点,顺次连接五个对称点得到的五边形即为所画的轴对称图形.
知识点2
E
A
B
D
C
l
新知探究
画轴对称图形的方法可以归纳为“一找、二画、三连”:
找:在原图形上找特殊点(如线段端点);
画:画出各个特殊点关于对称轴的对称点;
连:依次连接各对称点;
连接这些对称点,就可以得到原图形的轴对称图形.
知识点2
新知探究
(1)特殊点对画轴对称图形特别重要,找特殊点时,要把确定图形形状的特殊点找全,否则画出的图形将不准确或不完整.
(2)常见的特殊点,除线段的端点外,还有线与线的交点、中点等.
跟踪训练
新知探究
如图,△ABC是由△DEF经过轴对称变换得到的,直线l是对称轴.
(1)△ABC与△DEF全等吗?全等的两个图形一定可以通过轴对称变换得到吗?
(2)分别找出点B,C关于直线l的对称点,如果点M在△ABC内,那么点M关于直线l的对称点一定在△DEF内吗?
(3)连接AD,线段AD与直线l有什么关系?
跟踪训练
新知探究
如图,△ABC是由△DEF经过轴对称变换得到的,直线l是对称轴.
(1)△ABC与△DEF全等.全等的两个图形不一定可以通过轴对称变换得到.
(2)点B,C关于直线l的对称点分别是点E,F;点M关于直线l的对称点一定在△DEF内.
(3)线段AD被直线l垂直平分.
如图,把下列图形补成关于直线l对称的图形.
l
l
l
随堂练习
1
l
l
l
作轴对称图形的口诀:作垂线,截等线,顺次连.
随堂练习
1
随堂练习
2
用纸片剪一个三角形,分别沿着它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些部分不能重合?
沿中线对折
沿高对折
沿角平分线对折
随堂练习
3
已知,一个车牌号码在水中的倒影如图所示,则该车牌号为
(
).
分析:根据生活经验可知,物体与其在水中的倒影关于水面成轴对称,因此在倒影的下面画一条水平直线,然后作出倒影关于这条直线成轴对称的图形即可.
FM5379
课堂小结
画轴对称图形
轴对称变换
轴对称变换的性质
画出已知图形的轴对称图形
成轴对称的两个图形全等
1、新旧图形的对应点是对称点
2、连接对应点的线段被对称轴垂直平分
一找,二画,三连
拓展提升
1
如图,有一孩童在A处放牛,其家住在B处,A,B到河岸的距离分别为AC,BD,且AC=BD,若A到河岸CD的中点的距离为600m.
(1)孩童从A处把牛牵到河边饮水后再回家,试问在何处饮水,他所走的路程最短?请在图上标注出该处,并说明理由.
(2)你知道最短路程为多少吗?
河岸
?
?
A
B
C
D
拓展提升
1
如图,有一孩童在A处放牛,其家住在B处,A,B到河岸的距离分别为AC,BD,且AC=BD,若A到河岸CD的中点的距离为600m.
分析:已知直线CD和与直线CD同侧的两点A,B,求在CD上找一点M,使得AM+BM的长度最短.
河岸
?
?
A
B
C
D
拓展提升
1
解:(1)①作点A关于CD的对称点A′.
②连接A′B交CD于点M,则点M即为所求的点.
河岸
?
?
A
B
C
D
M
A′
你能证明点M就是使得AM+BM最短的点吗
拓展提升
1
解:(1)
在CD上取得任意一点M′,连接AM′,A′M′,BM′.
∵直线CD是A,A′的对称轴,点M,M′在CD上,
∴AM=A′M,AM′=A′M′.
∴AM+BM=A′M+BM=A′B.
∵在△A′M′B中,A′M′+BM′>A′B,
∴AM′+BM′>A′B.
∵
A′B=A′M+BM=AM+BM,
∴AM′+BM′>AM+BM.
则点M即为CD上使得AM+BM最短的点.
河岸
?
?
A
B
C
D
M
A′
M’
拓展提升
1
解:(2)
由(1)可得,AM=A′M,AC=A′C=BD.
在△A′MC和△BMD中,∠A′MC=∠BMD,
∠A′CM=∠BDM=90°,
A′C=BD,
∴△A′MC≌△BMD(AAS).
∴A′M=BM,CM=DM.
∴M是CD的中点,
∵AM=600m,
∴A′B=A′M+BM=AM+BM=2AM
=1200m.
河岸
?
?
A
B
C
D
M
A′
