人教版八年级数学上册13.3等腰三角形课时1课件(25张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.3等腰三角形课时1课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 176.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
13.3.1 等边三角形
等腰三角形
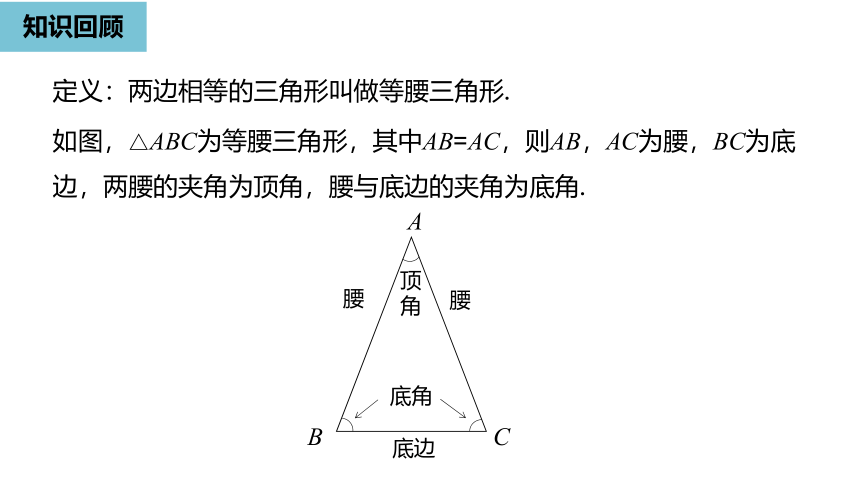
知识回顾
定义:两边相等的三角形叫做等腰三角形.
如图,△ABC为等腰三角形,其中AB=AC,则AB,AC为腰,BC为底边,两腰的夹角为顶角,腰与底边的夹角为底角.
A
B
C
腰
腰
底边
顶
角
底角
学习目标
1、了解等腰三角形的性质,体会等腰三角形“三线合一”的意义.
2、探索并掌握等腰三角形的性质,并用以解决实际问题.
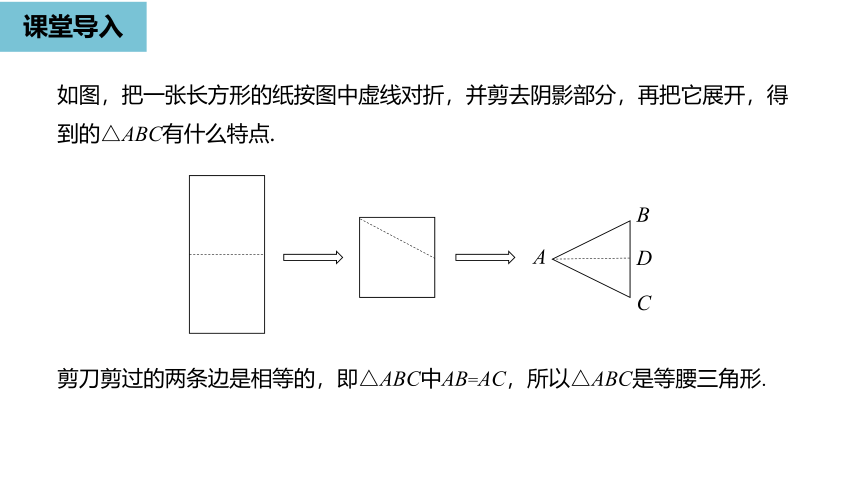
课堂导入
如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点.
剪刀剪过的两条边是相等的,即△ABC中AB=AC,所以△ABC是等腰三角形.
A
C
B
D
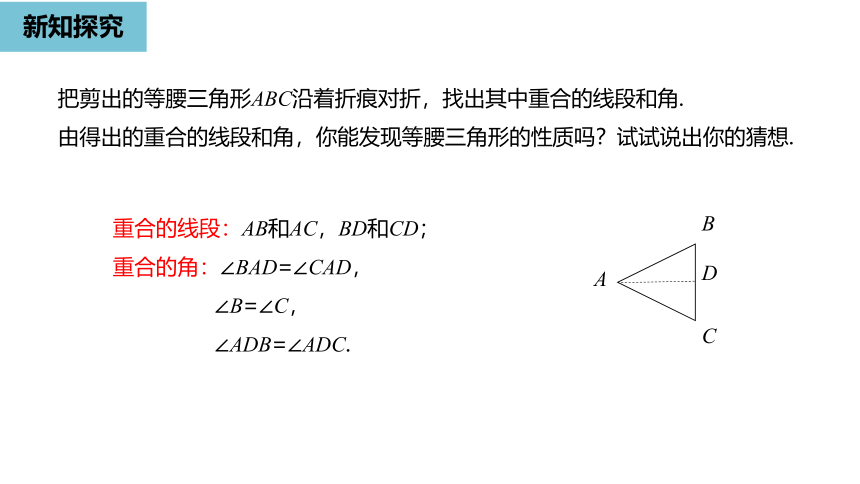
新知探究
把剪出的等腰三角形ABC沿着折痕对折,找出其中重合的线段和角.
由得出的重合的线段和角,你能发现等腰三角形的性质吗?试试说出你的猜想.
重合的线段:AB和AC,BD和CD;
重合的角:∠BAD=∠CAD,
∠B=∠C,
∠ADB=∠ADC.
A
C
B
D
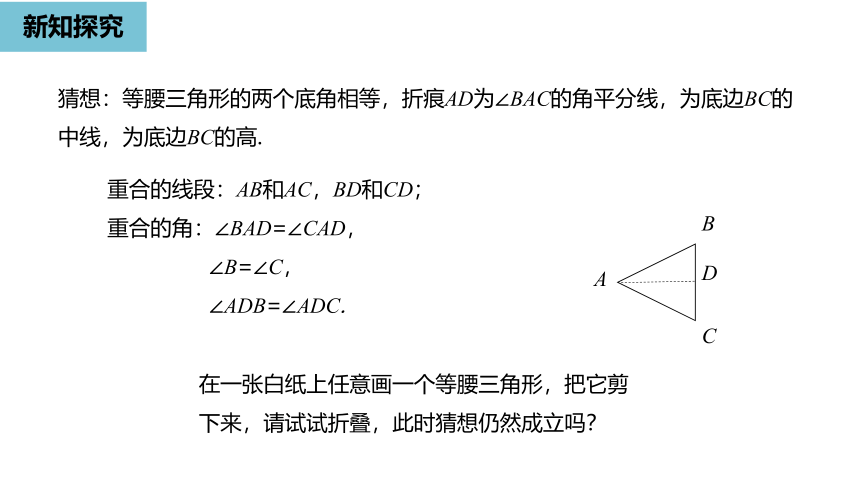
新知探究
猜想:等腰三角形的两个底角相等,折痕AD为∠BAC的角平分线,为底边BC的中线,为底边BC的高.
重合的线段:AB和AC,BD和CD;
重合的角:∠BAD=∠CAD,
∠B=∠C,
∠ADB=∠ADC.
在一张白纸上任意画一个等腰三角形,把它剪下来,请试试折叠,此时猜想仍然成立吗?
A
C
B
D
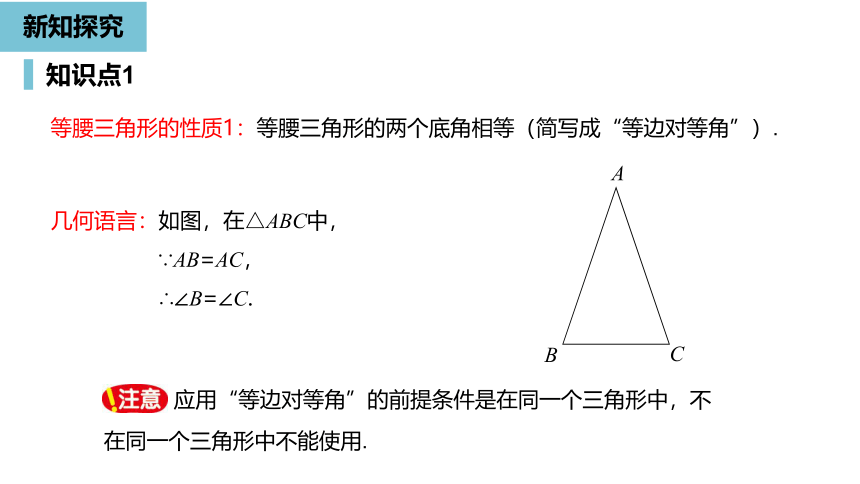
应用“等边对等角”的前提条件是在同一个三角形中,不在同一个三角形中不能使用.
新知探究
等腰三角形的性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
知识点1
几何语言:如图,在△ABC中,
∵AB=AC,
∴∠B=∠C.
A
B
C
新知探究
知识点1
(1)“等边对等角”是证明三角形中两个角相等的常用方法,这种方法比利用三角形全等证明两个角相等更方便.
(2)在等腰三角形中,依据三角形内角和等于180°,可以由顶角求底角,也可以由底角求顶角,且注意:如果已知条件中未说明是顶角还是底角时,要考虑所有可能的情况并分类讨论.
新知探究
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).
知识点2
几何语言:如图,在△ABC中,
①∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD.
②∵AB=AC,AD⊥BC,
∴AD平分∠BAC
,BD=CD.
③∵AB=AC,BD=CD,
∴AD平分∠BAC,AD⊥BC.
你能不能证明①②③的结论?
B
C
D
A
新知探究
知识点2
如图,在△ABC中,AB=AC,AD平分∠BAC,
求证:AD⊥BC,∠ADB=∠ADC
.
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(SAS).
∴∠BAD=∠CAD,∠ADB=∠ADC.
∵
∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC.
B
C
D
A
新知探究
知识点2
如图,在△ABC中,AB=AC,AD是底边BC的中线,
求证:AD⊥BC,AD平分∠BAC.
证明:∵AD是底边BC的中线,
∴BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴△ABD≌△ACD(SSS).
∴BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
∴AD平分∠BAC.
∵
∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC.
B
C
D
A
新知探究
知识点2
如图,在△ABC中,AB=AC,AD是底边BC的高,
求证:∠BAD=∠CAD
,BD=CD.
证明:∵AD是底边BC的高,
∴∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,AB=AC,
AD=AD,
∴Rt△ABD≌Rt△ACD(HL).
∴BD=CD,∠BAD=∠CAD
.
B
C
D
A
新知探究
知识点2
(1)“三线合一”的性质应用非常广泛,可以用来证明角相等、线段相等或线段垂直.
(2)等腰三角形是轴对称图形,对称轴为顶角平分线(或底边上的高或底边上的中线)所在的直线.
应用“三线合一”的前提条件是等腰三角形,且必须是底边上的中线、底边上的高和顶角的平分线才能互相重合.
新知探究
知识点2
等腰三角形的其他性质:
(1)等腰三角形两腰上的中线相等,两腰上的高相等,两底角的平分线也相等.
(2)等腰三角形底边上的任意一点到两腰的距离之和等于一腰上的高.
(3)等腰三角形底边上的高(或底边上的中线或顶角平分线)上任意一点到两腰的距离相等.
解:∵AB=AC,∠BAC=90°
,
∴∠B=∠C=45°.
∵AB=AC,AD是底边BC上的高,
∴AD是∠BAC的平分线,则∠BAD=∠DAC=45°.
∴AD是底边BC上的中线,则BD=CD.
跟踪训练
新知探究
如图,△ABC是等腰三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,请写出∠B,∠C,∠BAD,∠DAC的度数,并说明BD=CD.
A
B
C
┐
┐
跟踪训练
新知探究
如图,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为(
)
A.35°
B.45°
C.55°
D.60°
解:∵AB=AC,D为BC的中点,
∴∠B=∠C,AD⊥BC.
∵∠B=90°-∠BAD=55°,
∴∠C=55°.
C
如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为(
)
A.40°
B.36°
C.80°
D.25°
随堂练习
1
解:∵AB=AC,
∴∠C=∠B.
∵BD=BA,DA=DC,
∴∠BAD=∠BDA=2∠C=2∠B.
设∠C=∠B=x,则∠BAD=∠BDA=2x.
∵∠B+∠BAD+∠BDA=180°,
∴x=36°.
∴∠B=36°.
B
如图,AB//CD,AD=CD,∠1=65°,则∠2的度数为(
)
A.50°
B.60°
C.65°
D.70°
随堂练习
2
解:∵AB//CD,∠1=65°,
∴∠ACD=∠1=65°.
∵AD=CD,
∴∠DCA=∠DAC=65°.
∴∠2的度数为:180°-
65°-65°=50°.
A
随堂练习
3
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
D
解:∵∠BAD=26°,AB=AD,
∴∠B=∠ADB=
(180°-26°)=77°.
∵AD=CD,
∴∠C=∠DAC.
∵∠ADB=77°,∠ADB=∠C+∠DAC,
∴∠C的度数为
∠ADB=38.5°.
B
A
C
课堂小结
等腰
三角形
定义
性质
有两边相等的三角形
等边对等角
三线合一
拓展提升
1
(1)已知一个等腰三角形的一个内角是130°,它的另外两个内角是多少度?
(2)已知一个等腰三角形的一个内角是40°,它的另外两个内角是多少度?
(3)已知一个等腰三角形的两条边的长度比是3:2,且有一条边的长为12厘米,这个等腰三角形的周长最大是多少?
拓展提升
1
(1)已知一个等腰三角形的一个内角是130°,它的另外两个内角是多少度?
解:因为等腰三角形的两个底角相等,
所以这个已知的角只能是顶角,
则两个底角的度数都是
(180°-130°)=25°,
所以另外两个内角的度数分别为25°,25°.
拓展提升
1
(2)已知一个等腰三角形的一个内角是40°,它的另外两个内角是多少度?
解:①当已知角是等腰三角形的顶角时,另外两个内角是底角.
则两个底角的度数都是
(180°-40°)=70°,
所以另外两个内角的度数分别为70°,70°.
②当已知角是等腰三角形的底角时,另外两个内角一个是底角,
一个是顶角.
则底角的度数都是40°,顶角度数为(180°-40°-40°)=100°,
综上所述,另外两个内角为70°,70°或40°,100°.
拓展提升
1
(3)已知一个等腰三角形的两条边的长度比是3:2,且有一条边的长为12厘米,这个等腰三角形的周长最大是多少?
分析:等腰三角形的两条边的长度比是3:2,有一条边的长为12厘米,所以另外一条边是8厘米或者18厘米.此时已经有两种情况需要讨论:
①12厘米,8厘米
②12厘米,18厘米
还需注意的是等腰三角形也要分情况讨论,哪段为腰,哪段为底边.
拓展提升
1
解:因为等腰三角形一条边长为12厘米,并且两条边的长度比为3:2,
所以和它不相等的另外一条边的长为8厘米或18厘米.
①当腰长为8厘米,底边长为12厘米时,周长为8+8+12=28(厘米);
②当腰长为12厘米,底边长为8厘米时,周长为8+12+12=32(厘米);
③当腰长为12厘米,底边长为18厘米时,周长为18+12+12=42(厘米);
④当腰长为18厘米,底边长为12厘米时,周长为18+18+12=48(厘米).
因为28<32<42<48,所以这个等腰三角形的周长最大为48厘米.
(3)已知一个等腰三角形的两条边的长度比是3:2,且有一条边的长为12厘米,这个等腰三角形的周长最大是多少?
13.3.1 等边三角形
等腰三角形
知识回顾
定义:两边相等的三角形叫做等腰三角形.
如图,△ABC为等腰三角形,其中AB=AC,则AB,AC为腰,BC为底边,两腰的夹角为顶角,腰与底边的夹角为底角.
A
B
C
腰
腰
底边
顶
角
底角
学习目标
1、了解等腰三角形的性质,体会等腰三角形“三线合一”的意义.
2、探索并掌握等腰三角形的性质,并用以解决实际问题.
课堂导入
如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点.
剪刀剪过的两条边是相等的,即△ABC中AB=AC,所以△ABC是等腰三角形.
A
C
B
D
新知探究
把剪出的等腰三角形ABC沿着折痕对折,找出其中重合的线段和角.
由得出的重合的线段和角,你能发现等腰三角形的性质吗?试试说出你的猜想.
重合的线段:AB和AC,BD和CD;
重合的角:∠BAD=∠CAD,
∠B=∠C,
∠ADB=∠ADC.
A
C
B
D
新知探究
猜想:等腰三角形的两个底角相等,折痕AD为∠BAC的角平分线,为底边BC的中线,为底边BC的高.
重合的线段:AB和AC,BD和CD;
重合的角:∠BAD=∠CAD,
∠B=∠C,
∠ADB=∠ADC.
在一张白纸上任意画一个等腰三角形,把它剪下来,请试试折叠,此时猜想仍然成立吗?
A
C
B
D
应用“等边对等角”的前提条件是在同一个三角形中,不在同一个三角形中不能使用.
新知探究
等腰三角形的性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
知识点1
几何语言:如图,在△ABC中,
∵AB=AC,
∴∠B=∠C.
A
B
C
新知探究
知识点1
(1)“等边对等角”是证明三角形中两个角相等的常用方法,这种方法比利用三角形全等证明两个角相等更方便.
(2)在等腰三角形中,依据三角形内角和等于180°,可以由顶角求底角,也可以由底角求顶角,且注意:如果已知条件中未说明是顶角还是底角时,要考虑所有可能的情况并分类讨论.
新知探究
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).
知识点2
几何语言:如图,在△ABC中,
①∵AB=AC,AD平分∠BAC,
∴AD⊥BC,BD=CD.
②∵AB=AC,AD⊥BC,
∴AD平分∠BAC
,BD=CD.
③∵AB=AC,BD=CD,
∴AD平分∠BAC,AD⊥BC.
你能不能证明①②③的结论?
B
C
D
A
新知探究
知识点2
如图,在△ABC中,AB=AC,AD平分∠BAC,
求证:AD⊥BC,∠ADB=∠ADC
.
证明:∵AD平分∠BAC,
∴∠BAD=∠CAD.
在△ABD和△ACD中,
AB=AC,
∠BAD=∠CAD,
AD=AD,
∴△ABD≌△ACD(SAS).
∴∠BAD=∠CAD,∠ADB=∠ADC.
∵
∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC.
B
C
D
A
新知探究
知识点2
如图,在△ABC中,AB=AC,AD是底边BC的中线,
求证:AD⊥BC,AD平分∠BAC.
证明:∵AD是底边BC的中线,
∴BD=CD.
在△ABD和△ACD中,
AB=AC,
BD=CD,
AD=AD,
∴△ABD≌△ACD(SSS).
∴BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
∴AD平分∠BAC.
∵
∠ADB+∠ADC=180°,
∴∠ADB=∠ADC=90°,即AD⊥BC.
B
C
D
A
新知探究
知识点2
如图,在△ABC中,AB=AC,AD是底边BC的高,
求证:∠BAD=∠CAD
,BD=CD.
证明:∵AD是底边BC的高,
∴∠ADB=∠ADC=90°.
在Rt△ABD和Rt△ACD中,AB=AC,
AD=AD,
∴Rt△ABD≌Rt△ACD(HL).
∴BD=CD,∠BAD=∠CAD
.
B
C
D
A
新知探究
知识点2
(1)“三线合一”的性质应用非常广泛,可以用来证明角相等、线段相等或线段垂直.
(2)等腰三角形是轴对称图形,对称轴为顶角平分线(或底边上的高或底边上的中线)所在的直线.
应用“三线合一”的前提条件是等腰三角形,且必须是底边上的中线、底边上的高和顶角的平分线才能互相重合.
新知探究
知识点2
等腰三角形的其他性质:
(1)等腰三角形两腰上的中线相等,两腰上的高相等,两底角的平分线也相等.
(2)等腰三角形底边上的任意一点到两腰的距离之和等于一腰上的高.
(3)等腰三角形底边上的高(或底边上的中线或顶角平分线)上任意一点到两腰的距离相等.
解:∵AB=AC,∠BAC=90°
,
∴∠B=∠C=45°.
∵AB=AC,AD是底边BC上的高,
∴AD是∠BAC的平分线,则∠BAD=∠DAC=45°.
∴AD是底边BC上的中线,则BD=CD.
跟踪训练
新知探究
如图,△ABC是等腰三角形(AB=AC,∠BAC=90°),AD是底边BC上的高,请写出∠B,∠C,∠BAD,∠DAC的度数,并说明BD=CD.
A
B
C
┐
┐
跟踪训练
新知探究
如图,在△ABC中,已知AB=AC,D为BC的中点,∠BAD=35°,则∠C的度数为(
)
A.35°
B.45°
C.55°
D.60°
解:∵AB=AC,D为BC的中点,
∴∠B=∠C,AD⊥BC.
∵∠B=90°-∠BAD=55°,
∴∠C=55°.
C
如图,在△ABC中,AB=AC,D为BC上一点,且DA=DC,BD=BA,则∠B的大小为(
)
A.40°
B.36°
C.80°
D.25°
随堂练习
1
解:∵AB=AC,
∴∠C=∠B.
∵BD=BA,DA=DC,
∴∠BAD=∠BDA=2∠C=2∠B.
设∠C=∠B=x,则∠BAD=∠BDA=2x.
∵∠B+∠BAD+∠BDA=180°,
∴x=36°.
∴∠B=36°.
B
如图,AB//CD,AD=CD,∠1=65°,则∠2的度数为(
)
A.50°
B.60°
C.65°
D.70°
随堂练习
2
解:∵AB//CD,∠1=65°,
∴∠ACD=∠1=65°.
∵AD=CD,
∴∠DCA=∠DAC=65°.
∴∠2的度数为:180°-
65°-65°=50°.
A
随堂练习
3
如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
D
解:∵∠BAD=26°,AB=AD,
∴∠B=∠ADB=
(180°-26°)=77°.
∵AD=CD,
∴∠C=∠DAC.
∵∠ADB=77°,∠ADB=∠C+∠DAC,
∴∠C的度数为
∠ADB=38.5°.
B
A
C
课堂小结
等腰
三角形
定义
性质
有两边相等的三角形
等边对等角
三线合一
拓展提升
1
(1)已知一个等腰三角形的一个内角是130°,它的另外两个内角是多少度?
(2)已知一个等腰三角形的一个内角是40°,它的另外两个内角是多少度?
(3)已知一个等腰三角形的两条边的长度比是3:2,且有一条边的长为12厘米,这个等腰三角形的周长最大是多少?
拓展提升
1
(1)已知一个等腰三角形的一个内角是130°,它的另外两个内角是多少度?
解:因为等腰三角形的两个底角相等,
所以这个已知的角只能是顶角,
则两个底角的度数都是
(180°-130°)=25°,
所以另外两个内角的度数分别为25°,25°.
拓展提升
1
(2)已知一个等腰三角形的一个内角是40°,它的另外两个内角是多少度?
解:①当已知角是等腰三角形的顶角时,另外两个内角是底角.
则两个底角的度数都是
(180°-40°)=70°,
所以另外两个内角的度数分别为70°,70°.
②当已知角是等腰三角形的底角时,另外两个内角一个是底角,
一个是顶角.
则底角的度数都是40°,顶角度数为(180°-40°-40°)=100°,
综上所述,另外两个内角为70°,70°或40°,100°.
拓展提升
1
(3)已知一个等腰三角形的两条边的长度比是3:2,且有一条边的长为12厘米,这个等腰三角形的周长最大是多少?
分析:等腰三角形的两条边的长度比是3:2,有一条边的长为12厘米,所以另外一条边是8厘米或者18厘米.此时已经有两种情况需要讨论:
①12厘米,8厘米
②12厘米,18厘米
还需注意的是等腰三角形也要分情况讨论,哪段为腰,哪段为底边.
拓展提升
1
解:因为等腰三角形一条边长为12厘米,并且两条边的长度比为3:2,
所以和它不相等的另外一条边的长为8厘米或18厘米.
①当腰长为8厘米,底边长为12厘米时,周长为8+8+12=28(厘米);
②当腰长为12厘米,底边长为8厘米时,周长为8+12+12=32(厘米);
③当腰长为12厘米,底边长为18厘米时,周长为18+12+12=42(厘米);
④当腰长为18厘米,底边长为12厘米时,周长为18+18+12=48(厘米).
因为28<32<42<48,所以这个等腰三角形的周长最大为48厘米.
(3)已知一个等腰三角形的两条边的长度比是3:2,且有一条边的长为12厘米,这个等腰三角形的周长最大是多少?
