人教版八年级数学上册13.3等腰三角形课时4课件(20张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.3等腰三角形课时4课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 129.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 09:38:10 | ||
图片预览







文档简介
(共20张PPT)
13.3.4 等边三角形
等腰三角形
知识回顾
等边三角形的性质:
1、等边三角形的三条边相等,三个角相等,都为60°;
2、等边三角形满足等边对等角;
3、等边三角形各边上的高、中线和所对角的平分线相互重合;
4、等边三角形是轴对称图形,且有三条对称轴.
学习目标
1、了解等边三角形的判定方法.
2、探索并掌握等边三角形判定的过程,并用以解决实际问题.
课堂导入
思考1:等腰三角形的判定?
如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边).
所以这个三角形是等腰三角形.
那么三角形的三个内角都相等是否可以判定它是等边三角形,你能证明这个结论吗?
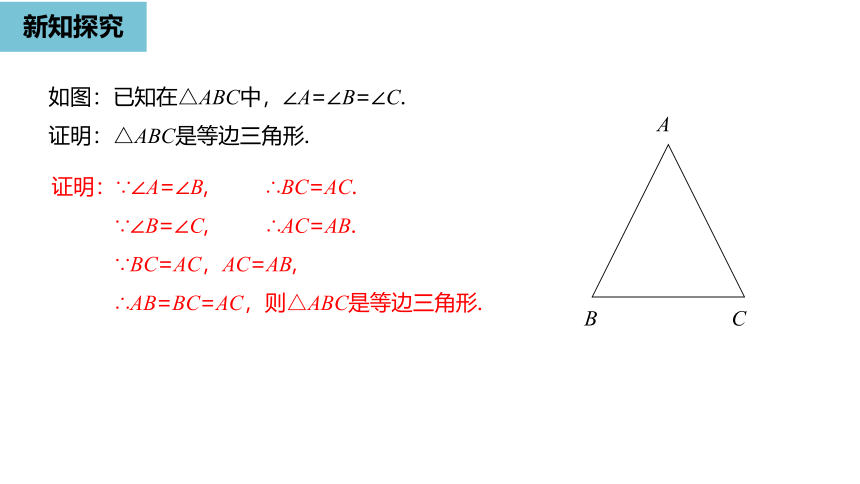
如图:已知在△ABC中,∠A=∠B=∠C.
证明:△ABC是等边三角形.
证明:∵∠A=∠B,
∴BC=AC.
∵∠B=∠C,
∴AC=AB.
∵BC=AC,AC=AB,
∴AB=BC=AC,则△ABC是等边三角形.
A
B
C
新知探究
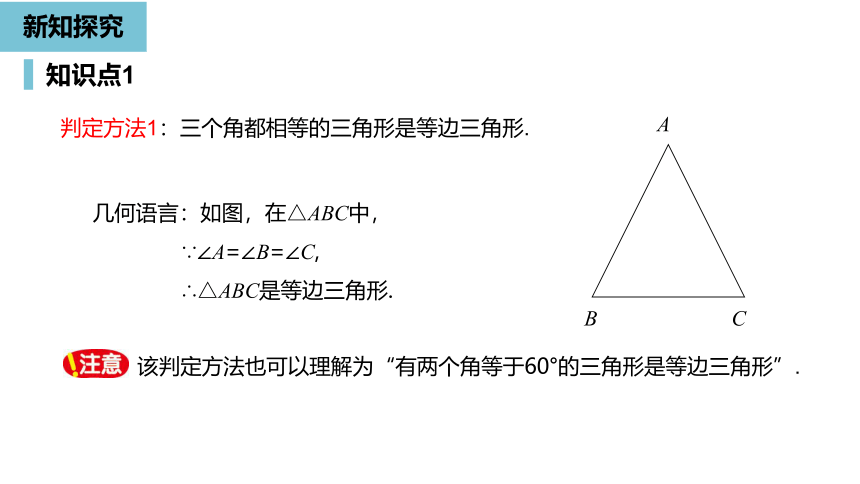
判定方法1:三个角都相等的三角形是等边三角形.
新知探究
知识点1
几何语言:如图,在△ABC中,
∵∠A=∠B=∠C,
∴△ABC是等边三角形.
该判定方法也可以理解为“有两个角等于60°的三角形是等边三角形”.
A
B
C
新知探究
思考2:等腰三角形有两边相等,能否添加什么条件使得等腰三角形成为等边三角形呢?
结论:1、等腰三角形的腰和底边相等;
2、有一个角是60°的等腰三角形;
结论1其实就是三边相等的三角形,也即是等边三角形,那你能证明结论2吗?
如图:已知在△ABC中,AB=AC,∠A=60°.
证明:△ABC是等边三角形.
证明:∵AB=AC,
∴∠C=∠B
.
∵∠A=60°,
∴∠B+∠C=180°-∠A=120°
.
∴∠A=∠B=∠C=60°.
∴△ABC是等边三角形.
A
B
C
新知探究
证明:∵AB=AC,∠B=60°
,
∴∠C=∠B=60°
.
∴∠A=180°-(∠B+∠C)=60°
,
∴∠A=∠B=∠C.
∴△ABC是等边三角形.
新知探究
A
B
C
如图:已知在△ABC中,AB=AC,∠B=60°.
证明:△ABC是等边三角形.
判定方法2:有一个角是60°的等腰三角形是等边三角形.
新知探究
知识点2
(1)在等腰三角形中,只要有一个角是60°
,无论这个角是顶角还是底角,这个三角形就是等边三角形;
(2)等边三角形的判定方法的选用:若已知三边关系,一般选用定义判定;若已知三角关系,一般选用判定方法1;若已知该三角形是等腰三角形,一般选用判定方法2.
新知探究
例题:如图,△ABC是等边三角形,DE//BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C.
∴∠A=∠ADE=∠AED.
∴△ADE是等边三角形.
A
B
C
D
E
跟踪训练
新知探究
如图,等边三角形ABC中,AD是BC边上的高,∠BDE=∠CDF=60°,图中有哪些与BD相等的线段?
解:图中与BD相等的线段有CD,CF,BE,DE,FD,AF,AE.
容易证明△BDE,△CDF是等边三角形,
容易漏掉证明AE,AF与BD相等.
A
B
C
E
F
D
跟踪训练
新知探究
∵△ABC是等边三角形,AD是BC边上的高,∠BDE=∠CDF=60°
∴AD为BC的中线,AD为∠BAC的平分线.
∴∠BAC=∠B=∠C=60°,BD=CD,∠BAD=∠CAD=30°.
∵∠B=∠BDE=60°,
∴△BDE是等边三角形,∴BD=BE=DE.
同理,△CDF是等边三角形,∴CD=CF=DF.
∵AD是BC上的高,
∴∠ADB=90°.
∵∠BDE=60°,
∴∠ADE=∠ADB-∠BDE=30°.
∵∠ADE=∠BAD=30°,
∴AE=DE.
同理:AF=DF,
∴BD=CD=CF=BE=DE=FD=AF=AE.
A
B
C
E
F
D
随堂练习
1
已知等腰三角形的一边长为8,一个内角为60°,则它的周长为多少?
解:∵等腰三角形的一个内角为60°,
∴该等腰三角形是等边三角形,
∵该三角形的一边长为8,
∴它的周长为8+8+8=24.
下列条件中不能得到等边三角形的是(
)
A.有一个角是60°的等腰三角形
B.三边相等的三角形
C.有两个内角是60°的三角形
D.有两个外角相等的等腰三角形
随堂练习
2
D
D选项中若是顶角和底角的外角相等,则说明顶角和底角相等,此时等腰三角形的三个内角相等,可以得到等边三角形;
若是两个底角的外角相等,则不能得到等边三角形.
如图,AC和BD相交于点O,若OA=OB,∠A=60?,且AB//CD.
求证:△OCD是等边三角形.
随堂练习
3
证明:∵∠A=60°,OA=OB,
∴∠B=∠A=60°.
∵AB//CD,
∴∠C=∠A=60°,∠D=∠B=60°.
∴∠COD=60°.
∴∠C=∠D=∠COD=60°,
∴△OCD是等边三角形.
A
B
C
D
O
课堂小结
等边三角形的判定
性质
判定方法2
三边相等的三角形是
等边三角形.
有一个角是60°的等腰三角形是等边三角形.
判定方法1
三个角都相等的三角形是
等边三角形.
拓展提升
1
如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
(1)若∠B=60°,求∠C的度数;
(2)求证:AD是∠EAC的平分线.
分析:(1)△ABD中∠BDA=∠BAD,∠B=60°,则
△ABD是等边三角形.由CD=AB,∠BDA=60°,可得
∠C=30°.
(2)证明AD是∠EAC的平分线也即是证明∠EAD=∠CAD,一般选用三角形全等或者等边对等角.
拓展提升
1
解:(1)∵∠BDA=∠BAD,∠B=60°,
∴∠BDA=∠BAD=
(180°-60°)=60°.
∴△ABD是等边三角形,AB=AD.
∵CD=AB,
∴CD=AD,∠DAC=∠C.
∵∠BDA=∠DAC+∠C=60°,
∴∠C=30°.
如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
(1)若∠B=60°,求∠C的度数;
(2)求证:AD是∠EAC的平分线.
拓展提升
1
(2)延长AE到点M,使得EM=AE,连接DM.
∵AE是△ABD的中线,
∴BE=DE.
在△ABE和△MDE中,
EA=EM,
∠AEB=∠MED,
BE=DE,∴△ABE≌△MDE,∴AB=DM,∠ABE=∠MDE.
∵∠ADC=∠ABE+∠BAD,∠ADM=∠MDE+∠ABD,
∴∠ADC=∠ADM.
∵CD=AB,AB=DM,
∴CD=DM.
在△MAD和△CAD中,DM=CD,
∠ADM=∠ADC,
AD=AD,
∴△MAD≌△CAD,∠MAD=∠CAD.
∴AD是∠EAC的平分线.
M
13.3.4 等边三角形
等腰三角形
知识回顾
等边三角形的性质:
1、等边三角形的三条边相等,三个角相等,都为60°;
2、等边三角形满足等边对等角;
3、等边三角形各边上的高、中线和所对角的平分线相互重合;
4、等边三角形是轴对称图形,且有三条对称轴.
学习目标
1、了解等边三角形的判定方法.
2、探索并掌握等边三角形判定的过程,并用以解决实际问题.
课堂导入
思考1:等腰三角形的判定?
如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边).
所以这个三角形是等腰三角形.
那么三角形的三个内角都相等是否可以判定它是等边三角形,你能证明这个结论吗?
如图:已知在△ABC中,∠A=∠B=∠C.
证明:△ABC是等边三角形.
证明:∵∠A=∠B,
∴BC=AC.
∵∠B=∠C,
∴AC=AB.
∵BC=AC,AC=AB,
∴AB=BC=AC,则△ABC是等边三角形.
A
B
C
新知探究
判定方法1:三个角都相等的三角形是等边三角形.
新知探究
知识点1
几何语言:如图,在△ABC中,
∵∠A=∠B=∠C,
∴△ABC是等边三角形.
该判定方法也可以理解为“有两个角等于60°的三角形是等边三角形”.
A
B
C
新知探究
思考2:等腰三角形有两边相等,能否添加什么条件使得等腰三角形成为等边三角形呢?
结论:1、等腰三角形的腰和底边相等;
2、有一个角是60°的等腰三角形;
结论1其实就是三边相等的三角形,也即是等边三角形,那你能证明结论2吗?
如图:已知在△ABC中,AB=AC,∠A=60°.
证明:△ABC是等边三角形.
证明:∵AB=AC,
∴∠C=∠B
.
∵∠A=60°,
∴∠B+∠C=180°-∠A=120°
.
∴∠A=∠B=∠C=60°.
∴△ABC是等边三角形.
A
B
C
新知探究
证明:∵AB=AC,∠B=60°
,
∴∠C=∠B=60°
.
∴∠A=180°-(∠B+∠C)=60°
,
∴∠A=∠B=∠C.
∴△ABC是等边三角形.
新知探究
A
B
C
如图:已知在△ABC中,AB=AC,∠B=60°.
证明:△ABC是等边三角形.
判定方法2:有一个角是60°的等腰三角形是等边三角形.
新知探究
知识点2
(1)在等腰三角形中,只要有一个角是60°
,无论这个角是顶角还是底角,这个三角形就是等边三角形;
(2)等边三角形的判定方法的选用:若已知三边关系,一般选用定义判定;若已知三角关系,一般选用判定方法1;若已知该三角形是等腰三角形,一般选用判定方法2.
新知探究
例题:如图,△ABC是等边三角形,DE//BC,分别交AB,AC于点D,E.
求证:△ADE是等边三角形.
证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C.
∵DE//BC,
∴∠ADE=∠B,∠AED=∠C.
∴∠A=∠ADE=∠AED.
∴△ADE是等边三角形.
A
B
C
D
E
跟踪训练
新知探究
如图,等边三角形ABC中,AD是BC边上的高,∠BDE=∠CDF=60°,图中有哪些与BD相等的线段?
解:图中与BD相等的线段有CD,CF,BE,DE,FD,AF,AE.
容易证明△BDE,△CDF是等边三角形,
容易漏掉证明AE,AF与BD相等.
A
B
C
E
F
D
跟踪训练
新知探究
∵△ABC是等边三角形,AD是BC边上的高,∠BDE=∠CDF=60°
∴AD为BC的中线,AD为∠BAC的平分线.
∴∠BAC=∠B=∠C=60°,BD=CD,∠BAD=∠CAD=30°.
∵∠B=∠BDE=60°,
∴△BDE是等边三角形,∴BD=BE=DE.
同理,△CDF是等边三角形,∴CD=CF=DF.
∵AD是BC上的高,
∴∠ADB=90°.
∵∠BDE=60°,
∴∠ADE=∠ADB-∠BDE=30°.
∵∠ADE=∠BAD=30°,
∴AE=DE.
同理:AF=DF,
∴BD=CD=CF=BE=DE=FD=AF=AE.
A
B
C
E
F
D
随堂练习
1
已知等腰三角形的一边长为8,一个内角为60°,则它的周长为多少?
解:∵等腰三角形的一个内角为60°,
∴该等腰三角形是等边三角形,
∵该三角形的一边长为8,
∴它的周长为8+8+8=24.
下列条件中不能得到等边三角形的是(
)
A.有一个角是60°的等腰三角形
B.三边相等的三角形
C.有两个内角是60°的三角形
D.有两个外角相等的等腰三角形
随堂练习
2
D
D选项中若是顶角和底角的外角相等,则说明顶角和底角相等,此时等腰三角形的三个内角相等,可以得到等边三角形;
若是两个底角的外角相等,则不能得到等边三角形.
如图,AC和BD相交于点O,若OA=OB,∠A=60?,且AB//CD.
求证:△OCD是等边三角形.
随堂练习
3
证明:∵∠A=60°,OA=OB,
∴∠B=∠A=60°.
∵AB//CD,
∴∠C=∠A=60°,∠D=∠B=60°.
∴∠COD=60°.
∴∠C=∠D=∠COD=60°,
∴△OCD是等边三角形.
A
B
C
D
O
课堂小结
等边三角形的判定
性质
判定方法2
三边相等的三角形是
等边三角形.
有一个角是60°的等腰三角形是等边三角形.
判定方法1
三个角都相等的三角形是
等边三角形.
拓展提升
1
如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
(1)若∠B=60°,求∠C的度数;
(2)求证:AD是∠EAC的平分线.
分析:(1)△ABD中∠BDA=∠BAD,∠B=60°,则
△ABD是等边三角形.由CD=AB,∠BDA=60°,可得
∠C=30°.
(2)证明AD是∠EAC的平分线也即是证明∠EAD=∠CAD,一般选用三角形全等或者等边对等角.
拓展提升
1
解:(1)∵∠BDA=∠BAD,∠B=60°,
∴∠BDA=∠BAD=
(180°-60°)=60°.
∴△ABD是等边三角形,AB=AD.
∵CD=AB,
∴CD=AD,∠DAC=∠C.
∵∠BDA=∠DAC+∠C=60°,
∴∠C=30°.
如图,已知D是△ABC的边BC上的一点,CD=AB,∠BDA=∠BAD,AE是△ABD的中线.
(1)若∠B=60°,求∠C的度数;
(2)求证:AD是∠EAC的平分线.
拓展提升
1
(2)延长AE到点M,使得EM=AE,连接DM.
∵AE是△ABD的中线,
∴BE=DE.
在△ABE和△MDE中,
EA=EM,
∠AEB=∠MED,
BE=DE,∴△ABE≌△MDE,∴AB=DM,∠ABE=∠MDE.
∵∠ADC=∠ABE+∠BAD,∠ADM=∠MDE+∠ABD,
∴∠ADC=∠ADM.
∵CD=AB,AB=DM,
∴CD=DM.
在△MAD和△CAD中,DM=CD,
∠ADM=∠ADC,
AD=AD,
∴△MAD≌△CAD,∠MAD=∠CAD.
∴AD是∠EAC的平分线.
M
