人教版八年级数学上册13.3等腰三角形课时3课件(23张PPT)
文档属性
| 名称 | 人教版八年级数学上册13.3等腰三角形课时3课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 163.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 09:39:17 | ||
图片预览






文档简介
(共23张PPT)
13.3.3 等边三角形
等腰三角形
知识回顾
等腰三角形的性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).
等腰三角形的概念:两边相等的三角形是等腰三角形.
学习目标
1、理解等腰三角形的性质,体会等腰三角形性质和等边三角形性质的联系.
2、探索并掌握等边三角形性质的过程,并用以解决实际问题.
课堂导入
思考1:如果把等腰三角形的性质用于等边三角形,你能得到什么结论?
结论:等边三角形的三条边都相等,是一种特殊的等腰三角形.所以等边三角形具有等腰三角形的所有性质.
课堂导入
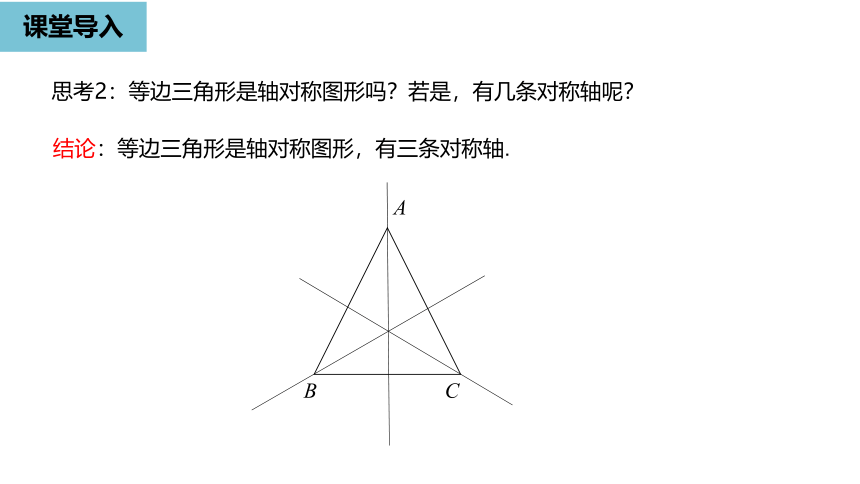
思考2:等边三角形是轴对称图形吗?若是,有几条对称轴呢?
结论:等边三角形是轴对称图形,有三条对称轴.
A
B
C
课堂导入
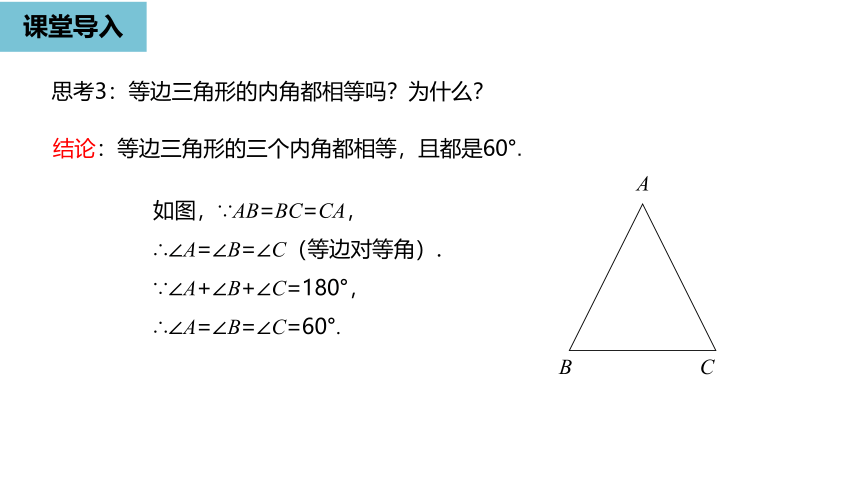
思考3:等边三角形的内角都相等吗?为什么?
结论:等边三角形的三个内角都相等,且都是60°.
A
B
C
如图,∵AB=BC=CA,
∴∠A=∠B=∠C(等边对等角).
∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°.
新知探究
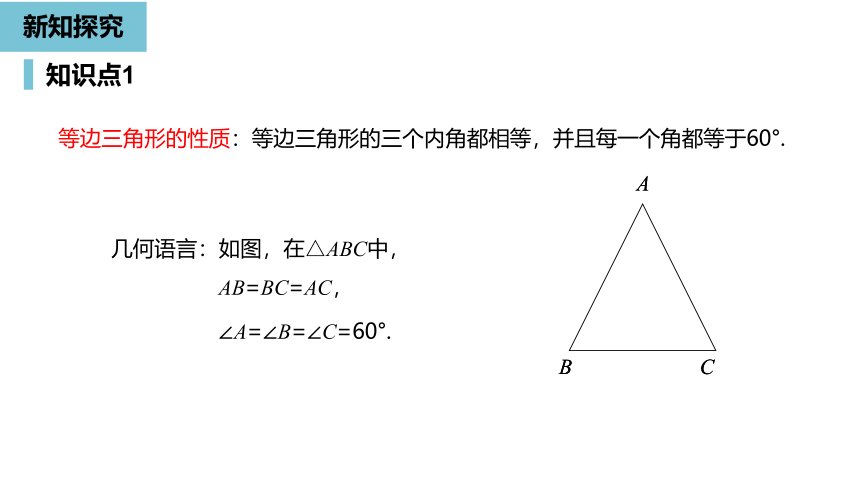
等边三角形的性质:等边三角形的三个内角都相等,并且每一个角都等于60°.
知识点1
几何语言:如图,在△ABC中,
AB=BC=AC,
∠A=∠B=∠C=60°.
A
B
C
A
B
C
(1)等边三角形是特殊的等腰三角形,它具有等腰三角形的所有性质.
(2)等边三角形每条边上的中线、高和所对角的平分线相互重合,即“三线合一”;每条边上的中线和高的长度相等,且所在的直线都是等边三角形的对称轴.
新知探究
知识点1
新知探究
例1:如图,已知△ABC,△BDE都是等边三角形,求证:AE=CD.
证明:∵△ABC,△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°.
∵在△ABE和△CBD中,AB=CB,
∠ABE=∠CBD,
BE=BD,
∴△ABE≌△CBD(SAS).
∴AE=CD.
A
B
D
C
E
跟踪训练
新知探究
如图,等边三角形ABC的边长为3,点D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
分析:利用等边三角形的性质、等腰三角形的性质及三角形内角和定理的推论,求出∠CDE=∠E,从而将求CE的长转化为求CD的长.
A
B
C
D
E
跟踪训练
新知探究
如图,等边三角形ABC的边长为3,点D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
E
解:∵△ABC是等边三角形,D是AC的中点,
∴∠ABC=∠ACB=60°,BD为∠ABC的平分线,
∴∠DBE=
∠ABC=30°.
∵DE=DB,
∴∠E=∠DBE=30°.
∵∠ACB=∠CDE+∠E,
∴∠CDE=∠ACB-∠E=30°.
∴∠CDE=∠E.
∴CD=CE.
∵等边三角形ABC的边长为3,点D是AC的中点,
∴CE=CD=
.
A
B
C
D
E
随堂练习
1
如图,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=(
)
A.15°
B.20°
C.25°
D.30°
解:∵△ABC是等边三角形,
∴∠ACB=60°.
∵CG=CD,
∴∠CGD
=∠CDG.
∴∠ACB
=∠CGD+∠CDG=2∠CDG.
同理可得∠CDG=2∠E,
∴∠ACB
=4∠E=60°.
∴∠E=15°.
A
如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于(
)
A.15°
B.30°
C.45°
D.60°
随堂练习
2
分析:△ABC是等边三角形,所以三个内角均为60°.通过证明△EDB≌△EDC,可求出∠ECB的度数,∠ACE=∠ACB-∠ECD即可求解.
随堂练习
2
解:∵△ABC是等边三角形,AD⊥BC,
∴BD=CD,∠EDB=∠EDC,∠ACB=60°.
∵在△EDB和△EDC中,
ED=ED,
∠EDB=∠EDC,
BD=CD,
∴△EDB≌△EDC(SAS).
∴∠ACE=∠ACB-∠ECD=60°-45°=15°.
A
如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于(
)
A.15°
B.30°
C.45°
D.60°
如图,在等边三角形ABC中,D,E分别是AB,AC上的点,且AD=CE,则∠BCD+∠CBE的大小是多少?
随堂练习
3
分析:△ABC是等边三角形,所以三个内角均为60°,三边相等.通过证明△ADC≌△CEB,可求出∠CBE=∠ACD,则∠BCD+∠CBE=∠BCD+∠ACD=∠ACB.
E
D
B
C
A
随堂练习
3
解:∵△ABC是等边三角形,
∴∠ACB=∠A=∠ABC=60°,且AB=BC=AC.
∵在△ADC和△CEB中,
AC=CB,
∠A=∠BCE,
AD=CE,
∴△ADC≌△CEB(SAS),∠CBE=∠ACD.
∴∠BCD+∠CBE=∠BCD+∠ACD=∠ACB=60°.
E
D
B
C
A
如图,在等边三角形ABC中,D,E分别是AB,AC上的点,且AD=CE,则∠BCD+∠CBE的大小是多少?
正三角形ABC的两条角平分线BD和CE相交于点F,则∠BFC的度数是多少?
随堂练习
4
解:∵△ABC是正三角形,
∴∠ABC=∠ACB=60°.
∵BD和CE是正三角形ABC的角平分线,
∴∠ECB=30°,∠DBC=30°.
在△BFC中,∠BFC=180°-∠ECB-∠DBC
=180°-30°-30°
=120°.
A
B
C
D
E
F
课堂小结
等边
三角形
定义
性质
三边都相等的三角形.
三边相等,三个角相等,具有等腰三角形的一切性质.
拓展提升
1
如图,△ABC是等边三角形,△ADE是等腰三角形,AD=AE,∠DAE=80°,当DE⊥AC时,求∠BAD和∠EDC的度数.
分析:首先利用等腰三角形的性质得出
∠ADE=∠E=50°,∠DAF=∠EAF=40°,进而利用等边三角形各内角度数求出∠BAD即可,再利用三角形外角性质得出答案.
A
B
C
F
E
D
拓展提升
1
解:∵DE⊥AC,
∴∠DFA=∠EFA=90°.
∵AD=AE,∠DAE=80°,
∴∠ADE=∠E=50°.
∴∠DAF=∠EAF=40°.
∵△ABC是等边三角形,
∴∠BAC=60°.
∴∠BAD=∠BAC-∠DAF=20°.
∵∠B+∠BAD=∠ADC=∠ADE+∠EDC,
∴∠EDC=60°+20°-50°=30°.
如图,△ABC是等边三角形,△ADE是等腰三角形,AD=AE,∠DAE=80°,当DE⊥AC时,求∠BAD和∠EDC的度数.
A
B
C
F
E
D
拓展提升
2
如图,△ABC是边长为1的等边三角形,BD=CD,∠BDC=120°,点E,F分别在AB,AC上,且∠EDF=60°.求△AEF的周长.
分析:由∠BDC=120°和∠EDF=60°,得到
∠BDE+∠CDF=60°.想把这两个三角形拼在一起构造全等三角形,即延长AC至点P,使得CP=BE,证明△DEF≌△DPF,得到EF=PF,从而把△AEF的周长转化为△ABC的边长表示.
A
B
C
F
E
D
拓展提升
2
解:延长AC至点P,使得CP=BE,连接PD
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°.
∴∠EBD=∠DCF=90°.
∴∠DCP=∠DBE=90°.
在△BDE和△CDP中
,
BD=CD
∠DBE=∠DCP
BE=CP
∴△BDE≌△CDP.
C
P
A
B
F
E
如图,△ABC是边长为1的等边三角形,BD=CD,∠BDC=120°,点E,F分别在AB,AC上,且∠EDF=60°.求△AEF的周长.
D
拓展提升
2
∵△BDE≌△CDP,
∴DE=DP,∠BDE=∠CDP.
∵∠BDC=120°,
∠EDF=60°,
∴∠BDE+∠CDF=60°,∠CDP+∠CDF=60°.
∴∠EDF=∠PDF=60°.
在△DEF和△DPF中,
DE=DP,
∠EDF=∠PDF,
DF=DF,
∴△DEF≌△DPF.
∴EF=FP,EF=FC+BE.
∴△AEF的周长=AE+EF+AF=AE+FC+BE+AF=AB+AC=2.
C
A
B
F
E
D
P
13.3.3 等边三角形
等腰三角形
知识回顾
等腰三角形的性质1:等腰三角形的两个底角相等(简写成“等边对等角”).
等腰三角形的性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简写成“三线合一”).
等腰三角形的概念:两边相等的三角形是等腰三角形.
学习目标
1、理解等腰三角形的性质,体会等腰三角形性质和等边三角形性质的联系.
2、探索并掌握等边三角形性质的过程,并用以解决实际问题.
课堂导入
思考1:如果把等腰三角形的性质用于等边三角形,你能得到什么结论?
结论:等边三角形的三条边都相等,是一种特殊的等腰三角形.所以等边三角形具有等腰三角形的所有性质.
课堂导入
思考2:等边三角形是轴对称图形吗?若是,有几条对称轴呢?
结论:等边三角形是轴对称图形,有三条对称轴.
A
B
C
课堂导入
思考3:等边三角形的内角都相等吗?为什么?
结论:等边三角形的三个内角都相等,且都是60°.
A
B
C
如图,∵AB=BC=CA,
∴∠A=∠B=∠C(等边对等角).
∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°.
新知探究
等边三角形的性质:等边三角形的三个内角都相等,并且每一个角都等于60°.
知识点1
几何语言:如图,在△ABC中,
AB=BC=AC,
∠A=∠B=∠C=60°.
A
B
C
A
B
C
(1)等边三角形是特殊的等腰三角形,它具有等腰三角形的所有性质.
(2)等边三角形每条边上的中线、高和所对角的平分线相互重合,即“三线合一”;每条边上的中线和高的长度相等,且所在的直线都是等边三角形的对称轴.
新知探究
知识点1
新知探究
例1:如图,已知△ABC,△BDE都是等边三角形,求证:AE=CD.
证明:∵△ABC,△BDE都是等边三角形,
∴AB=BC,BE=BD,∠ABC=∠DBE=60°.
∵在△ABE和△CBD中,AB=CB,
∠ABE=∠CBD,
BE=BD,
∴△ABE≌△CBD(SAS).
∴AE=CD.
A
B
D
C
E
跟踪训练
新知探究
如图,等边三角形ABC的边长为3,点D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
分析:利用等边三角形的性质、等腰三角形的性质及三角形内角和定理的推论,求出∠CDE=∠E,从而将求CE的长转化为求CD的长.
A
B
C
D
E
跟踪训练
新知探究
如图,等边三角形ABC的边长为3,点D是AC的中点,点E在BC的延长线上,若DE=DB,求CE的长.
E
解:∵△ABC是等边三角形,D是AC的中点,
∴∠ABC=∠ACB=60°,BD为∠ABC的平分线,
∴∠DBE=
∠ABC=30°.
∵DE=DB,
∴∠E=∠DBE=30°.
∵∠ACB=∠CDE+∠E,
∴∠CDE=∠ACB-∠E=30°.
∴∠CDE=∠E.
∴CD=CE.
∵等边三角形ABC的边长为3,点D是AC的中点,
∴CE=CD=
.
A
B
C
D
E
随堂练习
1
如图,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=(
)
A.15°
B.20°
C.25°
D.30°
解:∵△ABC是等边三角形,
∴∠ACB=60°.
∵CG=CD,
∴∠CGD
=∠CDG.
∴∠ACB
=∠CGD+∠CDG=2∠CDG.
同理可得∠CDG=2∠E,
∴∠ACB
=4∠E=60°.
∴∠E=15°.
A
如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于(
)
A.15°
B.30°
C.45°
D.60°
随堂练习
2
分析:△ABC是等边三角形,所以三个内角均为60°.通过证明△EDB≌△EDC,可求出∠ECB的度数,∠ACE=∠ACB-∠ECD即可求解.
随堂练习
2
解:∵△ABC是等边三角形,AD⊥BC,
∴BD=CD,∠EDB=∠EDC,∠ACB=60°.
∵在△EDB和△EDC中,
ED=ED,
∠EDB=∠EDC,
BD=CD,
∴△EDB≌△EDC(SAS).
∴∠ACE=∠ACB-∠ECD=60°-45°=15°.
A
如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于(
)
A.15°
B.30°
C.45°
D.60°
如图,在等边三角形ABC中,D,E分别是AB,AC上的点,且AD=CE,则∠BCD+∠CBE的大小是多少?
随堂练习
3
分析:△ABC是等边三角形,所以三个内角均为60°,三边相等.通过证明△ADC≌△CEB,可求出∠CBE=∠ACD,则∠BCD+∠CBE=∠BCD+∠ACD=∠ACB.
E
D
B
C
A
随堂练习
3
解:∵△ABC是等边三角形,
∴∠ACB=∠A=∠ABC=60°,且AB=BC=AC.
∵在△ADC和△CEB中,
AC=CB,
∠A=∠BCE,
AD=CE,
∴△ADC≌△CEB(SAS),∠CBE=∠ACD.
∴∠BCD+∠CBE=∠BCD+∠ACD=∠ACB=60°.
E
D
B
C
A
如图,在等边三角形ABC中,D,E分别是AB,AC上的点,且AD=CE,则∠BCD+∠CBE的大小是多少?
正三角形ABC的两条角平分线BD和CE相交于点F,则∠BFC的度数是多少?
随堂练习
4
解:∵△ABC是正三角形,
∴∠ABC=∠ACB=60°.
∵BD和CE是正三角形ABC的角平分线,
∴∠ECB=30°,∠DBC=30°.
在△BFC中,∠BFC=180°-∠ECB-∠DBC
=180°-30°-30°
=120°.
A
B
C
D
E
F
课堂小结
等边
三角形
定义
性质
三边都相等的三角形.
三边相等,三个角相等,具有等腰三角形的一切性质.
拓展提升
1
如图,△ABC是等边三角形,△ADE是等腰三角形,AD=AE,∠DAE=80°,当DE⊥AC时,求∠BAD和∠EDC的度数.
分析:首先利用等腰三角形的性质得出
∠ADE=∠E=50°,∠DAF=∠EAF=40°,进而利用等边三角形各内角度数求出∠BAD即可,再利用三角形外角性质得出答案.
A
B
C
F
E
D
拓展提升
1
解:∵DE⊥AC,
∴∠DFA=∠EFA=90°.
∵AD=AE,∠DAE=80°,
∴∠ADE=∠E=50°.
∴∠DAF=∠EAF=40°.
∵△ABC是等边三角形,
∴∠BAC=60°.
∴∠BAD=∠BAC-∠DAF=20°.
∵∠B+∠BAD=∠ADC=∠ADE+∠EDC,
∴∠EDC=60°+20°-50°=30°.
如图,△ABC是等边三角形,△ADE是等腰三角形,AD=AE,∠DAE=80°,当DE⊥AC时,求∠BAD和∠EDC的度数.
A
B
C
F
E
D
拓展提升
2
如图,△ABC是边长为1的等边三角形,BD=CD,∠BDC=120°,点E,F分别在AB,AC上,且∠EDF=60°.求△AEF的周长.
分析:由∠BDC=120°和∠EDF=60°,得到
∠BDE+∠CDF=60°.想把这两个三角形拼在一起构造全等三角形,即延长AC至点P,使得CP=BE,证明△DEF≌△DPF,得到EF=PF,从而把△AEF的周长转化为△ABC的边长表示.
A
B
C
F
E
D
拓展提升
2
解:延长AC至点P,使得CP=BE,连接PD
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵BD=CD,∠BDC=120°,
∴∠DBC=∠DCB=30°.
∴∠EBD=∠DCF=90°.
∴∠DCP=∠DBE=90°.
在△BDE和△CDP中
,
BD=CD
∠DBE=∠DCP
BE=CP
∴△BDE≌△CDP.
C
P
A
B
F
E
如图,△ABC是边长为1的等边三角形,BD=CD,∠BDC=120°,点E,F分别在AB,AC上,且∠EDF=60°.求△AEF的周长.
D
拓展提升
2
∵△BDE≌△CDP,
∴DE=DP,∠BDE=∠CDP.
∵∠BDC=120°,
∠EDF=60°,
∴∠BDE+∠CDF=60°,∠CDP+∠CDF=60°.
∴∠EDF=∠PDF=60°.
在△DEF和△DPF中,
DE=DP,
∠EDF=∠PDF,
DF=DF,
∴△DEF≌△DPF.
∴EF=FP,EF=FC+BE.
∴△AEF的周长=AE+EF+AF=AE+FC+BE+AF=AB+AC=2.
C
A
B
F
E
D
P
