人教版八年级数学上册14.3.2公式法课件(21张PPT)
文档属性
| 名称 | 人教版八年级数学上册14.3.2公式法课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 123.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 00:00:00 | ||
图片预览




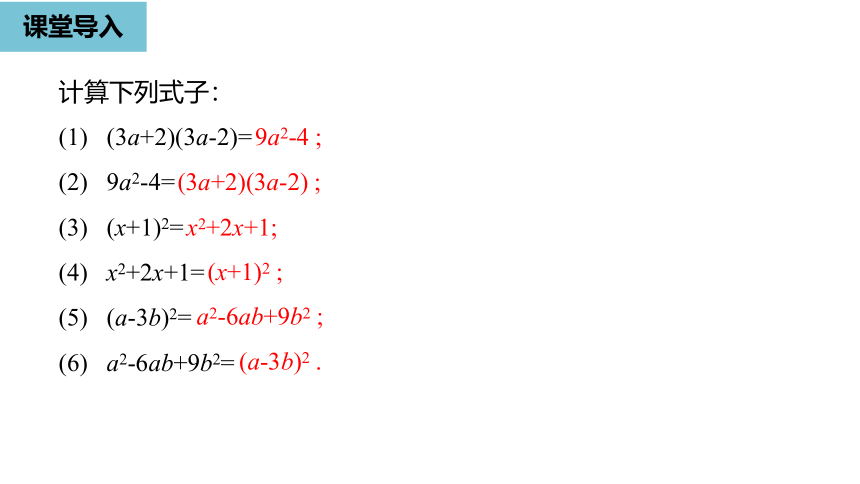




文档简介
(共21张PPT)
14.3.2 公式法
因式分解
知识回顾
因式分解:把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式.可以看出,因式分解与整式乘法是方向相反的变形,即
x2-1
(x+1)(x-1)
因式分解
整式乘法
知识回顾
提公因式法:
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另外一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
使用提公因式法分解因式时,所提的公因式必须是“最大公因式”,即提取公因式后,另一个因式中不再含有公因式.
学习目标
1、了解并掌握公式法分解因式的运算法则.
2、熟练运用公式法分解因式的运算法则进行实际的计算.
课堂导入
计算下列式子:
(1)
(3a+2)(3a-2)=
(2)
9a2-4=
(3)
(x+1)2=
(4)
x2+2x+1=
(5)
(a-3b)2=
(6)
a2-6ab+9b2=
9a2-4
;
(3a+2)(3a-2)
;
x2+2x+1;
(x+1)2
;
a2-6ab+9b2
;
(a-3b)2
.
知识点1
新知探究
平方差公式:由于整式的乘法与因式分解是方向相反的变形,把整式乘法的平方差公式(a+b)(a-b)=a2-b2的等号两边互换位置,就得到了a2-b2=(a+b)(a-b).
用平方差公式分解因式
“两个数”指的是a,b,而不是a2,b2,其中a,b可以是单项式,也可以是多项式.
语言叙述:两个数的平方差,等于这两个数的和与这两个数的差的积.
知识点1
新知探究
平方差公式的特点:
(1)
等号的左边是一个二项式,两项都是平方的形式且符号相反;
(2)
等号的右边是两个二项式的积,其中一个二项式是两个数的和,另一个二项式是这两个数的差.
用平方差公式分解因式
知识点1
新知探究
运用平方差公式的注意事项:
(1)
只有符合平方差公式特点的二项式,才可以运用平方差公式分解因式;
(2)
运用平方差公式分解因式的前提条件是多项式可以写成两个数(两个式子)的平方差的形式.
用平方差公式分解因式
知识点2
新知探究
完全平方式:我们把a2+2ab+b2和a2-2ab+b2这样的式子叫做完全平方式.
用完全平方公式分解因式
符合两个数的平方和加上(或减去)这两个数的积的2倍这个特点的式子就是完全平方式.
知识点2
新知探究
完全平方公式:把整式乘法的完全平方公式(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2
的等号两边互换位置,就可以得到:a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2.
用完全平方公式分解因式
语言叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
知识点2
新知探究
注意:
(1)
完全平方公式中的a和b可以是单项式,也可以是多项式;
(2)
利用完全平方公式可以把形如完全平方式的多项式分解因式;
(3)
因式分解中的完全平方公式与整式乘法中的完全平方公式的区别是等号两边的内容相反.
用完全平方公式分解因式
知识点2
新知探究
完全平方公式的特点:
(1)
等号左边是二次三项式,其中首尾两项分别是两个数(或两个式子)的平方,中间一项是这两个数(或者两个式子)的积的2倍,符号正负都可以;
(2)
等号的右边是这两个数(或两个式子)的平方,当等号左边中间的乘积项与首尾两项符号相同时,等号右边是两数和的平方;当等号左边中间的乘积项与首尾两项符号相反时,等号右边是两数差的平方.
用完全平方公式分解因式
知识点3
新知探究
公式法:如果把乘法公式的等号两边互换位置,就可以得到用于分解因式的公式,用来把某些具有特殊形式的多项式分解因式,这种分解因式的方法叫做公式法.
公式法分解因式
a2-b2=(a+b)(a-b)
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
知识点3
新知探究
因式分解的一般步骤:
(1)
当多项式的各项有公因式时,应先提取公因式;当多项式的各项没有公因式时(或提取公因式后),若符合平方差公式或完全平方公式,就利用公式法分解因式;
(2)
当不能直接提取公因式或用公式法分解因式时,可根据多项式的特点,把其变形为能提取公因式或能用公式法的形式,再分解因式;
(3)
当乘积中的每一个因式都不能再分解时,因式分解就结束了.
一提二套三彻底
公式法分解因式
例题解析
新知探究
分解因式
(1)
4x2-9
;
(2)
(x+p)2-(x+q)2
;
(3)
x4-y4
;
(4)
a3b-ab
.
解:
(1)
4x2-9=(2x)2-32=(2x+3)(2x-3)
;
(2)
(x+p)2-(x+q)2=[(x+p)+(x+q)][(x+p)-(x+q)]=(2x+p+q)(p-q)
;
例题解析
新知探究
解:
(3)
x4-y4=(x2)2-(y2)2=(x2+y2)(x2-y2)=(x2+y2)(x+y)(x-y)
;
(4)
a3b-ab=ab(a2-1)=ab(a+1)(a-1)
.
分解因式
(1)
4x2-9
;
(2)
(x+p)2-(x+q)2
;
(3)
x4-y4
;
(4)
a3b-ab
.
随堂练习
1
将下列各式分解因式:
(1)
4x2-25y2
;
(2)
(a+2)2-1
;
(3)
16(a-b)2-25(a+b)2
;
(4)
x5-16x
.
解:
(1)
4x2-25y2=(2x)2-(5y)2=(2x+5y)(2x-5y)
;
(2)
(a+2)2-1=(a+2+1)(a+2-1)=(a+3)(a+1)
;
随堂练习
1
解:
(3)
16(a-b)2-25(a+b)2
=[4(a-b)]2-[5(a+b)]2
=[4(a-b)+5(a+b)][4(a-b)-5(a+b)]
=(9a+b)(-a-9b)
=-(9a+b)(a+9b)
;
(4)
x5-16x
=x(x4-16)
=x[(x2)2-42]
=x(x2+4)(x2-4)
=x(x2+4)(x+2)(x-2)
.
将下列各式分解因式:
(1)
4x2-25y2
;
(2)
(a+2)2-1
;
(3)
16(a-b)2-25(a+b)2
;
(4)
x5-16x
.
课堂小结
因式分解
用平方差公式分解因式
用完全平方公式分解因式
因式分解的一般步骤
运用公式法分解因式计算法则
熟练进行计算
拓展提升
1
分解因式是解答整除问题的常用方法,通过因式分解,并结合数的奇偶性,先确定因式分解后的式子含有哪些因数,再根据倍数关系确定能被什么数整除.
已知k为正整数,试判断(2k+1)2-1能否被8整除,并说明理由.
拓展提升
1
解析:先利用因式分解将多项式化为积的形式,再观察其是不是8的倍数,从而进行说明.
解:(2k+1)2-1能被8整除,理由如下:
(2k+1)2-1=(2k+1+1)(2k+1-1)=(2k+2)·2k=4k(k+1).
因为k为正整数,所以k,k+1为两个相邻的正整数,
则其中必有一个为偶数,即2的倍数.
所以4k(k+1)为8的倍数,所以(2k+1)2-1能被8整除.
已知k为正整数,试判断(2k+1)2-1能否被8整除,并说明理由.
14.3.2 公式法
因式分解
知识回顾
因式分解:把一个多项式化成几个整式的积的形式,像这样的式子变形叫做这个多项式的因式分解,也叫做把这个多项式分解因式.可以看出,因式分解与整式乘法是方向相反的变形,即
x2-1
(x+1)(x-1)
因式分解
整式乘法
知识回顾
提公因式法:
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另外一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
使用提公因式法分解因式时,所提的公因式必须是“最大公因式”,即提取公因式后,另一个因式中不再含有公因式.
学习目标
1、了解并掌握公式法分解因式的运算法则.
2、熟练运用公式法分解因式的运算法则进行实际的计算.
课堂导入
计算下列式子:
(1)
(3a+2)(3a-2)=
(2)
9a2-4=
(3)
(x+1)2=
(4)
x2+2x+1=
(5)
(a-3b)2=
(6)
a2-6ab+9b2=
9a2-4
;
(3a+2)(3a-2)
;
x2+2x+1;
(x+1)2
;
a2-6ab+9b2
;
(a-3b)2
.
知识点1
新知探究
平方差公式:由于整式的乘法与因式分解是方向相反的变形,把整式乘法的平方差公式(a+b)(a-b)=a2-b2的等号两边互换位置,就得到了a2-b2=(a+b)(a-b).
用平方差公式分解因式
“两个数”指的是a,b,而不是a2,b2,其中a,b可以是单项式,也可以是多项式.
语言叙述:两个数的平方差,等于这两个数的和与这两个数的差的积.
知识点1
新知探究
平方差公式的特点:
(1)
等号的左边是一个二项式,两项都是平方的形式且符号相反;
(2)
等号的右边是两个二项式的积,其中一个二项式是两个数的和,另一个二项式是这两个数的差.
用平方差公式分解因式
知识点1
新知探究
运用平方差公式的注意事项:
(1)
只有符合平方差公式特点的二项式,才可以运用平方差公式分解因式;
(2)
运用平方差公式分解因式的前提条件是多项式可以写成两个数(两个式子)的平方差的形式.
用平方差公式分解因式
知识点2
新知探究
完全平方式:我们把a2+2ab+b2和a2-2ab+b2这样的式子叫做完全平方式.
用完全平方公式分解因式
符合两个数的平方和加上(或减去)这两个数的积的2倍这个特点的式子就是完全平方式.
知识点2
新知探究
完全平方公式:把整式乘法的完全平方公式(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2
的等号两边互换位置,就可以得到:a2+2ab+b2=(a+b)2,a2-2ab+b2=(a-b)2.
用完全平方公式分解因式
语言叙述:两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方.
知识点2
新知探究
注意:
(1)
完全平方公式中的a和b可以是单项式,也可以是多项式;
(2)
利用完全平方公式可以把形如完全平方式的多项式分解因式;
(3)
因式分解中的完全平方公式与整式乘法中的完全平方公式的区别是等号两边的内容相反.
用完全平方公式分解因式
知识点2
新知探究
完全平方公式的特点:
(1)
等号左边是二次三项式,其中首尾两项分别是两个数(或两个式子)的平方,中间一项是这两个数(或者两个式子)的积的2倍,符号正负都可以;
(2)
等号的右边是这两个数(或两个式子)的平方,当等号左边中间的乘积项与首尾两项符号相同时,等号右边是两数和的平方;当等号左边中间的乘积项与首尾两项符号相反时,等号右边是两数差的平方.
用完全平方公式分解因式
知识点3
新知探究
公式法:如果把乘法公式的等号两边互换位置,就可以得到用于分解因式的公式,用来把某些具有特殊形式的多项式分解因式,这种分解因式的方法叫做公式法.
公式法分解因式
a2-b2=(a+b)(a-b)
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
知识点3
新知探究
因式分解的一般步骤:
(1)
当多项式的各项有公因式时,应先提取公因式;当多项式的各项没有公因式时(或提取公因式后),若符合平方差公式或完全平方公式,就利用公式法分解因式;
(2)
当不能直接提取公因式或用公式法分解因式时,可根据多项式的特点,把其变形为能提取公因式或能用公式法的形式,再分解因式;
(3)
当乘积中的每一个因式都不能再分解时,因式分解就结束了.
一提二套三彻底
公式法分解因式
例题解析
新知探究
分解因式
(1)
4x2-9
;
(2)
(x+p)2-(x+q)2
;
(3)
x4-y4
;
(4)
a3b-ab
.
解:
(1)
4x2-9=(2x)2-32=(2x+3)(2x-3)
;
(2)
(x+p)2-(x+q)2=[(x+p)+(x+q)][(x+p)-(x+q)]=(2x+p+q)(p-q)
;
例题解析
新知探究
解:
(3)
x4-y4=(x2)2-(y2)2=(x2+y2)(x2-y2)=(x2+y2)(x+y)(x-y)
;
(4)
a3b-ab=ab(a2-1)=ab(a+1)(a-1)
.
分解因式
(1)
4x2-9
;
(2)
(x+p)2-(x+q)2
;
(3)
x4-y4
;
(4)
a3b-ab
.
随堂练习
1
将下列各式分解因式:
(1)
4x2-25y2
;
(2)
(a+2)2-1
;
(3)
16(a-b)2-25(a+b)2
;
(4)
x5-16x
.
解:
(1)
4x2-25y2=(2x)2-(5y)2=(2x+5y)(2x-5y)
;
(2)
(a+2)2-1=(a+2+1)(a+2-1)=(a+3)(a+1)
;
随堂练习
1
解:
(3)
16(a-b)2-25(a+b)2
=[4(a-b)]2-[5(a+b)]2
=[4(a-b)+5(a+b)][4(a-b)-5(a+b)]
=(9a+b)(-a-9b)
=-(9a+b)(a+9b)
;
(4)
x5-16x
=x(x4-16)
=x[(x2)2-42]
=x(x2+4)(x2-4)
=x(x2+4)(x+2)(x-2)
.
将下列各式分解因式:
(1)
4x2-25y2
;
(2)
(a+2)2-1
;
(3)
16(a-b)2-25(a+b)2
;
(4)
x5-16x
.
课堂小结
因式分解
用平方差公式分解因式
用完全平方公式分解因式
因式分解的一般步骤
运用公式法分解因式计算法则
熟练进行计算
拓展提升
1
分解因式是解答整除问题的常用方法,通过因式分解,并结合数的奇偶性,先确定因式分解后的式子含有哪些因数,再根据倍数关系确定能被什么数整除.
已知k为正整数,试判断(2k+1)2-1能否被8整除,并说明理由.
拓展提升
1
解析:先利用因式分解将多项式化为积的形式,再观察其是不是8的倍数,从而进行说明.
解:(2k+1)2-1能被8整除,理由如下:
(2k+1)2-1=(2k+1+1)(2k+1-1)=(2k+2)·2k=4k(k+1).
因为k为正整数,所以k,k+1为两个相邻的正整数,
则其中必有一个为偶数,即2的倍数.
所以4k(k+1)为8的倍数,所以(2k+1)2-1能被8整除.
已知k为正整数,试判断(2k+1)2-1能否被8整除,并说明理由.
