人教版八年级数学上册14.1.5整式的乘法课件(22张PPT)
文档属性
| 名称 | 人教版八年级数学上册14.1.5整式的乘法课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 128.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 13:02:11 | ||
图片预览








文档简介
(共22张PPT)
14.1.5 整式的乘法
整式的乘法与因式分解
知识回顾
单项式乘以单项式法则:一般地,单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(1)
单项式与单项式相乘的结果仍为单项式;
(2)
运用单项式乘法法则进行计算时,不能与合并同类项混淆;
(3)
只在一个单项式里面含有的字母,计算时不要遗漏.
知识回顾
单项式乘以多项式法则:一般地,单项式与多项式相乘,就是单项式去乘多项式的每一项,再把所得的积相加.
式子表示:p(a+b+c)=pa+pb+pc(p,a,b,c都是单项式).
多项式中的每一项都包括它前面的符号,根据去括号的法则,积的符号由单项式的符号与多项式的符号共同决定.
知识回顾
多项式乘以多项式法则:一般地,多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
式子表示:(a+b)(p+q)=ap+aq+bp+bq(a,b,p,q分别是单项式).
多项式与多项式相乘时,要按照一定的顺序进行,做到不重不漏.
学习目标
1、了解并掌握同底数幂的除法的运算法则.
2、掌握同底数幂的除法的运算法则的推导以及零指数幂的意义.
课堂导入
思考:如何计算am÷an(a≠0,m,n都是正整数,并且m>n).
根据除法是乘法的逆运算,计算被除数除以除数所得的商,就是求一个数,使它与除数的积等于被除数.
因为am-n·an=am-n+n=am,
所以am÷an=am-n.
新知探究
知识点1
性质:同底数幂相除,底数不变,指数相减.
符号表示:am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
同底数幂的除法
(1)
底数
a
可以是单项式,也可以是多项式,但不可以是
0;
(2)
同底数幂相除,底数不变,指数是相减而不是相除.
新知探究
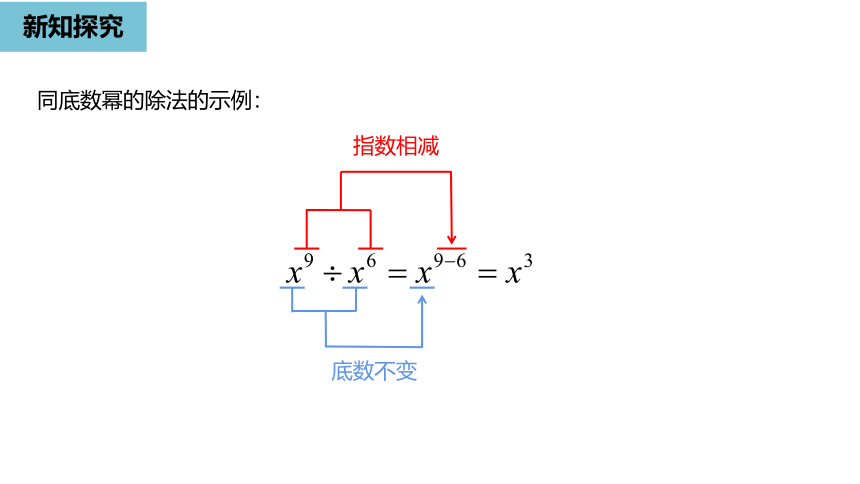
同底数幂的除法的示例:
底数不变
指数相减
新知探究
知识点2
性质:任何不等于0的数的零次幂都等于1.
符号表示:a0=1(a≠0).
零指数幂
(1)
零指数幂中的底数可以是单项式,也可以是多项式,但不可以是0;
(2)
因为
a=0
时,a0
无意义,所以
a0
有意义的条件是
a≠0,常据此确定底数中所含字母的取值范围.
新知探究
零指数幂的示例:
底数是-2
指数为0
结果为1
底数是100
指数为0
结果为1
新知探究
拓展:a0
=1
(a≠0)的推导过程:
当
m=n
时,am
÷an=am-n
=a0
,
因为
m=n
,
所以am
÷an
=1
.
则
a0
=1
.
随堂练习
1
计算下列式子:
(1)
(-xy)13÷(-xy)8
;
(2)
a2m+4÷am-2
;
(3)
(x-2y)3÷(2y-x)2
.
(2)
a2m+4÷am-2=a2m+4-m+2=am+6
;
解:(1)
(-xy)13÷(-xy)8=(-xy)13-8=(-xy)5
;
随堂练习
1
解:(3)
(x-2y)3÷(2y-x)2
=
(x-2y)3÷[-(x-2y)]2
=
(x-2y)3÷
(x-2y)2
=
x-2y
.
利用同底数幂的除法的性质运算时,底数不同时可以作适当的转化.
计算下列式子:
(1)
(-xy)13÷(-xy)8
;
(2)
a2m+4÷am-2
;
(3)
(x-2y)3÷(2y-x)2
.
随堂练习
2
若
(2x-6)0=1,则
x
的取值范围是(
)
A.
x≠0
B.
x≠3
C.
x=3
D.
x=0
解析:根据零指数幂的性质可知:2x-6≠0
,
所以x≠3
.
B
随堂练习
3
计算:(-a)3÷a
结果正确的是(
)
A.
a2
B.
-a2
C.
-a3
D.
-a4
解析:(-a)3÷a=-a3÷a=-a3-1=-a2
.
要注意a的指数为1,计算的时候不要遗漏.
B
随堂练习
4
计算:(-2018)0
的值是(
)
A.
-2018
B.
2018
C.
0
D.
1
D
解析:根据零指数幂的性质可知:任何不等于0的数的零次幂都等于1.
则
(-2018)0=1
.
随堂练习
5
已知
xm=9,xn=27,求
x3m-2n
的值.
解:x3m-2n=x3m÷x2n=(xm)3÷(xn)2,
因为
xm=9,
xn=27,
所以
x3m-2n=x3m÷x2n=(xm)3÷(xn)2
=93÷272
=(32)3÷(33)2
=1.
课堂小结
整式的乘法
同底数幂的除法的运算法则
零指数幂的意义
拓展提升
1
若
(1-x)1-3x=1,则
x
的取值有(
)
A.0个
B.1个
C.2个
D.3个
C
解析:根据零指数幂的意义可知:当1-3x=0且1-x≠0时,
(1-x)1-3x=1,此时
.
根据1的任意次幂仍然为1可知:当1-x=1时,
(1-x)1-3x=1.
此时x=0.
则满足条件的
x
的值有2个.
拓展提升
2
解关于
x
的方程
xm+3÷xm=x3+2x+4
.
解:xm+3÷xm=xm+3-m=x3,
也即
x3=x3+2x+4.
所以2x+4=0,解得x=-2.
拓展提升
3
若
32?92m+1÷27m+1=81,求m的值.
解:32?92m+1÷27m+1=32?(32)2m+1÷(33)m+1
=32?34m+2÷33m+3
=34m+4÷33m+3
=3m+1
.
因为
3m+1=81,所以m=3.
拓展提升
4
已知2x-5y=4,求
4x
÷32y
的值.
解:4x
÷32y=(22)x÷(25)y
=22x÷25y
=22x-5y
.
因为2x-5y=4,所以22x-5y=24=16,4x
÷32y=16.
14.1.5 整式的乘法
整式的乘法与因式分解
知识回顾
单项式乘以单项式法则:一般地,单项式与单项式相乘,把它们的系数、同底数幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.
(1)
单项式与单项式相乘的结果仍为单项式;
(2)
运用单项式乘法法则进行计算时,不能与合并同类项混淆;
(3)
只在一个单项式里面含有的字母,计算时不要遗漏.
知识回顾
单项式乘以多项式法则:一般地,单项式与多项式相乘,就是单项式去乘多项式的每一项,再把所得的积相加.
式子表示:p(a+b+c)=pa+pb+pc(p,a,b,c都是单项式).
多项式中的每一项都包括它前面的符号,根据去括号的法则,积的符号由单项式的符号与多项式的符号共同决定.
知识回顾
多项式乘以多项式法则:一般地,多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
式子表示:(a+b)(p+q)=ap+aq+bp+bq(a,b,p,q分别是单项式).
多项式与多项式相乘时,要按照一定的顺序进行,做到不重不漏.
学习目标
1、了解并掌握同底数幂的除法的运算法则.
2、掌握同底数幂的除法的运算法则的推导以及零指数幂的意义.
课堂导入
思考:如何计算am÷an(a≠0,m,n都是正整数,并且m>n).
根据除法是乘法的逆运算,计算被除数除以除数所得的商,就是求一个数,使它与除数的积等于被除数.
因为am-n·an=am-n+n=am,
所以am÷an=am-n.
新知探究
知识点1
性质:同底数幂相除,底数不变,指数相减.
符号表示:am÷an=am-n(a≠0,m,n都是正整数,并且m>n).
同底数幂的除法
(1)
底数
a
可以是单项式,也可以是多项式,但不可以是
0;
(2)
同底数幂相除,底数不变,指数是相减而不是相除.
新知探究
同底数幂的除法的示例:
底数不变
指数相减
新知探究
知识点2
性质:任何不等于0的数的零次幂都等于1.
符号表示:a0=1(a≠0).
零指数幂
(1)
零指数幂中的底数可以是单项式,也可以是多项式,但不可以是0;
(2)
因为
a=0
时,a0
无意义,所以
a0
有意义的条件是
a≠0,常据此确定底数中所含字母的取值范围.
新知探究
零指数幂的示例:
底数是-2
指数为0
结果为1
底数是100
指数为0
结果为1
新知探究
拓展:a0
=1
(a≠0)的推导过程:
当
m=n
时,am
÷an=am-n
=a0
,
因为
m=n
,
所以am
÷an
=1
.
则
a0
=1
.
随堂练习
1
计算下列式子:
(1)
(-xy)13÷(-xy)8
;
(2)
a2m+4÷am-2
;
(3)
(x-2y)3÷(2y-x)2
.
(2)
a2m+4÷am-2=a2m+4-m+2=am+6
;
解:(1)
(-xy)13÷(-xy)8=(-xy)13-8=(-xy)5
;
随堂练习
1
解:(3)
(x-2y)3÷(2y-x)2
=
(x-2y)3÷[-(x-2y)]2
=
(x-2y)3÷
(x-2y)2
=
x-2y
.
利用同底数幂的除法的性质运算时,底数不同时可以作适当的转化.
计算下列式子:
(1)
(-xy)13÷(-xy)8
;
(2)
a2m+4÷am-2
;
(3)
(x-2y)3÷(2y-x)2
.
随堂练习
2
若
(2x-6)0=1,则
x
的取值范围是(
)
A.
x≠0
B.
x≠3
C.
x=3
D.
x=0
解析:根据零指数幂的性质可知:2x-6≠0
,
所以x≠3
.
B
随堂练习
3
计算:(-a)3÷a
结果正确的是(
)
A.
a2
B.
-a2
C.
-a3
D.
-a4
解析:(-a)3÷a=-a3÷a=-a3-1=-a2
.
要注意a的指数为1,计算的时候不要遗漏.
B
随堂练习
4
计算:(-2018)0
的值是(
)
A.
-2018
B.
2018
C.
0
D.
1
D
解析:根据零指数幂的性质可知:任何不等于0的数的零次幂都等于1.
则
(-2018)0=1
.
随堂练习
5
已知
xm=9,xn=27,求
x3m-2n
的值.
解:x3m-2n=x3m÷x2n=(xm)3÷(xn)2,
因为
xm=9,
xn=27,
所以
x3m-2n=x3m÷x2n=(xm)3÷(xn)2
=93÷272
=(32)3÷(33)2
=1.
课堂小结
整式的乘法
同底数幂的除法的运算法则
零指数幂的意义
拓展提升
1
若
(1-x)1-3x=1,则
x
的取值有(
)
A.0个
B.1个
C.2个
D.3个
C
解析:根据零指数幂的意义可知:当1-3x=0且1-x≠0时,
(1-x)1-3x=1,此时
.
根据1的任意次幂仍然为1可知:当1-x=1时,
(1-x)1-3x=1.
此时x=0.
则满足条件的
x
的值有2个.
拓展提升
2
解关于
x
的方程
xm+3÷xm=x3+2x+4
.
解:xm+3÷xm=xm+3-m=x3,
也即
x3=x3+2x+4.
所以2x+4=0,解得x=-2.
拓展提升
3
若
32?92m+1÷27m+1=81,求m的值.
解:32?92m+1÷27m+1=32?(32)2m+1÷(33)m+1
=32?34m+2÷33m+3
=34m+4÷33m+3
=3m+1
.
因为
3m+1=81,所以m=3.
拓展提升
4
已知2x-5y=4,求
4x
÷32y
的值.
解:4x
÷32y=(22)x÷(25)y
=22x÷25y
=22x-5y
.
因为2x-5y=4,所以22x-5y=24=16,4x
÷32y=16.
