北师大版七年级下册专题学习——等腰三角形中常用作辅助线课件(16张PPT)
文档属性
| 名称 | 北师大版七年级下册专题学习——等腰三角形中常用作辅助线课件(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 237.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 23:58:25 | ||
图片预览




文档简介
(共16张PPT)
专题学习——等腰三角形中常用作辅助线
几何图形中添加辅助线,往往能把分散的条
件集中,使隐蔽的条件显露,将复杂的问题简单
化,例如:作“三线”中的“一线”,作平行线
构造等腰(边)三角形,利用截长补短法证线段和、
差关系或求角的度数,利用加倍折半法证线段的
倍分关系.
1
方法
作“三线”中的“一线”
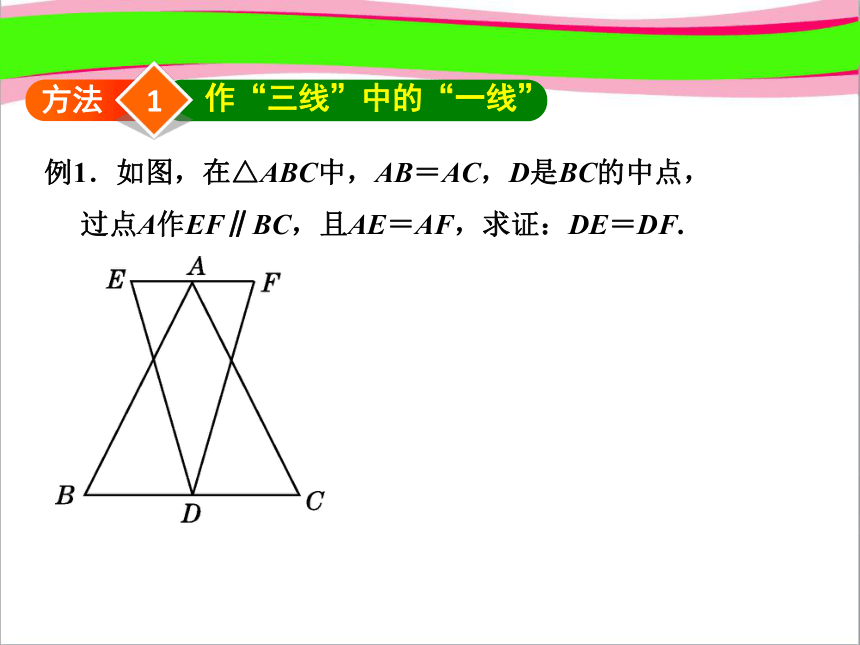
例1.如图,在△ABC中,AB=AC,D是BC的中点,
过点A作EF∥BC,且AE=AF,求证:DE=DF.
如图,连接AD.
∵AB=AC,BD=CD,
∴AD⊥BC.
∵EF∥BC,
∴AD⊥EF.
又∵AE=AF,
∴AD垂直平分EF.
∴DE=DF.
证明:
2
方法
作平行线法
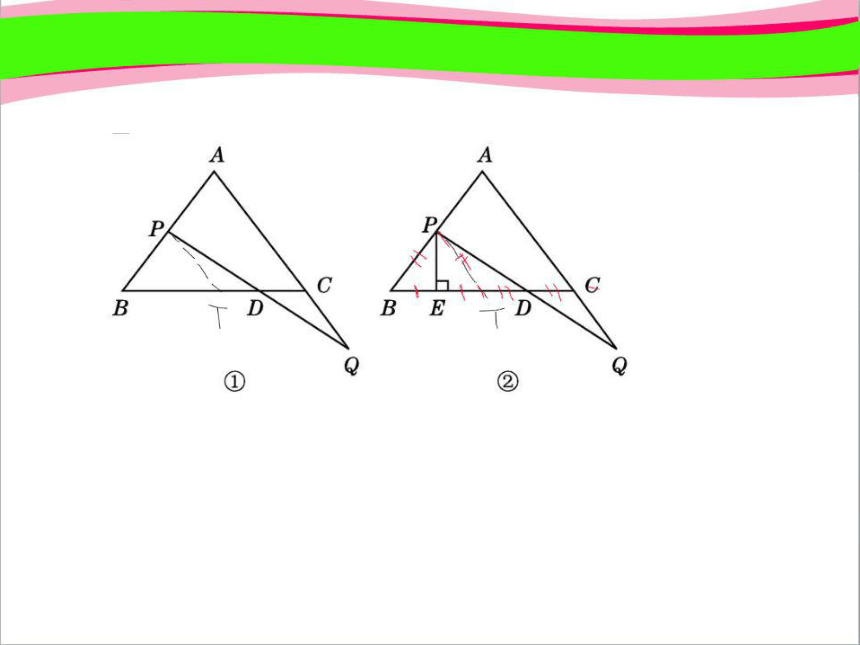
例2.如图,在△ABC中,AB=AC,点P从点B出发沿线段BA移动,同时,点Q从点C出发沿线段AC的延长线移动,点P,Q移动的速度相同,P,Q与直线BC相交于点D.
(1)如图①,求证:PD=QD;
(2)如图②,过点P作直线BC的垂线,垂足为E,当P,Q在移动的过程中,线段BE,DE,CD中是否存
在长度保持不变的线段?请说明理由.
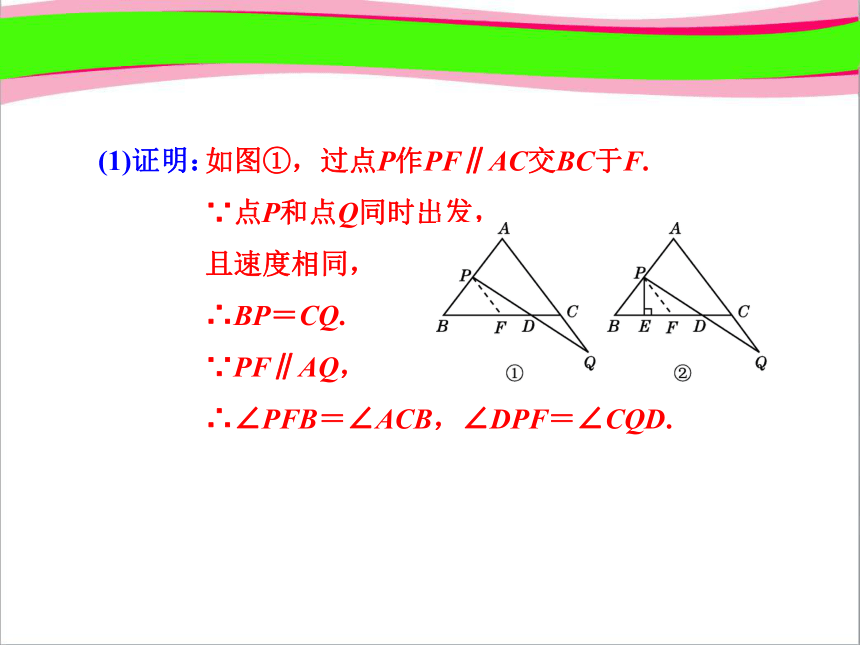
如图①,过点P作PF∥AC交BC于F.
∵点P和点Q同时出发,
且速度相同,
∴BP=CQ.
∵PF∥AQ,
∴∠PFB=∠ACB,∠DPF=∠CQD.
(1)证明:
又∵AB=AC,∴∠B=∠ACB.
∴∠B=∠PFB.
∴BP=PF.∴PF=CQ.
在△PFD和△QCD中,∠DPF=∠DQC,
∠PDF=∠QDC,PF=CQ,
∴△PFD≌△QCD(AAS),∴PD=QD.
ED的长度保持不变.理由如下:
如图②,过点P作PF∥AC交BC于F.
由(1)知PB=PF.∵PE⊥BF,
∴BE=EF.
由(1)知△PFD≌△QCD,∴FD=CD,
∴ED=EF+FD=BE+CD=
BC,
∴ED为定值.
(2)解:
3
方法
截长(补短)法
例3.如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.
求证:BD+DC=AB.
如图,延长BD至E,
使BE=AB,连接CE,AE.
∵∠ABE=60°,BE=AB,
∴△ABE为等边三角形.
∴∠AEB=60°.
又∵∠ACD=60°,
∴∠ACD=∠AEB.
∵AB=AC,AB=AE,
证明:
∴AC=AE.
∴∠ACE=∠AEC.
∴∠DCE=∠DEC.
∴DC=DE.
∴AB=BE=BD+DE=BD+CD,
即BD+DC=AB.
4
方法
加倍折半法
例4.如图,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,求∠C的度数.
在DC上截取DE=BD,连接AE,
∵AD⊥BC,BD=DE,
∴AD是线段BE的垂直平分线.
∴AB=AE,∴∠B=∠AEB.
∵AB+BD=CD,DE=BD,
∴AB+DE=CD.而CD=DE+EC,
∴AB=EC,∴AE=EC.
故设∠EAC=∠C=x,
解:
∵∠AEB为△AEC的外角,
∴∠AEB=∠EAC+∠C=2x,
∴∠B=2x,
∠BAE=180°-2x-2x=180°-4x.
∵∠BAC=120°,
∴∠BAE+∠EAC=120°,
即180°-4x+x=120°,
解得x=20°,则∠C=20°.
作业
《育才金典》126-128
专题学习——等腰三角形中常用作辅助线
几何图形中添加辅助线,往往能把分散的条
件集中,使隐蔽的条件显露,将复杂的问题简单
化,例如:作“三线”中的“一线”,作平行线
构造等腰(边)三角形,利用截长补短法证线段和、
差关系或求角的度数,利用加倍折半法证线段的
倍分关系.
1
方法
作“三线”中的“一线”
例1.如图,在△ABC中,AB=AC,D是BC的中点,
过点A作EF∥BC,且AE=AF,求证:DE=DF.
如图,连接AD.
∵AB=AC,BD=CD,
∴AD⊥BC.
∵EF∥BC,
∴AD⊥EF.
又∵AE=AF,
∴AD垂直平分EF.
∴DE=DF.
证明:
2
方法
作平行线法
例2.如图,在△ABC中,AB=AC,点P从点B出发沿线段BA移动,同时,点Q从点C出发沿线段AC的延长线移动,点P,Q移动的速度相同,P,Q与直线BC相交于点D.
(1)如图①,求证:PD=QD;
(2)如图②,过点P作直线BC的垂线,垂足为E,当P,Q在移动的过程中,线段BE,DE,CD中是否存
在长度保持不变的线段?请说明理由.
如图①,过点P作PF∥AC交BC于F.
∵点P和点Q同时出发,
且速度相同,
∴BP=CQ.
∵PF∥AQ,
∴∠PFB=∠ACB,∠DPF=∠CQD.
(1)证明:
又∵AB=AC,∴∠B=∠ACB.
∴∠B=∠PFB.
∴BP=PF.∴PF=CQ.
在△PFD和△QCD中,∠DPF=∠DQC,
∠PDF=∠QDC,PF=CQ,
∴△PFD≌△QCD(AAS),∴PD=QD.
ED的长度保持不变.理由如下:
如图②,过点P作PF∥AC交BC于F.
由(1)知PB=PF.∵PE⊥BF,
∴BE=EF.
由(1)知△PFD≌△QCD,∴FD=CD,
∴ED=EF+FD=BE+CD=
BC,
∴ED为定值.
(2)解:
3
方法
截长(补短)法
例3.如图,在△ABC中,AB=AC,D是△ABC外一点,且∠ABD=60°,∠ACD=60°.
求证:BD+DC=AB.
如图,延长BD至E,
使BE=AB,连接CE,AE.
∵∠ABE=60°,BE=AB,
∴△ABE为等边三角形.
∴∠AEB=60°.
又∵∠ACD=60°,
∴∠ACD=∠AEB.
∵AB=AC,AB=AE,
证明:
∴AC=AE.
∴∠ACE=∠AEC.
∴∠DCE=∠DEC.
∴DC=DE.
∴AB=BE=BD+DE=BD+CD,
即BD+DC=AB.
4
方法
加倍折半法
例4.如图,在△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,求∠C的度数.
在DC上截取DE=BD,连接AE,
∵AD⊥BC,BD=DE,
∴AD是线段BE的垂直平分线.
∴AB=AE,∴∠B=∠AEB.
∵AB+BD=CD,DE=BD,
∴AB+DE=CD.而CD=DE+EC,
∴AB=EC,∴AE=EC.
故设∠EAC=∠C=x,
解:
∵∠AEB为△AEC的外角,
∴∠AEB=∠EAC+∠C=2x,
∴∠B=2x,
∠BAE=180°-2x-2x=180°-4x.
∵∠BAC=120°,
∴∠BAE+∠EAC=120°,
即180°-4x+x=120°,
解得x=20°,则∠C=20°.
作业
《育才金典》126-128
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
