人教版八年级数学上册第十五章分式(小结复习2)课件(22张PPT)
文档属性
| 名称 | 人教版八年级数学上册第十五章分式(小结复习2)课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 93.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 13:02:45 | ||
图片预览








文档简介
(共22张PPT)
小结2
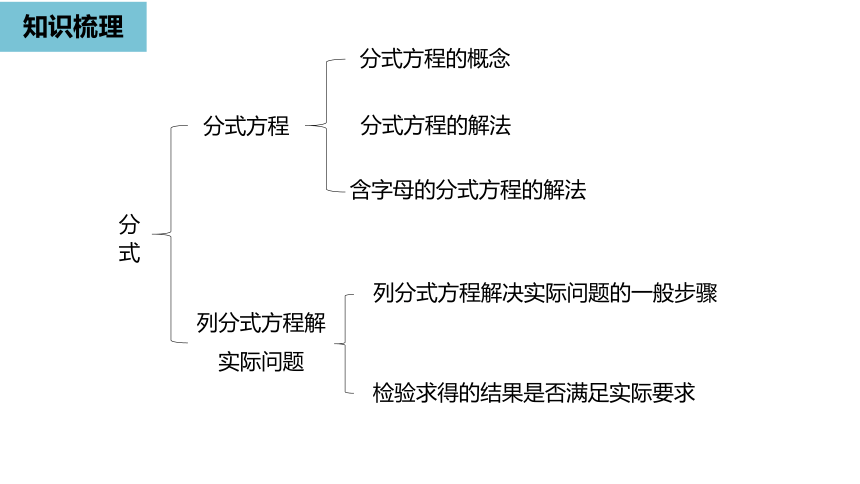
分式
知识梳理
分式
分式方程
列分式方程解
实际问题
分式方程的概念
含字母的分式方程的解法
列分式方程解决实际问题的一般步骤
检验求得的结果是否满足实际要求
分式方程的解法
知识梳理
分式方程的概念:分母中含有未知数的方程叫做分式方程.
分式方程必须满足的条件:(1)是方程;(2)含有分母;(3)分母中含有未知数.三者缺一不可.
知识梳理
解分式方程的一般步骤
知识梳理
(1)分式方程的增根:将分式方程转化为整式方程,若整式方程的解使得分式方程的最简公分母为0,则这个解叫做原分式方程的增根.
(2)产生增根的原因:分式方程本身就隐含着分母不为0的条件,当把分式方程转化为整式方程的时候,未知数的取值范围扩大,因此就有可能产生增根,增根一定适合分式方程转化后的整式方程,但增根不适合原分式方程,会使得原分式方程的分母为0.
分式方程的增根
知识梳理
含字母的分式方程的概念:若分式方程中除了含有表示未知数的字母外,还含有表示已知数的字母,则该方程是含有字母的分式方程.
含字母的分式方程的解法:含字母的分式方程与一般分式方程的解法相同,需要注意的是,要找准哪个字母表示未知数,哪个字母表示已知数,同时还要注意题目中所给的限制条件.
知识梳理
列分式方程解决实际问题的一般步骤
审:审清题意,找出题中的相等关系,分清题中的已知量、未知量;
设:设出恰当的未知数,注意单位和语言的完整性;
列:根据题中的相等关系,正确列出分式方程;
解:解所列分式方程;
验:既要检验所得的解是否为所列分式方程的解,又要检验所得的解是否符合实际问题的要求;
答:写出答案.
重点解析
1
解:(1)方程两边同时乘2(x-1),得2x=3-4(x-1),
整理得:6x=7,解得
.
检验:当
时,2(x-1)≠0,
所以原分式方程的解是
.
重点解析
1
方程两边同时乘x(x+2)(x-2),得3(x-2)-(x+2)=0,
整理得:2x-8=0,解得x=4.
检验:当x=4时,x(x+2)(x-2)≠0,
所以原分式方程的解是x=4.
重点解析
2
A.0或2
B.4
C.8
D.4或8
D
重点解析
3
班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发,苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.
问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
重点解析
3
解析:(1)设大巴的平均速度为
x
公里/时;
利用苏老师到达基地所用的时间和大巴到达基地所用的时间之间的关系列出分式方程即可.
(2)设苏老师追上大巴的地点距离基地的路程有
y
公里,则此时苏老师和大巴距离基地的路程都是
y
公里,也即是已经行驶了相同的路程;
利用苏老师的行驶时间和大巴的行驶时间之间的关系列出分式方程即可.
重点解析
3
解:(1)设大巴的平均速度为
x
公里/时,则小车的平均速度为1.5x
公里/时.
根据题意,得:
,
解得:x=40.
经检验:x=40是原分式方程的解,则1.5x=60.
答:大巴的平均速度为40公里/时,则小车的平均速度为60公里/时.
重点解析
3
解:(2)设苏老师追上大巴的地点距离基地的路程有
y
公里,则此时已经行驶了(90-y)公里.
根据题意,得:
,
解得:y=30.
答:苏老师追上大巴的地点距离基地的路程有30公里.
深化练习
1
解析:题目中x是未知数,a是已知数,
若原分式方程无解应分为两种情况:
(1)分式方程去分母化简成的整式方程无解;
(2)分式方程有增根.
要对两种情况分别进行讨论,否则得出的结果不正确.
若关于x的分式方程
无解,则a的值为____________.
深化练习
1
解:方程两边同时乘(x-3),得:x-3a=2a(x-3),
整理得:(1-2a)x=-3a,
(1)当1-2a=0时,整式方程无解,则原分式方程无解,此时
a=
;
(2)当1-2a≠0时,整式方程的解为x=
,
若分式方程无解,则x-3=0,解得x=3.将x=3代入得,a=1.
所以当a=1或
时,分式方程无解.
深化练习
2
解析:题目中x是未知数,a是已知数.
先将分式方程化为整式方程,解得的值是用a表示的式子,然后根据解为负数来确定a的取值范围.
注意:“解为负数”说明分式方程有解,所以化为整式方程后求得的x值需要进行验证.
深化练习
2
解:方程两边同时乘(x-2),得3x-a=x-2,
整理得:2x=a-2,解得
.
因为分式方程的解为负数,则有x<0,即
,
解得:a<2.
又因为x-2≠0,所以x≠2,即
,解得a≠6.
综上,a的取值范围是a<2.
深化练习
3
某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产多少个零件?规定的时间是多少天?
(2)为了提前完成生产任务,工厂在安排原有工人按原计划生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%.按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人有多少人?
深化练习
3
解析:(1)设原计划每天生产
x
个零件,因为生产的总量是24000个,所以生产时间可以用含有x的式子表示.
根据题目中相等关系“规定时间=实际时间”列方程.
(2)设原计划安排的工人有
y
人.
根据题目中相等关系“工人完成的零件个数+机器人完成的零件个数=24000”列方程.
深化练习
3
解:(1)设原计划每天生产
x
个零件.
根据题意,得:
,
解得:x=2400.
经检验:x=2400是原分式方程的解,且符合题意.
所以24000÷2400=10(天).
答:原计划每天生产2400个零件,规定的时间是10天.
深化练习
3
解:(2)设原计划安排的工人有
y
人.
根据题意,得:
,
解得:y=480.
经检验:y=480是原分式方程的解,且符合题意.
答:原计划安排的工人有480人.
小结2
分式
知识梳理
分式
分式方程
列分式方程解
实际问题
分式方程的概念
含字母的分式方程的解法
列分式方程解决实际问题的一般步骤
检验求得的结果是否满足实际要求
分式方程的解法
知识梳理
分式方程的概念:分母中含有未知数的方程叫做分式方程.
分式方程必须满足的条件:(1)是方程;(2)含有分母;(3)分母中含有未知数.三者缺一不可.
知识梳理
解分式方程的一般步骤
知识梳理
(1)分式方程的增根:将分式方程转化为整式方程,若整式方程的解使得分式方程的最简公分母为0,则这个解叫做原分式方程的增根.
(2)产生增根的原因:分式方程本身就隐含着分母不为0的条件,当把分式方程转化为整式方程的时候,未知数的取值范围扩大,因此就有可能产生增根,增根一定适合分式方程转化后的整式方程,但增根不适合原分式方程,会使得原分式方程的分母为0.
分式方程的增根
知识梳理
含字母的分式方程的概念:若分式方程中除了含有表示未知数的字母外,还含有表示已知数的字母,则该方程是含有字母的分式方程.
含字母的分式方程的解法:含字母的分式方程与一般分式方程的解法相同,需要注意的是,要找准哪个字母表示未知数,哪个字母表示已知数,同时还要注意题目中所给的限制条件.
知识梳理
列分式方程解决实际问题的一般步骤
审:审清题意,找出题中的相等关系,分清题中的已知量、未知量;
设:设出恰当的未知数,注意单位和语言的完整性;
列:根据题中的相等关系,正确列出分式方程;
解:解所列分式方程;
验:既要检验所得的解是否为所列分式方程的解,又要检验所得的解是否符合实际问题的要求;
答:写出答案.
重点解析
1
解:(1)方程两边同时乘2(x-1),得2x=3-4(x-1),
整理得:6x=7,解得
.
检验:当
时,2(x-1)≠0,
所以原分式方程的解是
.
重点解析
1
方程两边同时乘x(x+2)(x-2),得3(x-2)-(x+2)=0,
整理得:2x-8=0,解得x=4.
检验:当x=4时,x(x+2)(x-2)≠0,
所以原分式方程的解是x=4.
重点解析
2
A.0或2
B.4
C.8
D.4或8
D
重点解析
3
班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发,苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.
问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
重点解析
3
解析:(1)设大巴的平均速度为
x
公里/时;
利用苏老师到达基地所用的时间和大巴到达基地所用的时间之间的关系列出分式方程即可.
(2)设苏老师追上大巴的地点距离基地的路程有
y
公里,则此时苏老师和大巴距离基地的路程都是
y
公里,也即是已经行驶了相同的路程;
利用苏老师的行驶时间和大巴的行驶时间之间的关系列出分式方程即可.
重点解析
3
解:(1)设大巴的平均速度为
x
公里/时,则小车的平均速度为1.5x
公里/时.
根据题意,得:
,
解得:x=40.
经检验:x=40是原分式方程的解,则1.5x=60.
答:大巴的平均速度为40公里/时,则小车的平均速度为60公里/时.
重点解析
3
解:(2)设苏老师追上大巴的地点距离基地的路程有
y
公里,则此时已经行驶了(90-y)公里.
根据题意,得:
,
解得:y=30.
答:苏老师追上大巴的地点距离基地的路程有30公里.
深化练习
1
解析:题目中x是未知数,a是已知数,
若原分式方程无解应分为两种情况:
(1)分式方程去分母化简成的整式方程无解;
(2)分式方程有增根.
要对两种情况分别进行讨论,否则得出的结果不正确.
若关于x的分式方程
无解,则a的值为____________.
深化练习
1
解:方程两边同时乘(x-3),得:x-3a=2a(x-3),
整理得:(1-2a)x=-3a,
(1)当1-2a=0时,整式方程无解,则原分式方程无解,此时
a=
;
(2)当1-2a≠0时,整式方程的解为x=
,
若分式方程无解,则x-3=0,解得x=3.将x=3代入得,a=1.
所以当a=1或
时,分式方程无解.
深化练习
2
解析:题目中x是未知数,a是已知数.
先将分式方程化为整式方程,解得的值是用a表示的式子,然后根据解为负数来确定a的取值范围.
注意:“解为负数”说明分式方程有解,所以化为整式方程后求得的x值需要进行验证.
深化练习
2
解:方程两边同时乘(x-2),得3x-a=x-2,
整理得:2x=a-2,解得
.
因为分式方程的解为负数,则有x<0,即
,
解得:a<2.
又因为x-2≠0,所以x≠2,即
,解得a≠6.
综上,a的取值范围是a<2.
深化练习
3
某工厂计划在规定时间内生产24000个零件,若每天比原计划多生产30个零件,则在规定时间内可以多生产300个零件.
(1)求原计划每天生产多少个零件?规定的时间是多少天?
(2)为了提前完成生产任务,工厂在安排原有工人按原计划生产的同时,引进5组机器人生产流水线共同参与零件生产,已知每组机器人生产流水线每天生产零件的个数比20个工人原计划每天生产的零件总数还多20%.按此测算,恰好提前两天完成24000个零件的生产任务,求原计划安排的工人有多少人?
深化练习
3
解析:(1)设原计划每天生产
x
个零件,因为生产的总量是24000个,所以生产时间可以用含有x的式子表示.
根据题目中相等关系“规定时间=实际时间”列方程.
(2)设原计划安排的工人有
y
人.
根据题目中相等关系“工人完成的零件个数+机器人完成的零件个数=24000”列方程.
深化练习
3
解:(1)设原计划每天生产
x
个零件.
根据题意,得:
,
解得:x=2400.
经检验:x=2400是原分式方程的解,且符合题意.
所以24000÷2400=10(天).
答:原计划每天生产2400个零件,规定的时间是10天.
深化练习
3
解:(2)设原计划安排的工人有
y
人.
根据题意,得:
,
解得:y=480.
经检验:y=480是原分式方程的解,且符合题意.
答:原计划安排的工人有480人.
