人教版八年级数学上册15.2.1分式的乘除2课件(19张PPT)
文档属性
| 名称 | 人教版八年级数学上册15.2.1分式的乘除2课件(19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 148.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 11:45:37 | ||
图片预览






文档简介
(共19张PPT)
15.2.1分式的乘除
分式的运算
知识回顾
用式子表示:
分式的乘法法则:分式乘以分式,用分子的积作为积的分子,分母的积作为积的分母.
用式子表示:
分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
学习目标
1、了解并掌握分式的乘方法则.
2、能熟练运用分式的乘方法则进行计算,会分式的混合运算.
课堂导入
计算:
你能归纳出分式的
乘方的运算法则吗?
知识点1
新知探究
分式的乘方
分式的乘方法则:分式的乘方要把分子、分母分别乘方.
用式子表示:
(n为正整数).
a,b分别表示分子与分母,它们可以是单项式,也可以是多项式.
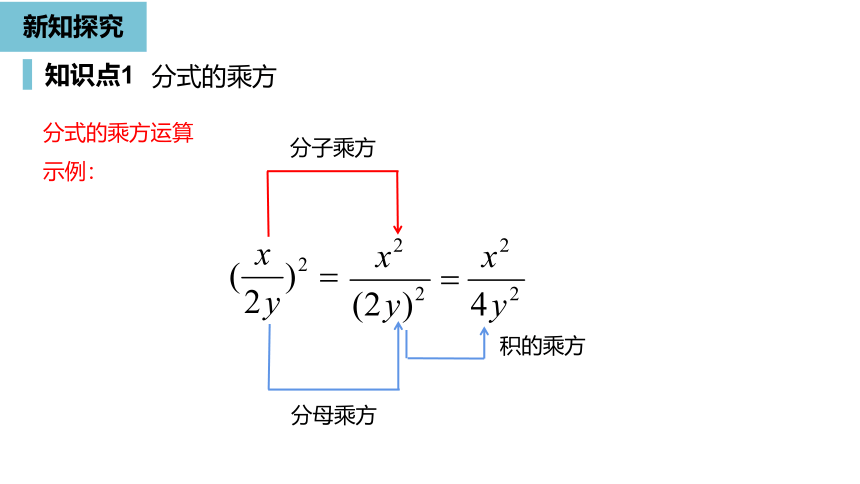
知识点1
新知探究
分式的乘方
分式的乘方运算
示例:
分母乘方
分子乘方
积的乘方
知识点1
新知探究
重点:(1)分式乘方时,确定乘方结果符号的方法与有理数乘方确定结果符号的方法相同:正分式的任何次幂都为正,负分式的偶次幂为正,奇次幂为负;
分式的乘方
(2)分式乘方时,一定要将分式加上括号,并且要将分子、分母分别乘方;
(3)分式乘方时,若分式的分子或分母是多项式,应把分子、分母分别看作一个整体乘方.
知识点2
新知探究
分式的乘除、乘方混合运算
分式的乘除混合运算:在运算时,乘除是同一级运算,若没有其他附加条件(如括号等),则应按照从左到右的顺序进行计算,若有括号,则先算括号里面的.一般地,乘除混合运算可以统一为乘法运算.
分式的乘除、乘方混合运算:分式的乘除、乘方混合运算顺序与分数的乘除、乘方混合运算顺序相同,即先乘方,再乘除,有括号的先算括号里面的.
知识点2
新知探究
分式的乘除、乘方混合运算
分式的乘除、乘方混合运算
示例:
先算乘方
除法化成乘法,将乘除混合运算统一为乘法运算.
随堂练习
1
计算:
(1)
(2)
解:(1)
(2)
随堂练习
2
计算:(1)
解:
随堂练习
2
计算:(2)
解:
随堂练习
3
计算:
原式=
第一步
第二步
回答:(1)上述过程中,第一步使用的公式用字母表示为(
);
(2)由第一步得到第二步所使用的运算方法是(
);
(3)以上两步中,第(
)步出现错误,本题的正确答案是(
).
随堂练习
3
计算:
原式=
随堂练习
3
回答:(1)上述过程中,第一步使用的公式用字母表示为
(
);
(2)由第一步得到第二步所使用的运算方法是(
);
(3)以上两步中,第(
)步出现错误,本题的正确答案是(
).
约分
二
-1
a2-2ab+b2=(a-b)2,a2-b2=(a+b)(a-b)
原式=
第一步
第二步
课堂小结
分式的运算
分式的乘方法则
分式的乘除、乘方
混合运算法则
熟练掌握分式的混合运算
拓展提升
1
已知a=b+2018,求
的值.
解:
∵a=b+2018,
∴
a-b=2018,
∴原式=2×2018=4036
.
拓展提升
2
解析:观察a2
+
b2
-
4a
+
6b
+13
=
0的形式,发现可以通过变形分别得到关于a,b的完全平方式,并能解得
a,b的值.再将要求的分式进行化简,代入a,b的值即可.
已知:a2
+
b2
-
4a
+
6b
+13
=
0,求
的值.
拓展提升
2
解:由a2
+
b2
-
4a
+
6b
+13
=
0
得:(a-2)2+(b+3)2
=
0.
由平方的非负性得:a=2,b=-3.
原式
将a=2,b=-3代入,原式=
.
已知:a2
+
b2
-
4a
+
6b
+13
=
0,求
的值.
15.2.1分式的乘除
分式的运算
知识回顾
用式子表示:
分式的乘法法则:分式乘以分式,用分子的积作为积的分子,分母的积作为积的分母.
用式子表示:
分式的除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘.
学习目标
1、了解并掌握分式的乘方法则.
2、能熟练运用分式的乘方法则进行计算,会分式的混合运算.
课堂导入
计算:
你能归纳出分式的
乘方的运算法则吗?
知识点1
新知探究
分式的乘方
分式的乘方法则:分式的乘方要把分子、分母分别乘方.
用式子表示:
(n为正整数).
a,b分别表示分子与分母,它们可以是单项式,也可以是多项式.
知识点1
新知探究
分式的乘方
分式的乘方运算
示例:
分母乘方
分子乘方
积的乘方
知识点1
新知探究
重点:(1)分式乘方时,确定乘方结果符号的方法与有理数乘方确定结果符号的方法相同:正分式的任何次幂都为正,负分式的偶次幂为正,奇次幂为负;
分式的乘方
(2)分式乘方时,一定要将分式加上括号,并且要将分子、分母分别乘方;
(3)分式乘方时,若分式的分子或分母是多项式,应把分子、分母分别看作一个整体乘方.
知识点2
新知探究
分式的乘除、乘方混合运算
分式的乘除混合运算:在运算时,乘除是同一级运算,若没有其他附加条件(如括号等),则应按照从左到右的顺序进行计算,若有括号,则先算括号里面的.一般地,乘除混合运算可以统一为乘法运算.
分式的乘除、乘方混合运算:分式的乘除、乘方混合运算顺序与分数的乘除、乘方混合运算顺序相同,即先乘方,再乘除,有括号的先算括号里面的.
知识点2
新知探究
分式的乘除、乘方混合运算
分式的乘除、乘方混合运算
示例:
先算乘方
除法化成乘法,将乘除混合运算统一为乘法运算.
随堂练习
1
计算:
(1)
(2)
解:(1)
(2)
随堂练习
2
计算:(1)
解:
随堂练习
2
计算:(2)
解:
随堂练习
3
计算:
原式=
第一步
第二步
回答:(1)上述过程中,第一步使用的公式用字母表示为(
);
(2)由第一步得到第二步所使用的运算方法是(
);
(3)以上两步中,第(
)步出现错误,本题的正确答案是(
).
随堂练习
3
计算:
原式=
随堂练习
3
回答:(1)上述过程中,第一步使用的公式用字母表示为
(
);
(2)由第一步得到第二步所使用的运算方法是(
);
(3)以上两步中,第(
)步出现错误,本题的正确答案是(
).
约分
二
-1
a2-2ab+b2=(a-b)2,a2-b2=(a+b)(a-b)
原式=
第一步
第二步
课堂小结
分式的运算
分式的乘方法则
分式的乘除、乘方
混合运算法则
熟练掌握分式的混合运算
拓展提升
1
已知a=b+2018,求
的值.
解:
∵a=b+2018,
∴
a-b=2018,
∴原式=2×2018=4036
.
拓展提升
2
解析:观察a2
+
b2
-
4a
+
6b
+13
=
0的形式,发现可以通过变形分别得到关于a,b的完全平方式,并能解得
a,b的值.再将要求的分式进行化简,代入a,b的值即可.
已知:a2
+
b2
-
4a
+
6b
+13
=
0,求
的值.
拓展提升
2
解:由a2
+
b2
-
4a
+
6b
+13
=
0
得:(a-2)2+(b+3)2
=
0.
由平方的非负性得:a=2,b=-3.
原式
将a=2,b=-3代入,原式=
.
已知:a2
+
b2
-
4a
+
6b
+13
=
0,求
的值.
