湘教版九年级数学下册 1.4二次函数与一元二次方程的联系 同步练习及答案
文档属性
| 名称 | 湘教版九年级数学下册 1.4二次函数与一元二次方程的联系 同步练习及答案 |  | |
| 格式 | zip | ||
| 文件大小 | 77.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 10:19:45 | ||
图片预览



文档简介
第1章 二次函数
1.4 二次函数与一元二次方程的联系
1.
一元二次方程2x2-3x-5=0的两根是、-1,则二次函数y=2x2-3x-5的图象与x轴的两个交点间的距离为(
)
A.2
B.
C.
D.5
2.抛物线y=x2+2x+m-1与x轴有两个不同的交点,则m的取值范围是(
)
A.
m<2
B.
m>2
C.
0<m≤2
D.
m<-2
3.
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是(
)
A.
a>0
B.
当x>1时,y随x的增大而增大
C.
c<0
D.
3是方程ax2+bx+c=0的一个根
4.
抛物线y=ax2+2ax+c与x轴的一个交点为(-5,0),则它与x轴的另一个交点的坐标为(
)
A.(3,0)
B.(-3,0)
C.(,0)
D.不能确定,与a的值有关
5.
抛物线y=2x2-2x+1与坐标轴的交点个数是(
)
A.
0
B.
2
C.
3
D.
4
6.
已知二次函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围是(
)
A.
k<4
B.
k≤4
C.
k<4且k≠3
D.
k≤4且k≠3
7.
下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,正确的是(
)
A.没有交点
B.只有一个交点,且它位于y轴右侧
C.有两个交点,且它们均位于y轴左侧
D.有两个交点,且它们均位于y轴右侧
8.
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大.其中结论正确的个数是(
)
A.4个
B.3个
C.2个
D.1个
9.
如果抛物线y=ax2+bx+c与x轴有公共点,公共点的横坐标是x0,那么当x=
时,函数的值是0,因此x=
就是方程ax2+bx+c=0的一个根.
10.
抛物线y=2(x+3)(x-2)与x轴的交点坐标分别为
.
11.抛物线y=2x2+8x+m与x轴只有一个公共点,则m的值为
.
12.抛物线y=-x2+bx+c的图象如图所示,关于x的一元二次方程-x2+bx+c=0的解是
.
13.
已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,若点A的坐标为(-2,0),抛物线的对称轴为直线x=2,则线段AB的长为
.
14.二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx=0的根是
.
15.
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-(x-4)2+3,由此可知铅球推出的距离是
.
16.
二次函数y=x2+(2a+1)x+(a-2)2,a取何值时.
(1)
抛物线与x轴有两个交点;
(2)
抛物线与x轴只有一个交点;
(3)
抛物线与x轴无交点.
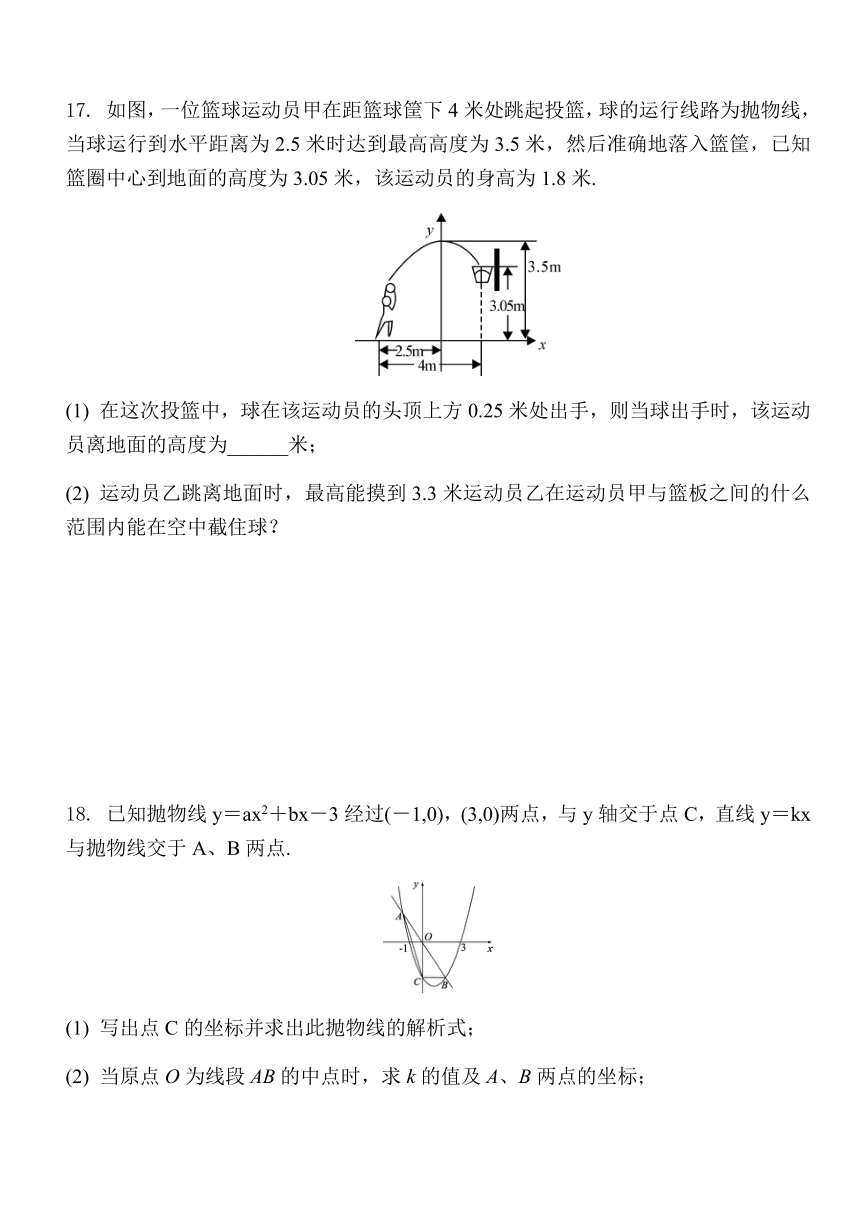
17.
如图,一位篮球运动员甲在距篮球筐下4米处跳起投篮,球的运行线路为抛物线,当球运行到水平距离为2.5米时达到最高高度为3.5米,然后准确地落入篮筐,已知篮圈中心到地面的高度为3.05米,该运动员的身高为1.8米.
(1)
在这次投篮中,球在该运动员的头顶上方0.25米处出手,则当球出手时,该运动员离地面的高度为______米;
(2)
运动员乙跳离地面时,最高能摸到3.3米运动员乙在运动员甲与篮板之间的什么范围内能在空中截住球?
18.
已知抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A、B两点.
(1)
写出点C的坐标并求出此抛物线的解析式;
(2)
当原点O为线段AB的中点时,求k的值及A、B两点的坐标;
(3)
是否存在实数k使得△ABC的面积为?若存在,求出k的值;若不存在,请说明理由.
答案:
1---8
CADAB
DDB
9.
x0
x0
10.
(-3,0)(2,0)
11.
8
12.
x1=3 x2=-1
13.
8
14.
x1=0,x2=2
15.
10
16.
解:△=(2a+1)2-4×1×(a-2)2=20a-15
(1)△>0即:a>;
(2)△=0即:a=;
(3)△<0即:a<.
17.
(1)解:设抛物线的解析式为y=ax2+3.5,∵(1.5,3.05)在抛物线上,
∴3.05=a×1.52+3.5,解得a=-0.2,∴y=-0.2x2+3.5;
当x=-2.5时,y=2.25,∴运动员离地面的高度为2.25-0.25-1.8=0.2m,
故答案为0.2;
(2)由题意可得出:y=3.3,则3.3=-0.2x2+3.5,解得:x1=1,x2=-1,
∴4-1=3m,∴乙在运动员甲与篮板之间的距离甲3米范围内能在空中截住球.
18.
解:(1)
令抛物线y=ax2+bx-3中x=0,则y=-3,∴点C的坐标为(0,-3),∵抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,∴有,解得,∴此抛物线的解析式为y=x2-2x-3;
(2)
解:将y=kx代入y=x2-2x-3中得:kx=x2-2x-3,整理得:x2-(2+k)x-3=0,∴xA+xB=2+k,xA·xB=-3,∵原点O为线段AB的中点,∴xA+xB=2+k=0,解得:k=-2.当k=-2时,x2-(2+k)x-3=x2-3=0,解得:xA=-,xB=.∴yA=-2xA=2,yB=-2xB=-2.故当原点O为线段AB的中点时,k的值为-2,点A的坐标为(-,2),点B的坐标为(,-2);
(3)
解:假设存在.由(2)可知:xA+xB=2+k,xA·xB=-3,S△ABC=OC·|xA-xB|=×3×=,∴(2+k)2-4×(-3)=10,即(2+k)2+2=0,∵(2+k)2非负,无解.故假设不成了.所以不存在实数k使得△ABC的面积为.
1.4 二次函数与一元二次方程的联系
1.
一元二次方程2x2-3x-5=0的两根是、-1,则二次函数y=2x2-3x-5的图象与x轴的两个交点间的距离为(
)
A.2
B.
C.
D.5
2.抛物线y=x2+2x+m-1与x轴有两个不同的交点,则m的取值范围是(
)
A.
m<2
B.
m>2
C.
0<m≤2
D.
m<-2
3.
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是(
)
A.
a>0
B.
当x>1时,y随x的增大而增大
C.
c<0
D.
3是方程ax2+bx+c=0的一个根
4.
抛物线y=ax2+2ax+c与x轴的一个交点为(-5,0),则它与x轴的另一个交点的坐标为(
)
A.(3,0)
B.(-3,0)
C.(,0)
D.不能确定,与a的值有关
5.
抛物线y=2x2-2x+1与坐标轴的交点个数是(
)
A.
0
B.
2
C.
3
D.
4
6.
已知二次函数y=(k-3)x2+2x+1的图象与x轴有交点,则k的取值范围是(
)
A.
k<4
B.
k≤4
C.
k<4且k≠3
D.
k≤4且k≠3
7.
下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,正确的是(
)
A.没有交点
B.只有一个交点,且它位于y轴右侧
C.有两个交点,且它们均位于y轴左侧
D.有两个交点,且它们均位于y轴右侧
8.
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:①4ac<b2;②方程ax2+bx+c=0的两个根是x1=-1,x2=3;③3a+c>0;④当y>0时,x的取值范围是-1≤x<3;⑤当x<0时,y随x增大而增大.其中结论正确的个数是(
)
A.4个
B.3个
C.2个
D.1个
9.
如果抛物线y=ax2+bx+c与x轴有公共点,公共点的横坐标是x0,那么当x=
时,函数的值是0,因此x=
就是方程ax2+bx+c=0的一个根.
10.
抛物线y=2(x+3)(x-2)与x轴的交点坐标分别为
.
11.抛物线y=2x2+8x+m与x轴只有一个公共点,则m的值为
.
12.抛物线y=-x2+bx+c的图象如图所示,关于x的一元二次方程-x2+bx+c=0的解是
.
13.
已知抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点,若点A的坐标为(-2,0),抛物线的对称轴为直线x=2,则线段AB的长为
.
14.二次函数y=ax2+bx+3的图象经过点A(-1,0),B(3,0),那么一元二次方程ax2+bx=0的根是
.
15.
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-(x-4)2+3,由此可知铅球推出的距离是
.
16.
二次函数y=x2+(2a+1)x+(a-2)2,a取何值时.
(1)
抛物线与x轴有两个交点;
(2)
抛物线与x轴只有一个交点;
(3)
抛物线与x轴无交点.
17.
如图,一位篮球运动员甲在距篮球筐下4米处跳起投篮,球的运行线路为抛物线,当球运行到水平距离为2.5米时达到最高高度为3.5米,然后准确地落入篮筐,已知篮圈中心到地面的高度为3.05米,该运动员的身高为1.8米.
(1)
在这次投篮中,球在该运动员的头顶上方0.25米处出手,则当球出手时,该运动员离地面的高度为______米;
(2)
运动员乙跳离地面时,最高能摸到3.3米运动员乙在运动员甲与篮板之间的什么范围内能在空中截住球?
18.
已知抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A、B两点.
(1)
写出点C的坐标并求出此抛物线的解析式;
(2)
当原点O为线段AB的中点时,求k的值及A、B两点的坐标;
(3)
是否存在实数k使得△ABC的面积为?若存在,求出k的值;若不存在,请说明理由.
答案:
1---8
CADAB
DDB
9.
x0
x0
10.
(-3,0)(2,0)
11.
8
12.
x1=3 x2=-1
13.
8
14.
x1=0,x2=2
15.
10
16.
解:△=(2a+1)2-4×1×(a-2)2=20a-15
(1)△>0即:a>;
(2)△=0即:a=;
(3)△<0即:a<.
17.
(1)解:设抛物线的解析式为y=ax2+3.5,∵(1.5,3.05)在抛物线上,
∴3.05=a×1.52+3.5,解得a=-0.2,∴y=-0.2x2+3.5;
当x=-2.5时,y=2.25,∴运动员离地面的高度为2.25-0.25-1.8=0.2m,
故答案为0.2;
(2)由题意可得出:y=3.3,则3.3=-0.2x2+3.5,解得:x1=1,x2=-1,
∴4-1=3m,∴乙在运动员甲与篮板之间的距离甲3米范围内能在空中截住球.
18.
解:(1)
令抛物线y=ax2+bx-3中x=0,则y=-3,∴点C的坐标为(0,-3),∵抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,∴有,解得,∴此抛物线的解析式为y=x2-2x-3;
(2)
解:将y=kx代入y=x2-2x-3中得:kx=x2-2x-3,整理得:x2-(2+k)x-3=0,∴xA+xB=2+k,xA·xB=-3,∵原点O为线段AB的中点,∴xA+xB=2+k=0,解得:k=-2.当k=-2时,x2-(2+k)x-3=x2-3=0,解得:xA=-,xB=.∴yA=-2xA=2,yB=-2xB=-2.故当原点O为线段AB的中点时,k的值为-2,点A的坐标为(-,2),点B的坐标为(,-2);
(3)
解:假设存在.由(2)可知:xA+xB=2+k,xA·xB=-3,S△ABC=OC·|xA-xB|=×3×=,∴(2+k)2-4×(-3)=10,即(2+k)2+2=0,∵(2+k)2非负,无解.故假设不成了.所以不存在实数k使得△ABC的面积为.
