冀教版八年级数学下册21.2一次函数图象与性质--图像的平移课件(共19张PPT)
文档属性
| 名称 | 冀教版八年级数学下册21.2一次函数图象与性质--图像的平移课件(共19张PPT) | 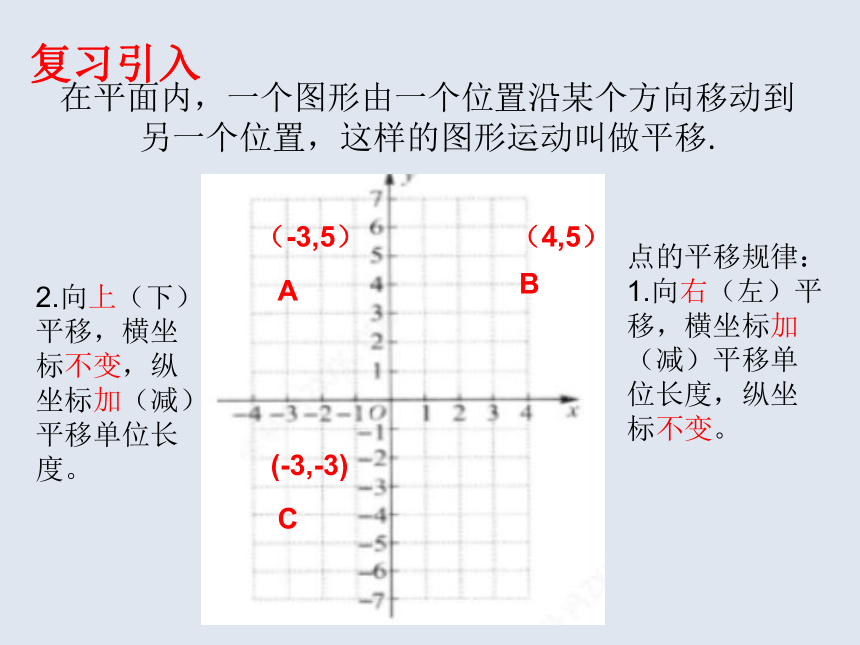 | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 11:57:41 | ||
图片预览






文档简介
(共19张PPT)
在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动叫做平移.
(-3,5)
(4,5)
(-3,-3)
A
B
C
点的平移规律:
1.向右(左)平移,横坐标加(减)平移单位长度,纵坐标不变。
2.向上(下)平移,横坐标不变,纵坐标加(减)平移单位长度。
复习引入
一次函数图象的
平移问题
专题学习
学习目标
1.能够掌握直线平移的推导过程,体会不同情况下平移的移动规律。
2.能够灵活运用平移规律解决数学问题。
3.简单体会显性平移和隐性平移的区别。
y
-4
-2
-3
-1
3
2
1
-1
0
-2
1
2
3
4
5
x
-5
y=2x
y=2x+3
y=2x-2
y=2x
y=2x+3
y=2x
-2
(0,0)
(1,2)
(0,3)
(-1.5,0)
(0,-2)
(1,0)
例
在同一坐标系内作出下列函数
y=2x,
y=2x+3,y=2x-2的图象。
2
2
2
k相等
平行
规律探究
1.直线y=2x过
(0,0).
(0,3)
3
(0,-2)
2
上
下
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
规律探究
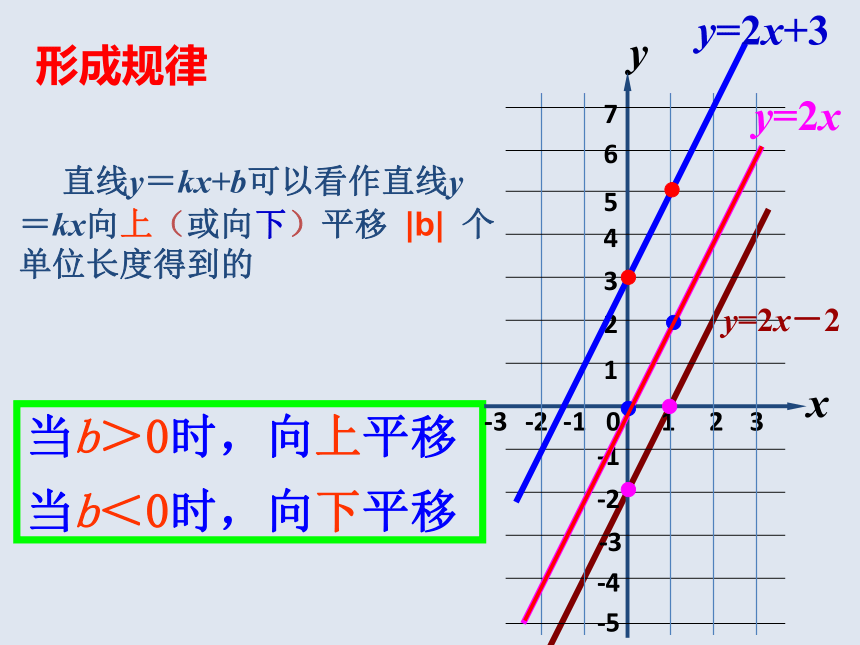
直线y=kx+b可以看作直线y=kx向上(或向下)平移
|b|
个单位长度得到的
当b<0时,向下平移
当b>0时,向上平移
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
形成规律
y
=x
y=x+2
y
=x-2
y
2
0
仔细观察,y=kx+b
中的b有什么作用?
-2
.
.
向上平移或向下平移是由常量b来决定的.+2时向上平移2个单位,-2时向下平移2个单位.
“上加下减”
规律深究
【记】一次函数y=kx+b向上平移m(m≥0)个单位长度,平移后的一次函数为y=kx+b+m;向下平移m(m≥0)个单位长度,平移后的一次函数为y=kx+b-m.
(1)图像的上下平移与k无关。
(2)图像的上下平移与b有关。
简称:上加下减.
规律小结
1.直线y=3x-2可由直线y=3x向
平移
单位得到.
2.直线y=x+2可由直线y=x-1向
平移
单位得到.
2
下
3
上
追踪练习
3.将直线y=5x向
平移
个单位长度得到直线y=5x+7.
4.将直线y=3x+3向
平移
个单位长度得到直线y=3x-2.
上
7
下
5
-6
o
-4
4
6
2
4
6
-2
-2
-4
x
y
2
问题:把一次函数y=2x向右平移4个单位,可得到新的函数关系式
8
6
8
y=2x
(4,0)
(6,4)
规律再探
1.y=2x与y=2x-8之间有什么联系?
2.y=2x-8可以怎样变形出现平移单位4?
y=2(
x-
4
)
一次函数图像的左右平移与自变量x有关,向右移动x的值减小。
探究规律
y=2x-8
一般地,把y=kx+b向右平移m(m>0)个单位,求得到的新的函数关系式是多少?
x
y
0
形成规律
【记】一次函数y=kx+b向左m(m≥0)个单位长度后,得到的一次函数为y=k(x+m)+b;一次函数y=kx+b向右m(m≥0)个单位长度后得到的一次函数为y=k(x-m)+b.
(1)图像的左右平移与K、b均无关
(2)图像的左右平移与自变量x有关,
向左移动x的值增加,向右移动x的值减小
。
简称
“左加右减”
规律小结
规律总结
简记为“左加右减,上加下减”(左右平移只给x加减,上下平移等号右边整体加减)
【记】
1.将直线y=-7x向左平移2个单位,可得到新的函数关系式为
y=-7x-14
2、把一次函数y=2x-1沿x轴向左平移1个单位,得到的直线解析式是
3.将直线y=-3x+1向右平移1个单位,可得到新的函数关系式为
4.把一次函数y=-2x+2沿x轴向右平移2个单位,得到的直线解析式是
追踪练习
y=2x+1
y=-3x+4
y=-2x+6
显性平移与隐性平移
1.一次函数y=kx+b(k≠0)的图象过点A(0,2),B(3,0),若将该图象沿x轴向左平移2个单位,则新图象对应的解析式为
(.y=-
2/3x+
2/3)
综合运用
2、已知一次函数y=kx+b的图象是过A(0,-4),B(2,-3)两点的一条直线.
(1)求直线AB的解析式;
(2)将直线AB向左平移6个单位,求平移后的直线的解析式.
(3)将直线AB向上平移6个单位,求原点到平移后的直线的距离.
综合运用
学习目标
课堂小结
1.能够掌握直线平移的推导过程,体会不同情况下平移的移动规律。
2.能够灵活运用平移规律解决数学问题。
3.简单体会显性平移和隐性平移的区别。
(1)一次函数中两直线平行:k相等
(2)一次函数上下平移遵循:上加下减
(3)一次函数左右平移遵循:左加右减
在平面内,一个图形由一个位置沿某个方向移动到另一个位置,这样的图形运动叫做平移.
(-3,5)
(4,5)
(-3,-3)
A
B
C
点的平移规律:
1.向右(左)平移,横坐标加(减)平移单位长度,纵坐标不变。
2.向上(下)平移,横坐标不变,纵坐标加(减)平移单位长度。
复习引入
一次函数图象的
平移问题
专题学习
学习目标
1.能够掌握直线平移的推导过程,体会不同情况下平移的移动规律。
2.能够灵活运用平移规律解决数学问题。
3.简单体会显性平移和隐性平移的区别。
y
-4
-2
-3
-1
3
2
1
-1
0
-2
1
2
3
4
5
x
-5
y=2x
y=2x+3
y=2x-2
y=2x
y=2x+3
y=2x
-2
(0,0)
(1,2)
(0,3)
(-1.5,0)
(0,-2)
(1,0)
例
在同一坐标系内作出下列函数
y=2x,
y=2x+3,y=2x-2的图象。
2
2
2
k相等
平行
规律探究
1.直线y=2x过
(0,0).
(0,3)
3
(0,-2)
2
上
下
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
规律探究
直线y=kx+b可以看作直线y=kx向上(或向下)平移
|b|
个单位长度得到的
当b<0时,向下平移
当b>0时,向上平移
y
-4
-2
-3
-1
3
2
1
-1
0
-2
-3
1
2
3
4
5
x
6
7
-5
y=2x
y=2x+3
y=2x-2
形成规律
y
=x
y=x+2
y
=x-2
y
2
0
仔细观察,y=kx+b
中的b有什么作用?
-2
.
.
向上平移或向下平移是由常量b来决定的.+2时向上平移2个单位,-2时向下平移2个单位.
“上加下减”
规律深究
【记】一次函数y=kx+b向上平移m(m≥0)个单位长度,平移后的一次函数为y=kx+b+m;向下平移m(m≥0)个单位长度,平移后的一次函数为y=kx+b-m.
(1)图像的上下平移与k无关。
(2)图像的上下平移与b有关。
简称:上加下减.
规律小结
1.直线y=3x-2可由直线y=3x向
平移
单位得到.
2.直线y=x+2可由直线y=x-1向
平移
单位得到.
2
下
3
上
追踪练习
3.将直线y=5x向
平移
个单位长度得到直线y=5x+7.
4.将直线y=3x+3向
平移
个单位长度得到直线y=3x-2.
上
7
下
5
-6
o
-4
4
6
2
4
6
-2
-2
-4
x
y
2
问题:把一次函数y=2x向右平移4个单位,可得到新的函数关系式
8
6
8
y=2x
(4,0)
(6,4)
规律再探
1.y=2x与y=2x-8之间有什么联系?
2.y=2x-8可以怎样变形出现平移单位4?
y=2(
x-
4
)
一次函数图像的左右平移与自变量x有关,向右移动x的值减小。
探究规律
y=2x-8
一般地,把y=kx+b向右平移m(m>0)个单位,求得到的新的函数关系式是多少?
x
y
0
形成规律
【记】一次函数y=kx+b向左m(m≥0)个单位长度后,得到的一次函数为y=k(x+m)+b;一次函数y=kx+b向右m(m≥0)个单位长度后得到的一次函数为y=k(x-m)+b.
(1)图像的左右平移与K、b均无关
(2)图像的左右平移与自变量x有关,
向左移动x的值增加,向右移动x的值减小
。
简称
“左加右减”
规律小结
规律总结
简记为“左加右减,上加下减”(左右平移只给x加减,上下平移等号右边整体加减)
【记】
1.将直线y=-7x向左平移2个单位,可得到新的函数关系式为
y=-7x-14
2、把一次函数y=2x-1沿x轴向左平移1个单位,得到的直线解析式是
3.将直线y=-3x+1向右平移1个单位,可得到新的函数关系式为
4.把一次函数y=-2x+2沿x轴向右平移2个单位,得到的直线解析式是
追踪练习
y=2x+1
y=-3x+4
y=-2x+6
显性平移与隐性平移
1.一次函数y=kx+b(k≠0)的图象过点A(0,2),B(3,0),若将该图象沿x轴向左平移2个单位,则新图象对应的解析式为
(.y=-
2/3x+
2/3)
综合运用
2、已知一次函数y=kx+b的图象是过A(0,-4),B(2,-3)两点的一条直线.
(1)求直线AB的解析式;
(2)将直线AB向左平移6个单位,求平移后的直线的解析式.
(3)将直线AB向上平移6个单位,求原点到平移后的直线的距离.
综合运用
学习目标
课堂小结
1.能够掌握直线平移的推导过程,体会不同情况下平移的移动规律。
2.能够灵活运用平移规律解决数学问题。
3.简单体会显性平移和隐性平移的区别。
(1)一次函数中两直线平行:k相等
(2)一次函数上下平移遵循:上加下减
(3)一次函数左右平移遵循:左加右减
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
