冀教版八年级数学下册22.3三角形的中位线课件(共20张PPT)
文档属性
| 名称 | 冀教版八年级数学下册22.3三角形的中位线课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
22.3三角形的中位线
冀教版数学八年级下册
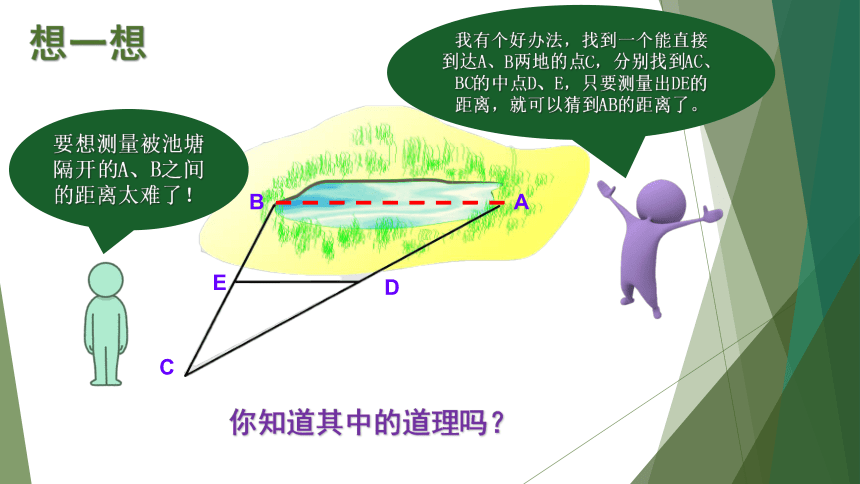
想一想
你知道其中的道理吗?
C
A
B
D
E
要想测量被池塘隔开的A、B之间的距离太难了!
我有个好办法,找到一个能直接到达A、B两地的点C,分别找到AC、BC的中点D、E,只要测量出DE的距离,就可以猜到AB的距离了。
三角形中位线定义
连结三角形两边中点的线段叫做三角形的中位线。
A
B
C
D
E
DE是△ABC的一条中位线。
边做边想
请折出三角形的中位线。
折出点D
折出点E
折出中位线DE
边做边想
请量出DE、BC的长度。
请量出∠ADB和∠B的度数。
猜想一下,中位线DE与BC有什么关系?
数量关系:DE等于BC的一半
位置关系:DE平行于BC
边做边想
沿ΔABC中位线DE剪开,ΔABC被分成了两部分,请把它们拼成一个四边形。
对比拼得的四边形与原三角形的位置关系,ΔADE经过怎样的图形变换就可以把三角形变成四边形。
拼得的四边形是平行四边形吗?你能说明理由吗?
左
右
小组探究
讨论证明
如图,DE是△ABC的中位线。求证:
A
B
C
D
E
F
提示:
我们可以通过添加辅助线构造出这个平行四边形吗?
小组探究
讨论证明
证明:
延长DE到F,使EF=DE,连接CF
∵DE=EF,AE=EC,
∠AED=∠CEF
∴△ADE≌△CFE
∴∠ADE=∠F,AD=CF
∴AB∥CF
又∵BD=AD=CF
∴四边形BCFD是平行四边形。
∴
A
B
C
D
E
F
同学们还有其他添加辅助线的方法吗?
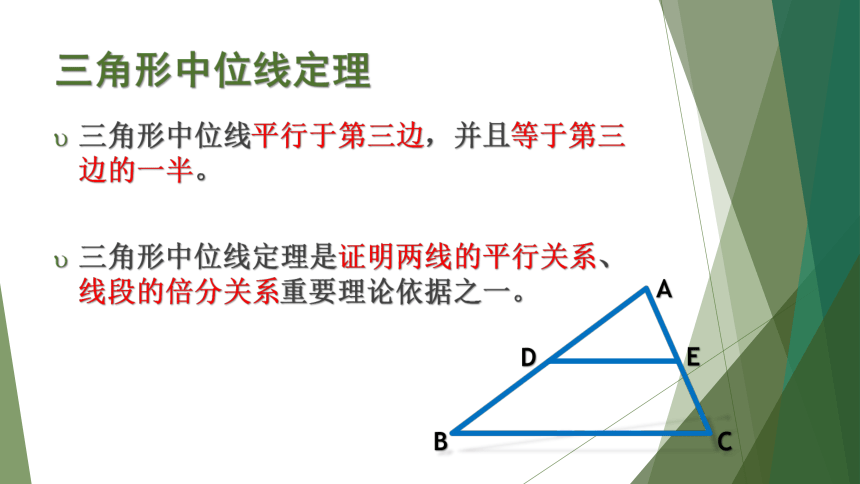
三角形中位线定理
三角形中位线平行于第三边,并且等于第三边的一半。
三角形中位线定理是证明两线的平行关系、线段的倍分关系重要理论依据之一。
A
B
C
D
E
延伸思考
三角形中位线和中线有什么区别?
中位线是两边中点的连线
中线是一个顶点和对边中点的连线
延伸思考
每个三角形有几条中位线?
图中的三角形有什么关系?
课堂练习
已知:点D、E、F分别是△ABC的三边AB、BC、AC的中点.
?
若AB=18cm,则EF=
cm;
?
若DF=5cm,则BC=
cm;
?
若∠ADF=50°,则∠B=
°
?
已知:三边AB、BC、AC分别为18、10、12,
△
DEF的周长为_______________
课堂练习
如图在?ABC中,D,E,F分别是AB,BC,
AC的中点,AC=12,BC=16,求四边形DECF的周长。
课堂练习
在四边形ABC中,AD=BC,P为对角线BD的中点,M为DC的中点,N为AB的中点。
求证:△PMN是等腰三角形。
课堂练习
在四边形ABC中,AD=BC,P为对角线BD的中点,M为DC的中点,N为AB的中点。
求证:△PMN是等腰三角形。
课堂小结
三角形中位线定义:连结三角形两边中点的线段叫做三角形的中位线。
三角形中位线定理:三角形中位线平行于第三边,并且等于第三边的一半。
通过图形旋转,把研究三角形中位线性质的转化成了研究平行四边形性质。
探索数学问题的常用的步骤:
观察——测量——猜想——证明
课后作业
必做题:
习题:第132页
A组:1、2;
B组:1
选做题:
△ABC的中线BD、CE交于点O,点F、G分别是OB、OC的中点。求证:四边形DEFG是平行四边形。
B
A
C
D
E
O
F
G
三角形向左旋转
三角形向右旋转
22.3三角形的中位线
冀教版数学八年级下册
想一想
你知道其中的道理吗?
C
A
B
D
E
要想测量被池塘隔开的A、B之间的距离太难了!
我有个好办法,找到一个能直接到达A、B两地的点C,分别找到AC、BC的中点D、E,只要测量出DE的距离,就可以猜到AB的距离了。
三角形中位线定义
连结三角形两边中点的线段叫做三角形的中位线。
A
B
C
D
E
DE是△ABC的一条中位线。
边做边想
请折出三角形的中位线。
折出点D
折出点E
折出中位线DE
边做边想
请量出DE、BC的长度。
请量出∠ADB和∠B的度数。
猜想一下,中位线DE与BC有什么关系?
数量关系:DE等于BC的一半
位置关系:DE平行于BC
边做边想
沿ΔABC中位线DE剪开,ΔABC被分成了两部分,请把它们拼成一个四边形。
对比拼得的四边形与原三角形的位置关系,ΔADE经过怎样的图形变换就可以把三角形变成四边形。
拼得的四边形是平行四边形吗?你能说明理由吗?
左
右
小组探究
讨论证明
如图,DE是△ABC的中位线。求证:
A
B
C
D
E
F
提示:
我们可以通过添加辅助线构造出这个平行四边形吗?
小组探究
讨论证明
证明:
延长DE到F,使EF=DE,连接CF
∵DE=EF,AE=EC,
∠AED=∠CEF
∴△ADE≌△CFE
∴∠ADE=∠F,AD=CF
∴AB∥CF
又∵BD=AD=CF
∴四边形BCFD是平行四边形。
∴
A
B
C
D
E
F
同学们还有其他添加辅助线的方法吗?
三角形中位线定理
三角形中位线平行于第三边,并且等于第三边的一半。
三角形中位线定理是证明两线的平行关系、线段的倍分关系重要理论依据之一。
A
B
C
D
E
延伸思考
三角形中位线和中线有什么区别?
中位线是两边中点的连线
中线是一个顶点和对边中点的连线
延伸思考
每个三角形有几条中位线?
图中的三角形有什么关系?
课堂练习
已知:点D、E、F分别是△ABC的三边AB、BC、AC的中点.
?
若AB=18cm,则EF=
cm;
?
若DF=5cm,则BC=
cm;
?
若∠ADF=50°,则∠B=
°
?
已知:三边AB、BC、AC分别为18、10、12,
△
DEF的周长为_______________
课堂练习
如图在?ABC中,D,E,F分别是AB,BC,
AC的中点,AC=12,BC=16,求四边形DECF的周长。
课堂练习
在四边形ABC中,AD=BC,P为对角线BD的中点,M为DC的中点,N为AB的中点。
求证:△PMN是等腰三角形。
课堂练习
在四边形ABC中,AD=BC,P为对角线BD的中点,M为DC的中点,N为AB的中点。
求证:△PMN是等腰三角形。
课堂小结
三角形中位线定义:连结三角形两边中点的线段叫做三角形的中位线。
三角形中位线定理:三角形中位线平行于第三边,并且等于第三边的一半。
通过图形旋转,把研究三角形中位线性质的转化成了研究平行四边形性质。
探索数学问题的常用的步骤:
观察——测量——猜想——证明
课后作业
必做题:
习题:第132页
A组:1、2;
B组:1
选做题:
△ABC的中线BD、CE交于点O,点F、G分别是OB、OC的中点。求证:四边形DEFG是平行四边形。
B
A
C
D
E
O
F
G
三角形向左旋转
三角形向右旋转
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
