苏科版七年级下册数学:12.1 定义与命题 课件(共29张PPT)
文档属性
| 名称 | 苏科版七年级下册数学:12.1 定义与命题 课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 13:37:20 | ||
图片预览








文档简介
(共29张PPT)
“数学,根本上是玩概念的!”
李邦河(1942—,中国科学院院士),浙江乐清(现乐清市)仙溪镇人.在雁荡中学度过了初中时代.1965年毕业于中国科学技术大学应用数学系,同年到中国科学院数学研究所工作,曾担任该所基础数学研究室主任,现任中国科学院数学与系统科学研究院研究员.2001年,他当选为中国科学院院士.
数学,根本上是玩概念的!
□
为什么要学习定义与命题
它是一种方程
它是一种两边都是整式的方程
它是只含有一个未知数且未知数的
最高项的次数是一次的整式方程
一元一次方程
□
为什么要学习定义与命题
在老师的描述中说出这是什么数学名词?
□
12.1
定义与命题
□
板块一
定义的意义
一般地,对某一名称或术语进行描述或作出
规定就叫做该名称或术语的定义.
□
板块一
定义的意义
你能说出下列名称的定义吗?
平行线:
绝对值:
方程的解:
在同一平面内,不相交的两条直线是平行线.
数轴上表示一个数的点到原点的距离是这个数的绝对值.
能使方程两边的值相等的未知数的值是方程的解.
(规定)
(描述)
(描述)
□
板块一
定义的作用
选_________,原因如下:
共同点:____________________________________
不同点:_________________________________________
由此把__________选项归为一类。,叫做“________”
定义为:“________________的_______叫做_______”
(1)选择下列式子中与众不同的一个
B
都是等式
B项不含字母,A、C、D项都含有字母
A、C、D
方程
含有字母
等式
方程
□
板块一
定义的作用
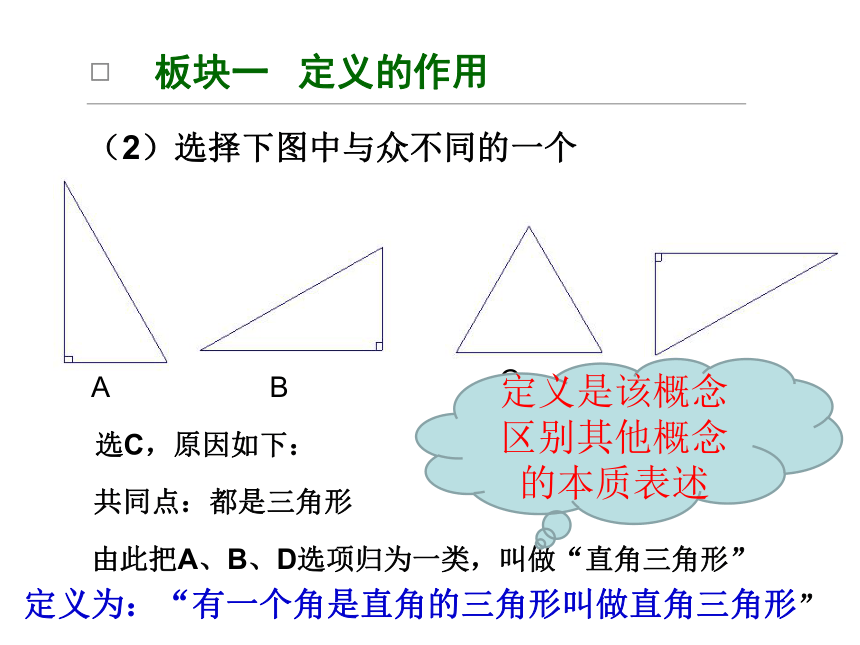
A
选C,原因如下:
共同点:都是三角形
由此把A、B、D选项归为一类,叫做“直角三角形”
定义为:“有一个角是直角的三角形叫做直角三角形”
B
C
D
(2)选择下图中与众不同的一个
定义是该概念区别其他概念的本质表述
□
板块一
定义的作用
(3)下列不互为相反数的是(
)
A.
3与-3
B.
-4与4
C.
a与-a
D.
-4与2
(4)若a、b
互为相反数,则a+b
=____.
定义既可当作判定,也可当作性质。
D
0
(5)判断
(
)
×
定义具有确定性。
□
板块一
定义的作用
定义是推理的依据
□
板块二
命题的意义
比较下列句子在表述形式上哪些对事情作了判断?哪些没有对事情作出判断?
(1)鸟是动物;
(2)若a2=4,求a的值;
(3)若a2=b2,则a=b;
(4)a、b两条直线平行吗?
(5)画一个角等于已知角;
(6)0.33是无理数;
(7)直角三角形两锐角互余.
每个句子都有一定的语调,表示陈述的陈述句、表示疑问的疑问句、表示祈使的祈使句、表示感叹的感叹句等
□
板块二
命题的意义
像(1)、(3)、(6)、(7),判断一件事情的句子叫做命题.
比较下列句子在表述形式上哪些对事情作了判断?哪些没有对事情作出判断?
(1)鸟是动物;
(3)若a2=b2,则a=b;
(6)0.33是无理数;
(7)两直线平行,同位角相等.
你认为判断是否是命题的关键是什么?
□
板块二
命题的意义
下列句子中,哪些是命题?哪些不是命题?
不是
不是
是
不是
是
(1)画三角形一边上的中线;
(2)a、b互为相反数吗?
(3)两直线平行,同位角相等;
(4)过一点画已知直线的垂线
(5)若a=b
,则a2=
b2
命题有哪些特点?
(6)同位角相等,两直线平行
是
□
板块二
命题的结构
命题:
两直线平行,同位角相等.
条件
结论
(题设)
在数学中,命题一般可看作由题设(条件)
和结论两部分组成,题设是已知事项,结论是
由已知事项推出的事项.
(结论)
□
板块二
命题的结构
相等
对顶角
(两个角是)
条件:
(补上适当词语)
结论:
角
两个
(1)对顶角相等
条件:两个角是对顶角,
结论:这两个角相等.
找出下列命题的条件和结论.
如果两个角是对顶角,那么这两个角相等.
改写:
方法:
先结论,
后条件.
□
板块二
命题的结构
找出下列命题的条件和结论.
(2)π是无理数
条件:一个数是π
,
结论:这个数是无理数.
如果一个数是π
,那么这个数是无理数.
改写:
□
板块二
命题的判断
下列命题的条件是什么?结论是什么?
1、如果a、b两数的积为0,那么a、b两数都为0
2、如果两个角互为补角,那么这两个角的和为1800
3、两直线平行,同旁内角互补
4、三角形内角和为1800
5、有公共顶点的两个角是对顶角
上述命题是否成立?
像这样,条件成立,结论也成立的命题叫做真命题
条件成立,结论不成立的命题叫做假命题
说明假命题的方法:
举反例
使之具有命题的条件,而不具有
命题的结论。
□
板块二
命题的判断
如何证实一个命题是真命题呢
想一想
真命题常常通过推理的方式(根据已知事实来推断未知事实)
也有一些命题是
人们经过长期实践后而公认为正确的命题
□
板块二
命题的判断
□
板块二
命题的判断
长期实践的认识--基本事实
三角形的内角和是1800。
说明真命题的方法:
证明
□
板块二
命题的判断
他的方法是:
确定一些公认的命题作为基本事实
用推理的方法证实其它命题的正确性
推理的过程叫证明
经过证明的真命题叫定理
欧几里得(Euclid)是古希腊著名数学家、欧氏几何学开创者
有关概念、公理
条件1
定理1
有关概念、公理
条件2
定理2
定理3
……
……
《原本》问世之前,世界上还没有一本数学书籍像《原本》这样编排,因此《原本》是一部具有划时代意义的著作。
□
板块二
命题的作用
□
板块二
命题的作用
三角形的内角和是1800,已经经过证明,是正确的,以后就作为说理证明的依据直接使用。
□
板块二
命题的判断
(1)两直线平行
(2)两数相等
(3)对顶角
(4)同位角相等
(8)两数的平方相等
(6)两角相等
(7)等边三角形
(5)三边相等
请用这八张卡片作为命题的条件和结论,
你能组成几个真命题?
□
板块三
定义与命题的区别与联系
定义不等同命题,只是有的时候定义可以认为是命题。
定义是真命题,但命题不一定是定义。
真命题
定义
回顾下你本节课的学习,提出一个问题.(可以是收获,发现,温馨提醒,困惑等)
□
板块四
提出问题
□
板块五
研究复杂问题的一般思路
(1)阅读:课本p144等相关内容
(2)必做:习题12.1
1,2
(3)选做:撰写感悟小文章
□
作业布置
□
欢迎批评指正
“数学,根本上是玩概念的!”
李邦河(1942—,中国科学院院士),浙江乐清(现乐清市)仙溪镇人.在雁荡中学度过了初中时代.1965年毕业于中国科学技术大学应用数学系,同年到中国科学院数学研究所工作,曾担任该所基础数学研究室主任,现任中国科学院数学与系统科学研究院研究员.2001年,他当选为中国科学院院士.
数学,根本上是玩概念的!
□
为什么要学习定义与命题
它是一种方程
它是一种两边都是整式的方程
它是只含有一个未知数且未知数的
最高项的次数是一次的整式方程
一元一次方程
□
为什么要学习定义与命题
在老师的描述中说出这是什么数学名词?
□
12.1
定义与命题
□
板块一
定义的意义
一般地,对某一名称或术语进行描述或作出
规定就叫做该名称或术语的定义.
□
板块一
定义的意义
你能说出下列名称的定义吗?
平行线:
绝对值:
方程的解:
在同一平面内,不相交的两条直线是平行线.
数轴上表示一个数的点到原点的距离是这个数的绝对值.
能使方程两边的值相等的未知数的值是方程的解.
(规定)
(描述)
(描述)
□
板块一
定义的作用
选_________,原因如下:
共同点:____________________________________
不同点:_________________________________________
由此把__________选项归为一类。,叫做“________”
定义为:“________________的_______叫做_______”
(1)选择下列式子中与众不同的一个
B
都是等式
B项不含字母,A、C、D项都含有字母
A、C、D
方程
含有字母
等式
方程
□
板块一
定义的作用
A
选C,原因如下:
共同点:都是三角形
由此把A、B、D选项归为一类,叫做“直角三角形”
定义为:“有一个角是直角的三角形叫做直角三角形”
B
C
D
(2)选择下图中与众不同的一个
定义是该概念区别其他概念的本质表述
□
板块一
定义的作用
(3)下列不互为相反数的是(
)
A.
3与-3
B.
-4与4
C.
a与-a
D.
-4与2
(4)若a、b
互为相反数,则a+b
=____.
定义既可当作判定,也可当作性质。
D
0
(5)判断
(
)
×
定义具有确定性。
□
板块一
定义的作用
定义是推理的依据
□
板块二
命题的意义
比较下列句子在表述形式上哪些对事情作了判断?哪些没有对事情作出判断?
(1)鸟是动物;
(2)若a2=4,求a的值;
(3)若a2=b2,则a=b;
(4)a、b两条直线平行吗?
(5)画一个角等于已知角;
(6)0.33是无理数;
(7)直角三角形两锐角互余.
每个句子都有一定的语调,表示陈述的陈述句、表示疑问的疑问句、表示祈使的祈使句、表示感叹的感叹句等
□
板块二
命题的意义
像(1)、(3)、(6)、(7),判断一件事情的句子叫做命题.
比较下列句子在表述形式上哪些对事情作了判断?哪些没有对事情作出判断?
(1)鸟是动物;
(3)若a2=b2,则a=b;
(6)0.33是无理数;
(7)两直线平行,同位角相等.
你认为判断是否是命题的关键是什么?
□
板块二
命题的意义
下列句子中,哪些是命题?哪些不是命题?
不是
不是
是
不是
是
(1)画三角形一边上的中线;
(2)a、b互为相反数吗?
(3)两直线平行,同位角相等;
(4)过一点画已知直线的垂线
(5)若a=b
,则a2=
b2
命题有哪些特点?
(6)同位角相等,两直线平行
是
□
板块二
命题的结构
命题:
两直线平行,同位角相等.
条件
结论
(题设)
在数学中,命题一般可看作由题设(条件)
和结论两部分组成,题设是已知事项,结论是
由已知事项推出的事项.
(结论)
□
板块二
命题的结构
相等
对顶角
(两个角是)
条件:
(补上适当词语)
结论:
角
两个
(1)对顶角相等
条件:两个角是对顶角,
结论:这两个角相等.
找出下列命题的条件和结论.
如果两个角是对顶角,那么这两个角相等.
改写:
方法:
先结论,
后条件.
□
板块二
命题的结构
找出下列命题的条件和结论.
(2)π是无理数
条件:一个数是π
,
结论:这个数是无理数.
如果一个数是π
,那么这个数是无理数.
改写:
□
板块二
命题的判断
下列命题的条件是什么?结论是什么?
1、如果a、b两数的积为0,那么a、b两数都为0
2、如果两个角互为补角,那么这两个角的和为1800
3、两直线平行,同旁内角互补
4、三角形内角和为1800
5、有公共顶点的两个角是对顶角
上述命题是否成立?
像这样,条件成立,结论也成立的命题叫做真命题
条件成立,结论不成立的命题叫做假命题
说明假命题的方法:
举反例
使之具有命题的条件,而不具有
命题的结论。
□
板块二
命题的判断
如何证实一个命题是真命题呢
想一想
真命题常常通过推理的方式(根据已知事实来推断未知事实)
也有一些命题是
人们经过长期实践后而公认为正确的命题
□
板块二
命题的判断
□
板块二
命题的判断
长期实践的认识--基本事实
三角形的内角和是1800。
说明真命题的方法:
证明
□
板块二
命题的判断
他的方法是:
确定一些公认的命题作为基本事实
用推理的方法证实其它命题的正确性
推理的过程叫证明
经过证明的真命题叫定理
欧几里得(Euclid)是古希腊著名数学家、欧氏几何学开创者
有关概念、公理
条件1
定理1
有关概念、公理
条件2
定理2
定理3
……
……
《原本》问世之前,世界上还没有一本数学书籍像《原本》这样编排,因此《原本》是一部具有划时代意义的著作。
□
板块二
命题的作用
□
板块二
命题的作用
三角形的内角和是1800,已经经过证明,是正确的,以后就作为说理证明的依据直接使用。
□
板块二
命题的判断
(1)两直线平行
(2)两数相等
(3)对顶角
(4)同位角相等
(8)两数的平方相等
(6)两角相等
(7)等边三角形
(5)三边相等
请用这八张卡片作为命题的条件和结论,
你能组成几个真命题?
□
板块三
定义与命题的区别与联系
定义不等同命题,只是有的时候定义可以认为是命题。
定义是真命题,但命题不一定是定义。
真命题
定义
回顾下你本节课的学习,提出一个问题.(可以是收获,发现,温馨提醒,困惑等)
□
板块四
提出问题
□
板块五
研究复杂问题的一般思路
(1)阅读:课本p144等相关内容
(2)必做:习题12.1
1,2
(3)选做:撰写感悟小文章
□
作业布置
□
欢迎批评指正
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
