北师大版八年级下册数学 第六章 平行四边形复习 课件(共18张PPT)
文档属性
| 名称 | 北师大版八年级下册数学 第六章 平行四边形复习 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-09 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
回顾梳理
(1)
平行四边形的两组对边分别平行且相等.
(2)
平行四边形的对角相等.
(3)
平行四边形的对角线互相平分.
平行四边形有哪些性质?
平行四边形有哪些判定方法?
(1)
两组对边分别平行的四边形是平行四边形.
(2)
一组对边平行且相等的四边形是平行四边形.
(3)
两组对边分别相等的四边形是平行四边形.
(4)
对角线互相平分的四边形是平行四边形.
(5)
两组对角分别相等的四边形是平行四边形.
学以致用
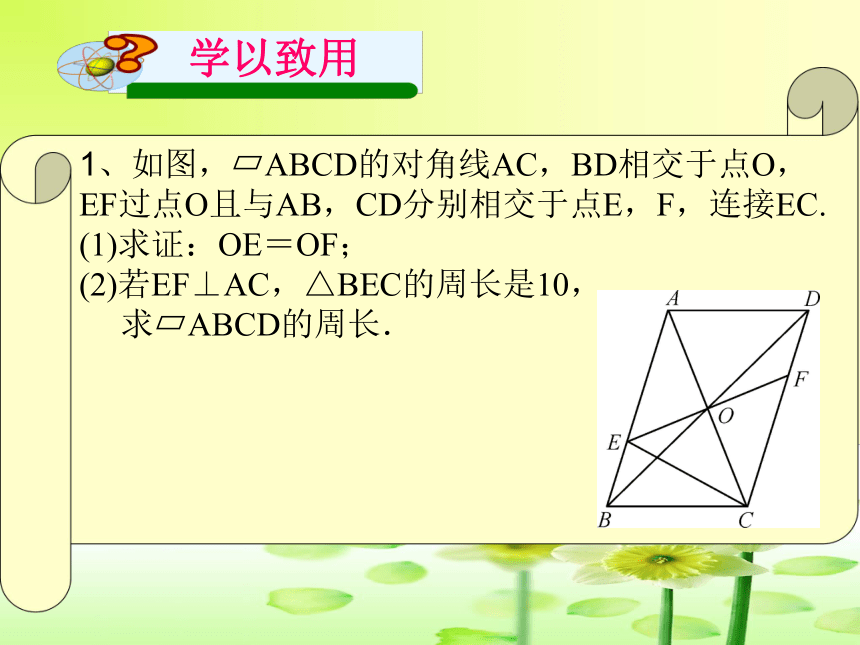
1、如图,?ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,
求?ABCD的周长.
学以致用
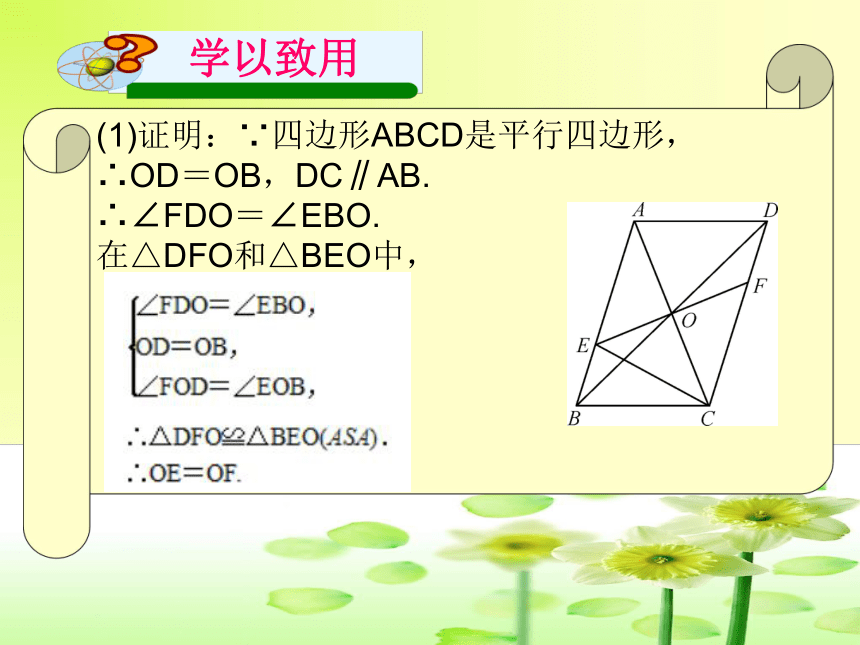
(1)证明:∵四边形ABCD是平行四边形,
∴OD=OB,DC∥AB.
∴∠FDO=∠EBO.
在△DFO和△BEO中,
学以致用
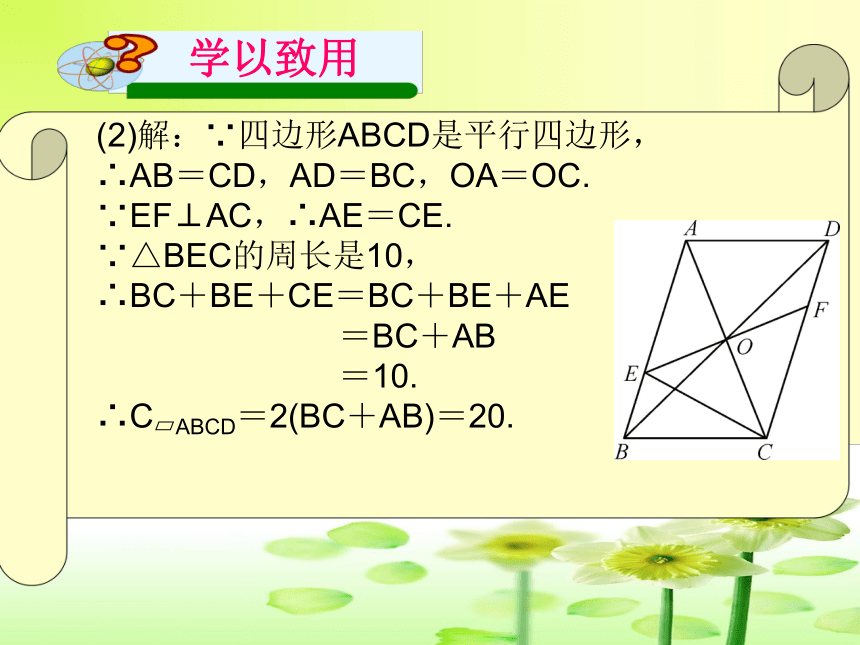
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC.
∵EF⊥AC,∴AE=CE.
∵△BEC的周长是10,
∴BC+BE+CE=BC+BE+AE
=BC+AB
=10.
∴C?ABCD=2(BC+AB)=20.
学以致用
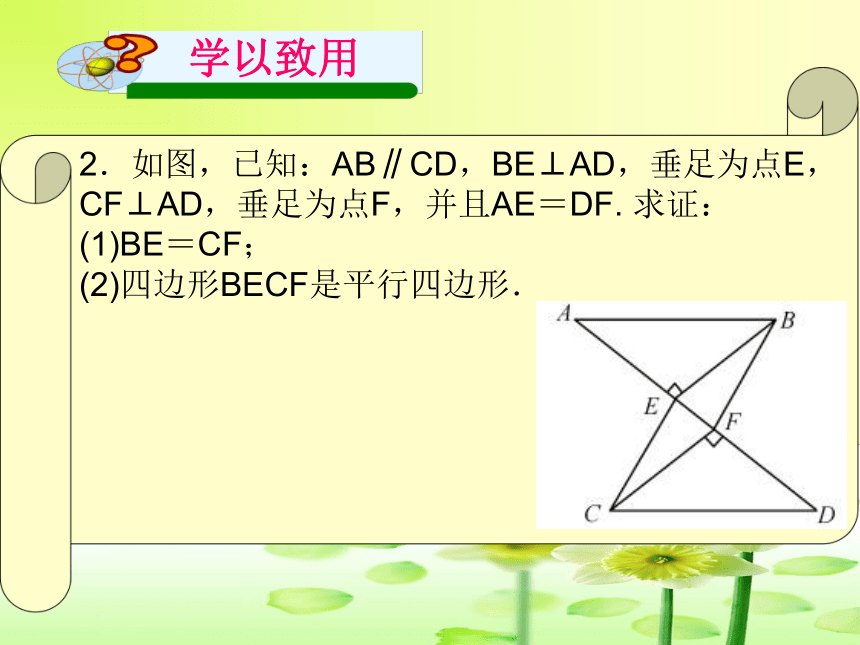
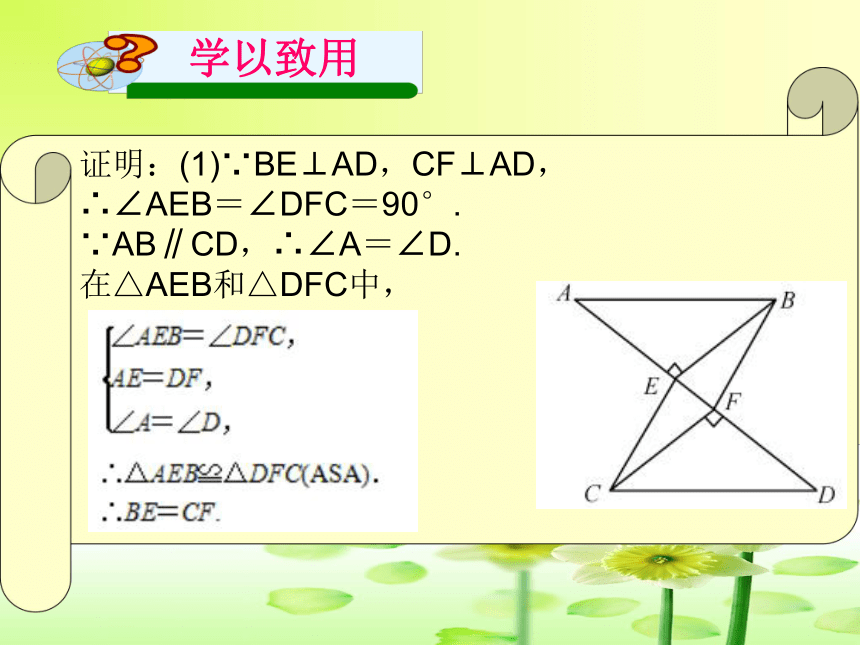
2.如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:
(1)BE=CF;
(2)四边形BECF是平行四边形.
学以致用
证明:(1)∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°.
∵AB∥CD,∴∠A=∠D.
在△AEB和△DFC中,
学以致用
(2)∵BE⊥AD,CF⊥AD,
∴BE∥CF.
又∵BE=CF,
∴四边形BECF是平行四边形.
在
ABCD中,
∠A:∠B=3:6,
则∠C=
度.
2.
在?ABCD中,两邻边的差为4
cm,
周长为32
cm,则两邻边长分别
为
cm,
cm.
小试牛刀
60
10
6
3.如图,在?ABCD中,AB=4,BC=6,
AC的垂直平分线交AD于点E,
则△CDE的周长是(
)
A.7
B.10
C.11
D.12
小试牛刀
B
4.如图:
在
ABCD中,
∠DAB的平分线
AE交CD于点E,
BC=9,AB=15,
则
CE=
.
A
B
C
D
E
1
2
3
6
初露锋芒
9
15
9
15
9
6
5.
如图:
平行四边形ABCD中,
AC、BD相交于点O,
AB=8,
△AOB的面积为
,
ABCD的面积为
.
A
B
C
D
O
24
24
96
8
6
10
4,
12
B.
6,
8
C.
8,
26
D.
12,
20
则以下列两条线段长为对角线的长,
能组成平行四边形的是(
)
D
AC=12,
BD=20.则△AOB的周长为
再展雄姿
2
6
3
4
4
13
已知:
ABCD中,直线MN//AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。
☆找平行四边形
如图,在
ABCD中,E、F、G、H
分别是各边上的点,且AE=CF,BG=DH。
求证:EF与GH互相平分。
A
B
C
D
H
E
G
F
☆构造平行四边形
6.如图,在?ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD的中点,求证:四边形AECF是平行四边形.
我也会做
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵点E,F分别是OB,OD的中点,
∴OE=1/2OB,OF=1/2
OD.
∴OE=OF.
又∵OA=OC,
∴四边形AECF是平行四边形.
合作探究
7、如图,?ABCD
中,点O
是对角线AC
的中点,EF
过点O,与AD,BC
分别相交于点E,F,GH
过点O,与AB,CD
分别相交于点G,H,连接EG,FG,FH,EH.求证:四边形EGFH
是平行四边形.
证明:∵四边形ABCD
为平行四边形,
∴AD∥BC.
∴∠EAO=∠FCO.
∵O为AC的中点,
∴OA=OC.
在△OAE和△OCF中,
∵∠EAO=∠FCO,
OA=OC
∠AOE=∠COF
∴△OAE≌△OCF(ASA).
∴OE=OF.
同理可证得OG=OH.
∴四边形EGFH是平行四边形.
□ABCD的周长为32cm,
∠ABC的角平分线交边AD所在直线于点E,且AE:ED
=3:2,则AB=______________.
6cm或12cm
3x
3x
2x
x
2x
3x
通过这节课的复习,
你又增加了哪些收获?
能与大家一起分享吗?
丰
收
园
回顾梳理
(1)
平行四边形的两组对边分别平行且相等.
(2)
平行四边形的对角相等.
(3)
平行四边形的对角线互相平分.
平行四边形有哪些性质?
平行四边形有哪些判定方法?
(1)
两组对边分别平行的四边形是平行四边形.
(2)
一组对边平行且相等的四边形是平行四边形.
(3)
两组对边分别相等的四边形是平行四边形.
(4)
对角线互相平分的四边形是平行四边形.
(5)
两组对角分别相等的四边形是平行四边形.
学以致用
1、如图,?ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,△BEC的周长是10,
求?ABCD的周长.
学以致用
(1)证明:∵四边形ABCD是平行四边形,
∴OD=OB,DC∥AB.
∴∠FDO=∠EBO.
在△DFO和△BEO中,
学以致用
(2)解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC.
∵EF⊥AC,∴AE=CE.
∵△BEC的周长是10,
∴BC+BE+CE=BC+BE+AE
=BC+AB
=10.
∴C?ABCD=2(BC+AB)=20.
学以致用
2.如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:
(1)BE=CF;
(2)四边形BECF是平行四边形.
学以致用
证明:(1)∵BE⊥AD,CF⊥AD,
∴∠AEB=∠DFC=90°.
∵AB∥CD,∴∠A=∠D.
在△AEB和△DFC中,
学以致用
(2)∵BE⊥AD,CF⊥AD,
∴BE∥CF.
又∵BE=CF,
∴四边形BECF是平行四边形.
在
ABCD中,
∠A:∠B=3:6,
则∠C=
度.
2.
在?ABCD中,两邻边的差为4
cm,
周长为32
cm,则两邻边长分别
为
cm,
cm.
小试牛刀
60
10
6
3.如图,在?ABCD中,AB=4,BC=6,
AC的垂直平分线交AD于点E,
则△CDE的周长是(
)
A.7
B.10
C.11
D.12
小试牛刀
B
4.如图:
在
ABCD中,
∠DAB的平分线
AE交CD于点E,
BC=9,AB=15,
则
CE=
.
A
B
C
D
E
1
2
3
6
初露锋芒
9
15
9
15
9
6
5.
如图:
平行四边形ABCD中,
AC、BD相交于点O,
AB=8,
△AOB的面积为
,
ABCD的面积为
.
A
B
C
D
O
24
24
96
8
6
10
4,
12
B.
6,
8
C.
8,
26
D.
12,
20
则以下列两条线段长为对角线的长,
能组成平行四边形的是(
)
D
AC=12,
BD=20.则△AOB的周长为
再展雄姿
2
6
3
4
4
13
已知:
ABCD中,直线MN//AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。
☆找平行四边形
如图,在
ABCD中,E、F、G、H
分别是各边上的点,且AE=CF,BG=DH。
求证:EF与GH互相平分。
A
B
C
D
H
E
G
F
☆构造平行四边形
6.如图,在?ABCD中,对角线AC,BD相交于点O,点E,F分别是OB,OD的中点,求证:四边形AECF是平行四边形.
我也会做
证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵点E,F分别是OB,OD的中点,
∴OE=1/2OB,OF=1/2
OD.
∴OE=OF.
又∵OA=OC,
∴四边形AECF是平行四边形.
合作探究
7、如图,?ABCD
中,点O
是对角线AC
的中点,EF
过点O,与AD,BC
分别相交于点E,F,GH
过点O,与AB,CD
分别相交于点G,H,连接EG,FG,FH,EH.求证:四边形EGFH
是平行四边形.
证明:∵四边形ABCD
为平行四边形,
∴AD∥BC.
∴∠EAO=∠FCO.
∵O为AC的中点,
∴OA=OC.
在△OAE和△OCF中,
∵∠EAO=∠FCO,
OA=OC
∠AOE=∠COF
∴△OAE≌△OCF(ASA).
∴OE=OF.
同理可证得OG=OH.
∴四边形EGFH是平行四边形.
□ABCD的周长为32cm,
∠ABC的角平分线交边AD所在直线于点E,且AE:ED
=3:2,则AB=______________.
6cm或12cm
3x
3x
2x
x
2x
3x
通过这节课的复习,
你又增加了哪些收获?
能与大家一起分享吗?
丰
收
园
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
