湘教版八年级下册数学:4.4 用待定系数法确定一次函数表达式(第1课时)课件 (共16张PPT)
文档属性
| 名称 | 湘教版八年级下册数学:4.4 用待定系数法确定一次函数表达式(第1课时)课件 (共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 17:03:48 | ||
图片预览





文档简介
(共16张PPT)
(第1课时)
用待定系数法确定
一次函数表达式
学习目标
1.知识与技能:根据函数的图像确定一次函数的表达式,会运用一次函数的思想解决实际问题;
2.过程与方法:让学生经历观察、操作、合作、探究、交流、推理等活动,体会数学的建模、数形结合思想,进一步发展推理能力及有条理表达能力;
3.情感态度与价值观:使学生经历探索、合作、交流的学习过程,激发学生对数学的兴趣,获得成功的体验.
重点难点
1.重点:根据所给信息确定一次函数的表达式;
2.难点:体会数学的建模、数形结合思想.
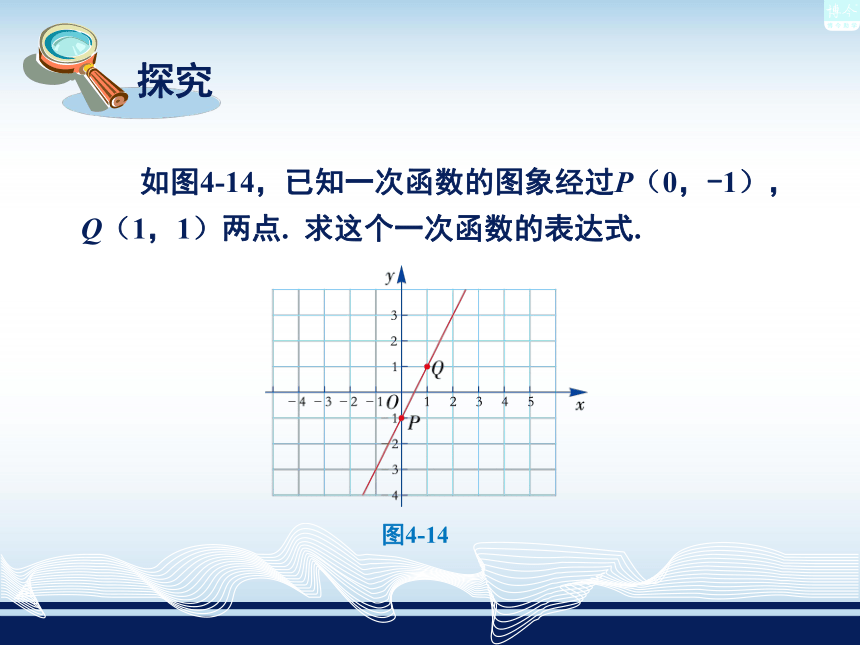
如图4-14,已知一次函数的图象经过P(0,-1),
Q(1,1)两点.
求这个一次函数的表达式.
图4-14
解:设y=kx+b
,将(0,-1),(1,1)代入得
所以,这个一次函数的表达式为y
=
2x-
1.
因此摄氏温度与华氏温度的函数关系式为
所以
y
=
-5x
+
40.
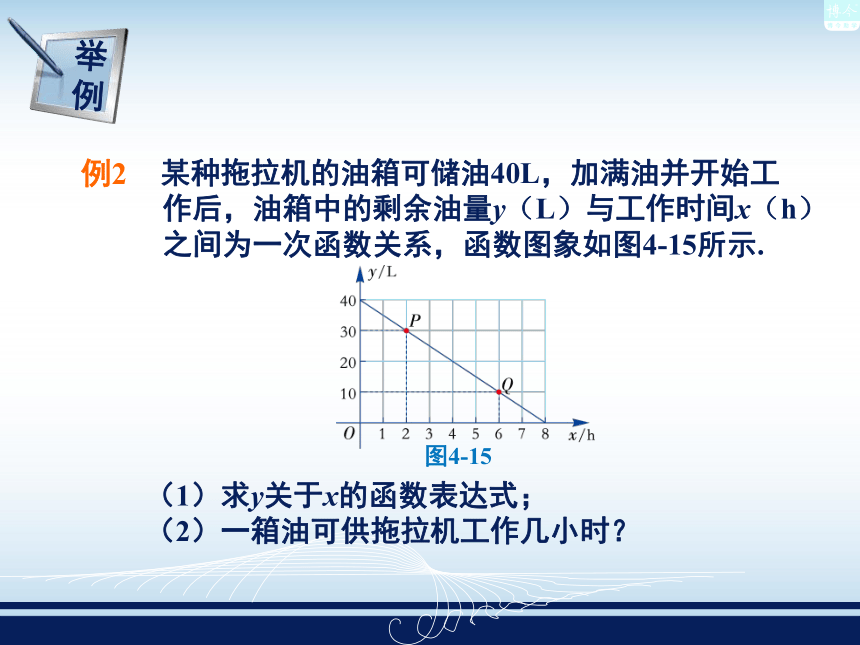
(1)求y关于x的函数表达式;
(2)解
当剩余油量为0时,
即y=0
时,
有
-5x
+
40
=
0,
解得
x
=
8.
所以一箱油可供拖拉机工作8
h.
(2)一箱油可供拖拉机工作几小时?
例3:已知:y-1与x-2成正比例,且当x=1,y=3时,求y与x的函数关系式。
解:设y-1=k(x-2),将x=1,y=3代入得
2=k(1-2)
2=-k
k=-2
故
y=-2(x-2)
即
y=-2x+4
1.
把温度84华氏度换算成摄氏温度.
2.
已知一次函数的图象经过两点A(-1,3),B(2,-5),求这个函数的解析式.
例
百舸竞渡,激情飞扬,端午节期间,某地举行龙舟比赛.甲、乙两支龙舟队在比赛时路程y(米)与时间x(分)之间的函数图象如图.根据图象回答下列问题:
(1)1.8分钟时,哪支龙舟队处于领先位置?
(2)在这次龙舟赛中,哪支龙舟队先到达终点?提前多
少时间到达?
(3)求乙队加速后,路程y(米)与时间x(分)之间的函数
关系式.
作业布置
P131页
A组
第1、2题;
P132页
B组
第4题.
再见
谢谢观看!欢迎指导!
(第1课时)
用待定系数法确定
一次函数表达式
学习目标
1.知识与技能:根据函数的图像确定一次函数的表达式,会运用一次函数的思想解决实际问题;
2.过程与方法:让学生经历观察、操作、合作、探究、交流、推理等活动,体会数学的建模、数形结合思想,进一步发展推理能力及有条理表达能力;
3.情感态度与价值观:使学生经历探索、合作、交流的学习过程,激发学生对数学的兴趣,获得成功的体验.
重点难点
1.重点:根据所给信息确定一次函数的表达式;
2.难点:体会数学的建模、数形结合思想.
如图4-14,已知一次函数的图象经过P(0,-1),
Q(1,1)两点.
求这个一次函数的表达式.
图4-14
解:设y=kx+b
,将(0,-1),(1,1)代入得
所以,这个一次函数的表达式为y
=
2x-
1.
因此摄氏温度与华氏温度的函数关系式为
所以
y
=
-5x
+
40.
(1)求y关于x的函数表达式;
(2)解
当剩余油量为0时,
即y=0
时,
有
-5x
+
40
=
0,
解得
x
=
8.
所以一箱油可供拖拉机工作8
h.
(2)一箱油可供拖拉机工作几小时?
例3:已知:y-1与x-2成正比例,且当x=1,y=3时,求y与x的函数关系式。
解:设y-1=k(x-2),将x=1,y=3代入得
2=k(1-2)
2=-k
k=-2
故
y=-2(x-2)
即
y=-2x+4
1.
把温度84华氏度换算成摄氏温度.
2.
已知一次函数的图象经过两点A(-1,3),B(2,-5),求这个函数的解析式.
例
百舸竞渡,激情飞扬,端午节期间,某地举行龙舟比赛.甲、乙两支龙舟队在比赛时路程y(米)与时间x(分)之间的函数图象如图.根据图象回答下列问题:
(1)1.8分钟时,哪支龙舟队处于领先位置?
(2)在这次龙舟赛中,哪支龙舟队先到达终点?提前多
少时间到达?
(3)求乙队加速后,路程y(米)与时间x(分)之间的函数
关系式.
作业布置
P131页
A组
第1、2题;
P132页
B组
第4题.
再见
谢谢观看!欢迎指导!
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
