人教版八年级下册数学18.1.2 平行四边形的判定(第一课时)课件 (共16张PPT)
文档属性
| 名称 | 人教版八年级下册数学18.1.2 平行四边形的判定(第一课时)课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 23:16:17 | ||
图片预览

文档简介
(共16张PPT)
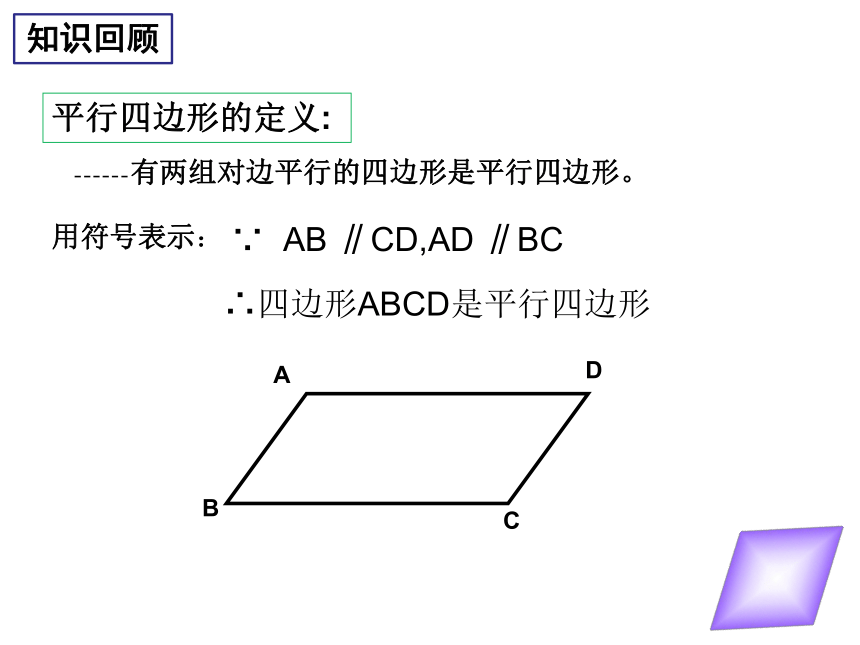
知识回顾
平行四边形的定义:
------
有两组对边平行的四边形是平行四边形。
用符号表示:
∵
AB
∥CD,AD
∥BC
∴四边形ABCD是平行四边形
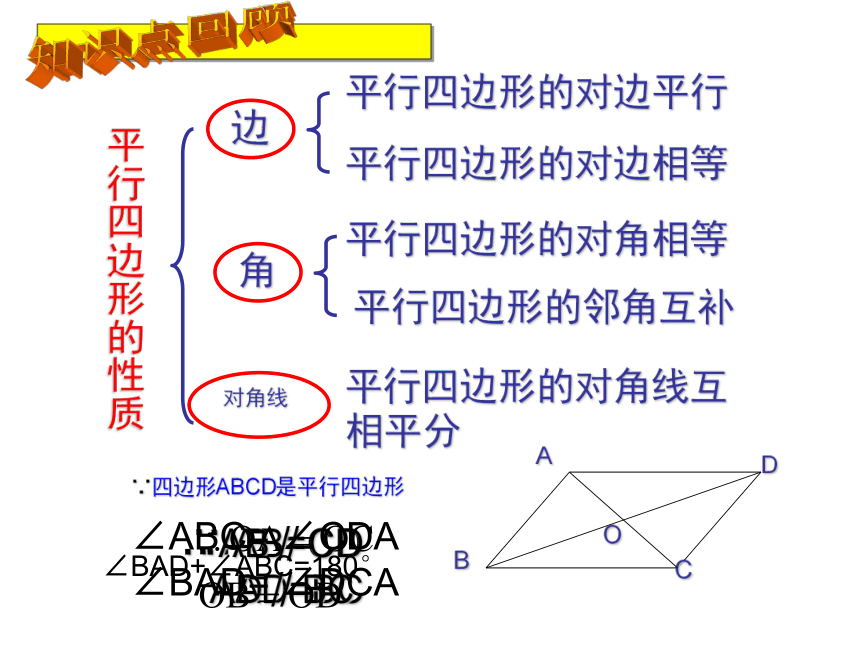
平行四边形的对边平行
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
∵四边形ABCD是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
平行四边形的性质
∠ABC=
∠CDA
∠BAD=
∠DCA
∠BAD+∠ABC=180°
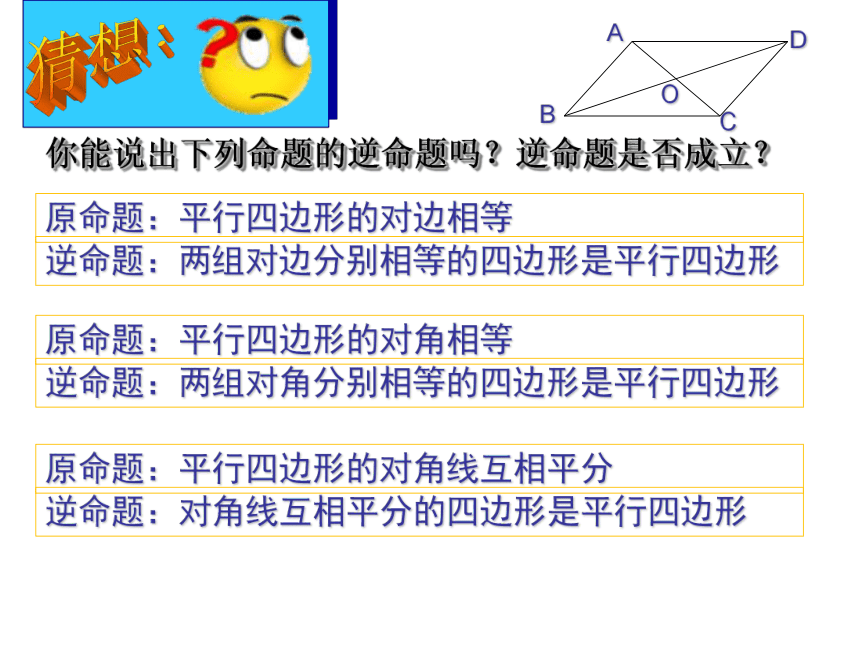
你能说出下列命题的逆命题吗?逆命题是否成立?
原命题:平行四边形的对边相等
原命题:平行四边形的对角线互相平分
逆命题:两组对边分别相等的四边形是平行四边形
原命题:平行四边形的对角相等
逆命题:两组对角分别相等的四边形是平行四边形
逆命题:对角线互相平分的四边形是平行四边形
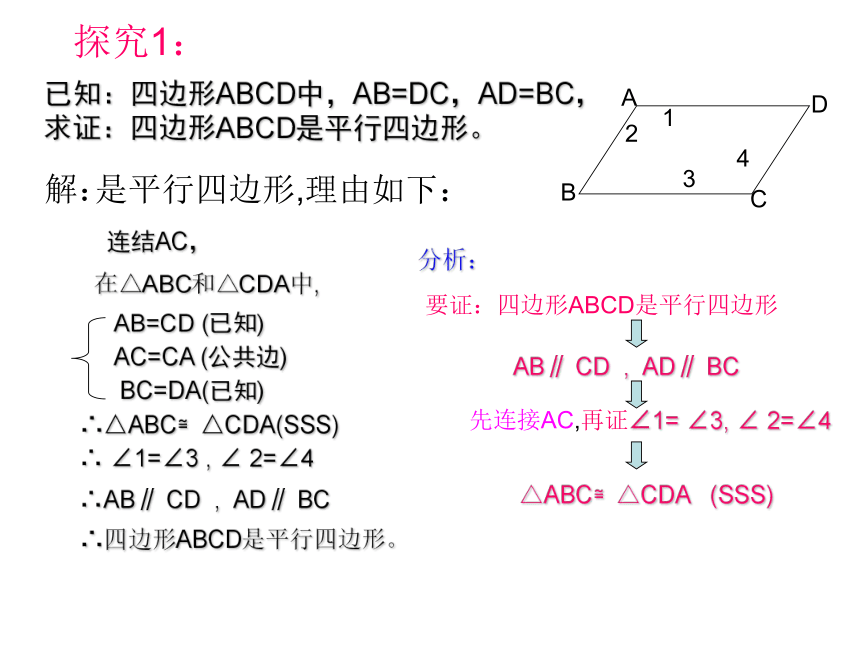
探究1:
已知:四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形。
分析:
要证:四边形ABCD是平行四边形
AB∥
CD
,
AD∥
BC
先连接AC,再证∠1=
∠3,
∠
2=∠4
△ABC≌△CDA
(SSS)
解:
是平行四边形,理由如下:
连结AC,
AB=CD
(已知)
AC=CA
(公共边)
BC=DA(已知)
∴△ABC≌△CDA(SSS)
在△ABC和△CDA中,
∴
∠1=∠3
,
∠
2=∠4
∴AB∥
CD
,
AD∥
BC
∴四边形ABCD是平行四边形。
1
2
3
4
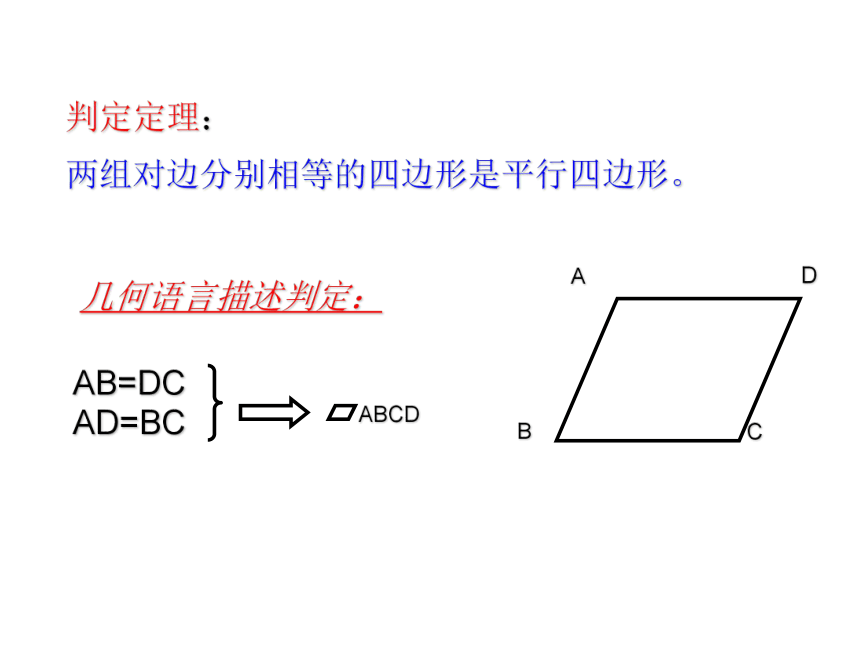
判定定理:
两组对边分别相等的四边形是平行四边形。
几何语言描述判定:
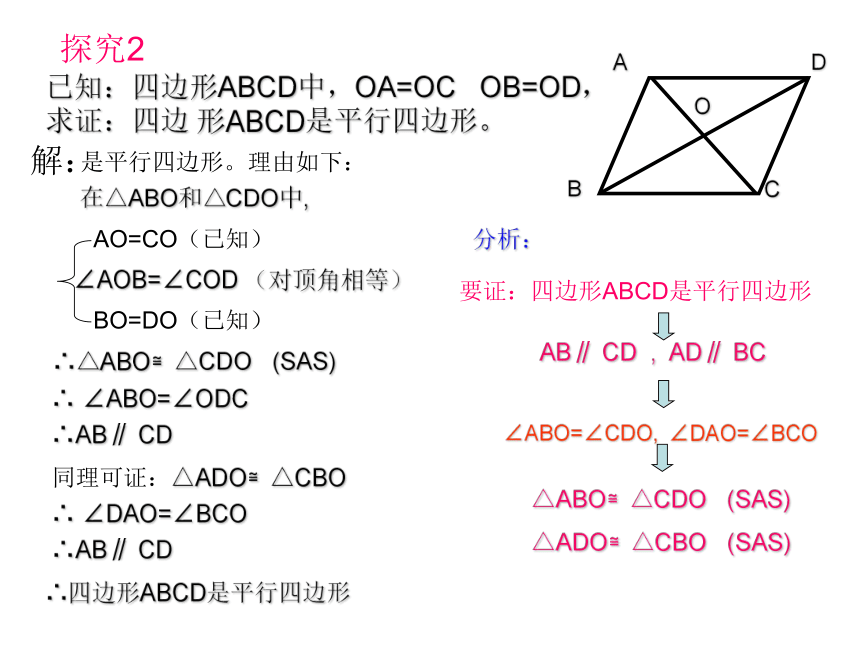
探究2
已知:四边形ABCD中,OA=OC
OB=OD,
求证:四边
形ABCD是平行四边形。
分析:
AB∥
CD
,
AD∥
BC
要证:四边形ABCD是平行四边形
解:
是平行四边形。理由如下:
在△ABO和△CDO中,
AO=CO(已知)
∠AOB=∠COD
(对顶角相等)
BO=DO(已知)
∴△ABO≌△CDO
(SAS)
∴
∠ABO=∠ODC
∴AB∥
CD
∴四边形ABCD是平行四边形
同理可证:△ADO≌△CBO
∴
∠DAO=∠BCO
∴AB∥
CD
对角线互相平分的四边形是平行四边形。
几何语言描述判定:
AO=CO
BO=DO
判定定理:
思考:如图,已知四边形ADCB中,
∠A=
∠c,
∠B=
∠D,那么四边形ABCD是平行四边形吗?
几何语言描述判定:
两组对角分别相等的四边形是平行四边形
判定定理:
∠A=
∠c
∠B=
∠D
ABCD
探究3
已知:四边形ABCD中,AB=CD,
AB∥CD
试问:四边
形ABCD是平行四边形吗?请说明理由。
B
解:
连接AC
A
C
D
1
2
是平行四边形,理由如下:
∵
AB∥
CD
∴
∠BAC=∠ACD
在△ABC和△CDA中,
AB=CD
(已知)
∠BAC=∠ACD
(已证)
AC=CA
(公共边)
∴△ABC≌△CDA
(SAS)
∴
∠1=∠2
∴
AD∥
BC
又∵
AB∥
CD
∴四边形ABCD是平行四边形
判定定理:
一组对边平行且相等的四边形是平行四边形。
几何语言描述判定:
ABCD
AD
BC
例:已知平行四边形ABCD中,E.F分别是边AD
BC的中点,求证:EB=DF
证明:∵四边形ABCD是平行四边形
∴AD∥BC
AD=BC
∵
DE=1/2AD
BF=1/2BC
∴DE∥BF
DE=BF
∴四边形EBFD是平行四边形
∴EB=DF
课堂练习:
如图,在四边形ABCD中,
①如果AD=8cm,AB=4cm,且BC=___cm,CD=____cm,那么四边形ABCD是平行四边形。
②∠A=1200,则∠B=____0,∠C=____0,∠D=____0时,四边形ABCD是平行四边形。
③如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。
8
4
点评:两组对边相等的四边形是平行四边形
60
120
60
点评:两组对角相等的四边形是平行四边形
6
点评:一组对边平行且相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
两组邻角分别互补的四边形是平行四边形
对角线互相平分的四边形是平行四边形
∴四边形ABCD是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
∠ABC=
∠CDA
∠BAD=
∠DCA
∠BAD+∠ABC=180°
∠BCD+∠ABC=180°
归纳小结
一组对边平行且相等的四边形是平行四边形
平行四边形的判定
作业布置
一、第47页练习:
1、2、4题
二、证明两组对角分别相等的四边形是平行四边形。
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
再
见
知识回顾
平行四边形的定义:
------
有两组对边平行的四边形是平行四边形。
用符号表示:
∵
AB
∥CD,AD
∥BC
∴四边形ABCD是平行四边形
平行四边形的对边平行
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
平行四边形的对角线互相平分
∵四边形ABCD是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
平行四边形的性质
∠ABC=
∠CDA
∠BAD=
∠DCA
∠BAD+∠ABC=180°
你能说出下列命题的逆命题吗?逆命题是否成立?
原命题:平行四边形的对边相等
原命题:平行四边形的对角线互相平分
逆命题:两组对边分别相等的四边形是平行四边形
原命题:平行四边形的对角相等
逆命题:两组对角分别相等的四边形是平行四边形
逆命题:对角线互相平分的四边形是平行四边形
探究1:
已知:四边形ABCD中,AB=DC,AD=BC,求证:四边形ABCD是平行四边形。
分析:
要证:四边形ABCD是平行四边形
AB∥
CD
,
AD∥
BC
先连接AC,再证∠1=
∠3,
∠
2=∠4
△ABC≌△CDA
(SSS)
解:
是平行四边形,理由如下:
连结AC,
AB=CD
(已知)
AC=CA
(公共边)
BC=DA(已知)
∴△ABC≌△CDA(SSS)
在△ABC和△CDA中,
∴
∠1=∠3
,
∠
2=∠4
∴AB∥
CD
,
AD∥
BC
∴四边形ABCD是平行四边形。
1
2
3
4
判定定理:
两组对边分别相等的四边形是平行四边形。
几何语言描述判定:
探究2
已知:四边形ABCD中,OA=OC
OB=OD,
求证:四边
形ABCD是平行四边形。
分析:
AB∥
CD
,
AD∥
BC
要证:四边形ABCD是平行四边形
解:
是平行四边形。理由如下:
在△ABO和△CDO中,
AO=CO(已知)
∠AOB=∠COD
(对顶角相等)
BO=DO(已知)
∴△ABO≌△CDO
(SAS)
∴
∠ABO=∠ODC
∴AB∥
CD
∴四边形ABCD是平行四边形
同理可证:△ADO≌△CBO
∴
∠DAO=∠BCO
∴AB∥
CD
对角线互相平分的四边形是平行四边形。
几何语言描述判定:
AO=CO
BO=DO
判定定理:
思考:如图,已知四边形ADCB中,
∠A=
∠c,
∠B=
∠D,那么四边形ABCD是平行四边形吗?
几何语言描述判定:
两组对角分别相等的四边形是平行四边形
判定定理:
∠A=
∠c
∠B=
∠D
ABCD
探究3
已知:四边形ABCD中,AB=CD,
AB∥CD
试问:四边
形ABCD是平行四边形吗?请说明理由。
B
解:
连接AC
A
C
D
1
2
是平行四边形,理由如下:
∵
AB∥
CD
∴
∠BAC=∠ACD
在△ABC和△CDA中,
AB=CD
(已知)
∠BAC=∠ACD
(已证)
AC=CA
(公共边)
∴△ABC≌△CDA
(SAS)
∴
∠1=∠2
∴
AD∥
BC
又∵
AB∥
CD
∴四边形ABCD是平行四边形
判定定理:
一组对边平行且相等的四边形是平行四边形。
几何语言描述判定:
ABCD
AD
BC
例:已知平行四边形ABCD中,E.F分别是边AD
BC的中点,求证:EB=DF
证明:∵四边形ABCD是平行四边形
∴AD∥BC
AD=BC
∵
DE=1/2AD
BF=1/2BC
∴DE∥BF
DE=BF
∴四边形EBFD是平行四边形
∴EB=DF
课堂练习:
如图,在四边形ABCD中,
①如果AD=8cm,AB=4cm,且BC=___cm,CD=____cm,那么四边形ABCD是平行四边形。
②∠A=1200,则∠B=____0,∠C=____0,∠D=____0时,四边形ABCD是平行四边形。
③如果AD//BC,AD=6cm,且BC=___cm,那么四边形ABCD是平行四边形。
8
4
点评:两组对边相等的四边形是平行四边形
60
120
60
点评:两组对角相等的四边形是平行四边形
6
点评:一组对边平行且相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
两组邻角分别互补的四边形是平行四边形
对角线互相平分的四边形是平行四边形
∴四边形ABCD是平行四边形
∴AB=CD
AD=BC
∴AB∥CD
AD∥BC
∠ABC=
∠CDA
∠BAD=
∠DCA
∠BAD+∠ABC=180°
∠BCD+∠ABC=180°
归纳小结
一组对边平行且相等的四边形是平行四边形
平行四边形的判定
作业布置
一、第47页练习:
1、2、4题
二、证明两组对角分别相等的四边形是平行四边形。
新课标教学网(www.xkbw.com)--海量教学资源欢迎下载!
再
见
