湘教版八年级下册数学4.3 一次函数的图象课件 (共17张PPT)
文档属性
| 名称 | 湘教版八年级下册数学4.3 一次函数的图象课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 13.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
湘教版八年级数学下册
…
-3
-2
-1
0
1
2
3
…
…
-6
-4
-2
0
2
4
6
…
y
=
2x
y
=
2x
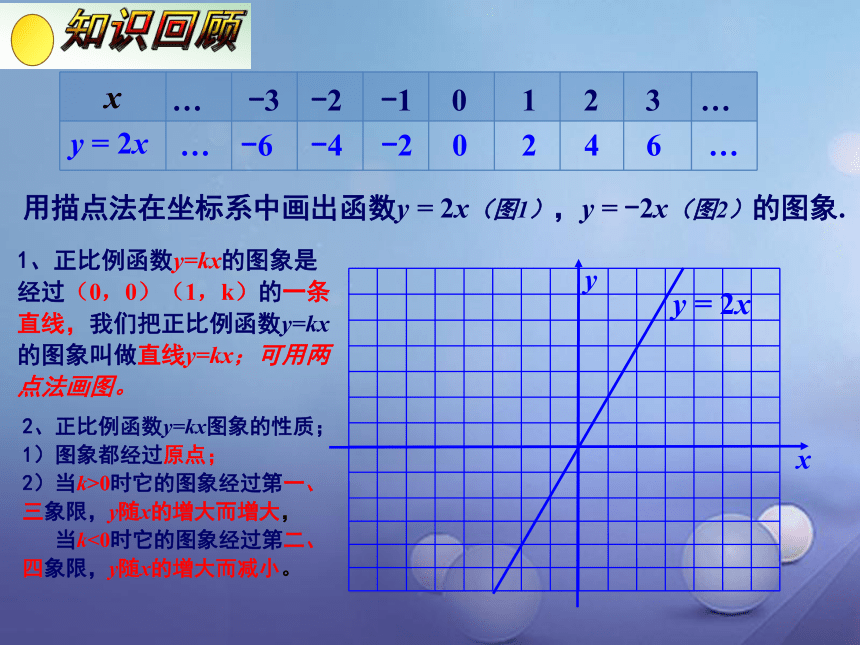
用描点法在坐标系中画出函数y
=
2x(图1),y
=
-2x(图2)的图象.
2、正比例函数y=kx图象的性质;
1)图象都经过原点;
2)当k>0时它的图象经过第一、三象限,y随x的增大而增大,
当k<0时它的图象经过第二、四象限,y随x的增大而减小。
1、正比例函数y=kx的图象是经过(0,0)(1,k)的一条直线,我们把正比例函数y=kx的图象叫做直线y=kx;可用两点法画图。
x
y
=
2x+3
…
-3
-2
-1
0
1
2
3
…
…
-6
-4
-2
0
2
4
6
…
…
-3
-1
1
3
5
7
9
…
y
=
2x
y
=
2x-3
…
-9
-7
-5
-3
-1
1
3
…
y
=
2x
y
=
2x+3
y
=
2x-3
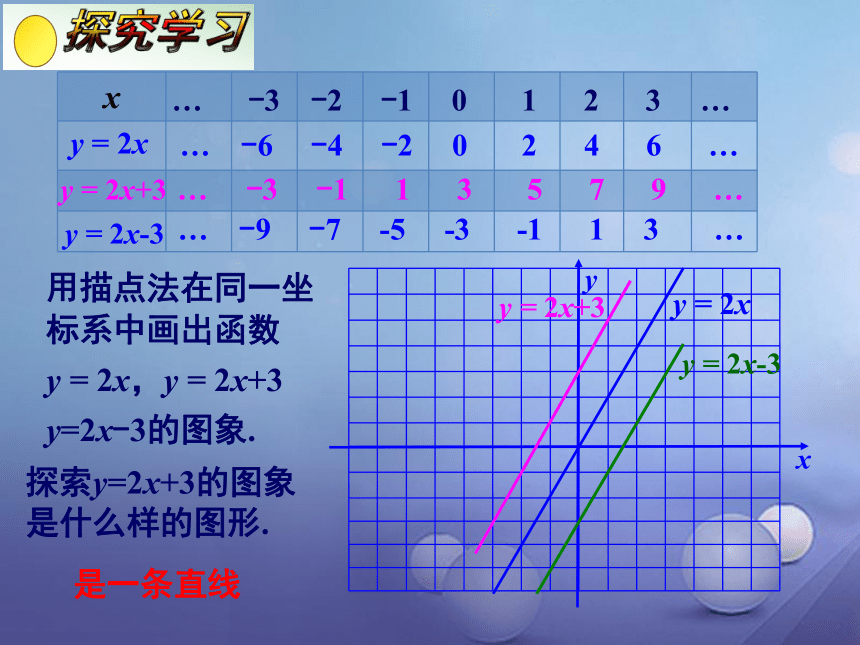
用描点法在同一坐标系中画出函数
y
=
2x,y
=
2x+3
y=2x-3的图象.
探索y=2x+3的图象是什么样的图形.
是一条直线
x
猜测y
=
2x+3的图象与y
=
2x的图象有什么关系?
观察两个函数图象,发现:
都是直线;
倾斜程度相同;
相同点:
不同点:
y=2x的图象过原点;y
=2x+3的图象与y轴交于(0,3)点;
联系:
y=2x+3的图象可以看作是y
=2x的图象向上平移3个长度单位得到;
(平行)
y
=
2x-3的图象与y
=
2x的图象呢?
在图2画出一次函数y
=
-2x+3,y
=
-2x-3的图象.
联系上面问题,考虑一次函数y
=
kx+b的图象是什么形状,它与直线y
=
kx有什么关系?
(1)一次函数y
=
kx+b的图象是
,称它为直线
y=kx+b.图象与y轴的交点为
。
(0,b)
|
b
|
上
下
直线
(2)直线y=kx+b(k≠0)可以看作是
直线y=kx平移
单位而得到。
当b>0时,向
平移,
当b<0时,向
平移。
(必过点)
一次函数
同一平面内,不重合的两直线:
2、b决定与y轴的交点:(0,b)
1、k决定直线的倾斜程度.
一般地,
一次函数y
=
kx+b
(k,b为常数,k≠0)具有如下性质:
k
>
0
k
<
0
函数值
y
随自变量
x
的增大而增大
函数值
y
随自变量
x
的增大而减小
y=kx+b
图
象
函数值y
的变化
讨论:一次函数解析式y=kx+b
(k,
b是常数,k≠0)中,k、b的正负对函数图象有什么影响?
根据图象确定k,b的取值
K
0
b
0
K
0
b
0
K
0
b
0
K
0
b
0
K
0
b
0
K
0
b
0
K
b
>
=
<
=
<
>
<
<
>
<
>
>
分析:小亮骑车离家的距离y是时间x
的函数,这个函数图象由3
条线段组成,每一条线段代表一个阶段的活动.
解:第一段是从原点出发的线段OA.
从横坐标看出,
小亮路上花了30
min,当横坐标从0变化到30
时,纵坐标均匀增加,这说明小亮从家出发匀速前进30
min,到达书店.
例
如图,描述了某一天小亮从家骑车去书店购书,
然后又骑车回家的情况.
你能说出小亮在路上的情形吗?
第二段是与x
轴平行的一条线段AB,当横坐标从30
变化到60时,纵坐标没有变,这说明小亮在书店购书待了30min.
第三段是与x
轴有交点的线段BC.
从横坐标看出,小亮路上花了40min.当横坐标从60
变化到100
时,纵坐标均匀减少,这说明小亮从书店出发匀速前进40min,返回家中.
实际上,我们还可以比较第一段与第三段线段,发现第一段更“陡”,这说明去书店的速度更快,而回家的速度要慢一些.
4.将直线y
=
3x向下平移2个单位,得到直线
;
y
=
3x-2
1.下列函数中,y的值随x值的增大而增大的函数是(
).
A.
y=-2x
B.
y=-2x+1
C.
y=x-2
D.
y=-x-2
C
2.直线y=3x-2可由直线y=3x向
平移
单
位得到.
下
2
3.直线y=x+2可由直线y=x-1向
平移
单位得到。
上
3
5.将直线y=-x-5
向上平移5个单位,得到直
线
.
y
=
-x
6.直线y=-
0.5x+1与x轴的交点为
,
与y轴的交点为
.
(2,0)
(0,1)
7.对于函数y=5x+6,y的值随x的值减小而______.
8.函数y=2x-1经过
象限.
减小
一、三、四
9.
B
10.
11.
C
B
2.一次函数的图象与性质是什么,常数k,b的意义和作用又是什么?.
1.如何画正比例函数、一次函数的图象?
(1)一次函数y
=
kx+b的图象是一条直线(不经过原点),称它为直线y=kx+b.图象与y轴的交点为(0,b)。
(3)当k>0
时,函数值
y
随自变量
x
的增大而增大;当k<0
时,函数值
y
随自变量
x
的增大而减小。
(2)直线y=kx+b(k≠0)可以看作是直线y=kx平移│b│个长度单位而得到。当b>0时,向上平移,当b<0时,向下平移。
作业:p127
A
1
、2
、3
1.一次函数y=kx+b中,kb>0,且y随x的增大而减小,则它的图像大致为(
)。
D
C
B
A
2.直线y=kx+b与直线y=kbx,它们在同一个坐标系中的图像大致为(
)
湘教版八年级数学下册
…
-3
-2
-1
0
1
2
3
…
…
-6
-4
-2
0
2
4
6
…
y
=
2x
y
=
2x
用描点法在坐标系中画出函数y
=
2x(图1),y
=
-2x(图2)的图象.
2、正比例函数y=kx图象的性质;
1)图象都经过原点;
2)当k>0时它的图象经过第一、三象限,y随x的增大而增大,
当k<0时它的图象经过第二、四象限,y随x的增大而减小。
1、正比例函数y=kx的图象是经过(0,0)(1,k)的一条直线,我们把正比例函数y=kx的图象叫做直线y=kx;可用两点法画图。
x
y
=
2x+3
…
-3
-2
-1
0
1
2
3
…
…
-6
-4
-2
0
2
4
6
…
…
-3
-1
1
3
5
7
9
…
y
=
2x
y
=
2x-3
…
-9
-7
-5
-3
-1
1
3
…
y
=
2x
y
=
2x+3
y
=
2x-3
用描点法在同一坐标系中画出函数
y
=
2x,y
=
2x+3
y=2x-3的图象.
探索y=2x+3的图象是什么样的图形.
是一条直线
x
猜测y
=
2x+3的图象与y
=
2x的图象有什么关系?
观察两个函数图象,发现:
都是直线;
倾斜程度相同;
相同点:
不同点:
y=2x的图象过原点;y
=2x+3的图象与y轴交于(0,3)点;
联系:
y=2x+3的图象可以看作是y
=2x的图象向上平移3个长度单位得到;
(平行)
y
=
2x-3的图象与y
=
2x的图象呢?
在图2画出一次函数y
=
-2x+3,y
=
-2x-3的图象.
联系上面问题,考虑一次函数y
=
kx+b的图象是什么形状,它与直线y
=
kx有什么关系?
(1)一次函数y
=
kx+b的图象是
,称它为直线
y=kx+b.图象与y轴的交点为
。
(0,b)
|
b
|
上
下
直线
(2)直线y=kx+b(k≠0)可以看作是
直线y=kx平移
单位而得到。
当b>0时,向
平移,
当b<0时,向
平移。
(必过点)
一次函数
同一平面内,不重合的两直线:
2、b决定与y轴的交点:(0,b)
1、k决定直线的倾斜程度.
一般地,
一次函数y
=
kx+b
(k,b为常数,k≠0)具有如下性质:
k
>
0
k
<
0
函数值
y
随自变量
x
的增大而增大
函数值
y
随自变量
x
的增大而减小
y=kx+b
图
象
函数值y
的变化
讨论:一次函数解析式y=kx+b
(k,
b是常数,k≠0)中,k、b的正负对函数图象有什么影响?
根据图象确定k,b的取值
K
0
b
0
K
0
b
0
K
0
b
0
K
0
b
0
K
0
b
0
K
0
b
0
K
b
>
=
<
=
<
>
<
<
>
<
>
>
分析:小亮骑车离家的距离y是时间x
的函数,这个函数图象由3
条线段组成,每一条线段代表一个阶段的活动.
解:第一段是从原点出发的线段OA.
从横坐标看出,
小亮路上花了30
min,当横坐标从0变化到30
时,纵坐标均匀增加,这说明小亮从家出发匀速前进30
min,到达书店.
例
如图,描述了某一天小亮从家骑车去书店购书,
然后又骑车回家的情况.
你能说出小亮在路上的情形吗?
第二段是与x
轴平行的一条线段AB,当横坐标从30
变化到60时,纵坐标没有变,这说明小亮在书店购书待了30min.
第三段是与x
轴有交点的线段BC.
从横坐标看出,小亮路上花了40min.当横坐标从60
变化到100
时,纵坐标均匀减少,这说明小亮从书店出发匀速前进40min,返回家中.
实际上,我们还可以比较第一段与第三段线段,发现第一段更“陡”,这说明去书店的速度更快,而回家的速度要慢一些.
4.将直线y
=
3x向下平移2个单位,得到直线
;
y
=
3x-2
1.下列函数中,y的值随x值的增大而增大的函数是(
).
A.
y=-2x
B.
y=-2x+1
C.
y=x-2
D.
y=-x-2
C
2.直线y=3x-2可由直线y=3x向
平移
单
位得到.
下
2
3.直线y=x+2可由直线y=x-1向
平移
单位得到。
上
3
5.将直线y=-x-5
向上平移5个单位,得到直
线
.
y
=
-x
6.直线y=-
0.5x+1与x轴的交点为
,
与y轴的交点为
.
(2,0)
(0,1)
7.对于函数y=5x+6,y的值随x的值减小而______.
8.函数y=2x-1经过
象限.
减小
一、三、四
9.
B
10.
11.
C
B
2.一次函数的图象与性质是什么,常数k,b的意义和作用又是什么?.
1.如何画正比例函数、一次函数的图象?
(1)一次函数y
=
kx+b的图象是一条直线(不经过原点),称它为直线y=kx+b.图象与y轴的交点为(0,b)。
(3)当k>0
时,函数值
y
随自变量
x
的增大而增大;当k<0
时,函数值
y
随自变量
x
的增大而减小。
(2)直线y=kx+b(k≠0)可以看作是直线y=kx平移│b│个长度单位而得到。当b>0时,向上平移,当b<0时,向下平移。
作业:p127
A
1
、2
、3
1.一次函数y=kx+b中,kb>0,且y随x的增大而减小,则它的图像大致为(
)。
D
C
B
A
2.直线y=kx+b与直线y=kbx,它们在同一个坐标系中的图像大致为(
)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
