华东师大版八年级下册数学18.2平行四边形的判定的应用课件(第3课时 共16张PPT)
文档属性
| 名称 | 华东师大版八年级下册数学18.2平行四边形的判定的应用课件(第3课时 共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 282.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 15:06:14 | ||
图片预览






文档简介
(共16张PPT)
课前准备:
结合课本,复习平行四边形的性质与判断定理
(1)我们已经学习的平行四边形的性质有哪些?
①边
②角
③对角线
(2)我们已经学习的平行四边形的判定方法有哪些?
①定义
②边
③对角线
18.2.3平行四边形的判定的应用
教学目标:
1.掌握平行四边形的判定定理
2.综合运用平行四边形判定定理解决问题
重点:
平行四边形的判定定理
难点:
平行四边形判定定理的综合运用
探究点一:知识回顾
要点回顾:
我们已经学习的平行四边形的判定方法有哪些?
①定义
②边
③对角线
平行四边形的判定方法
(1)定义
两组对边分别平行的四边形是平行四边形
(2)判定定理
①两组对边分别相等的四边形是平行四边形(边)
②一组对边平行且相等的四边形是平行四边形(边)③对角线互相平分的四边形是平行四边形(对角线)
探究点二:平行四边形判定应用
自学指导一:
内容:课本88页
时间:5分钟
完成:认真看课本例3、例4,规范证明步骤和书写格式
探究点二:综合应用
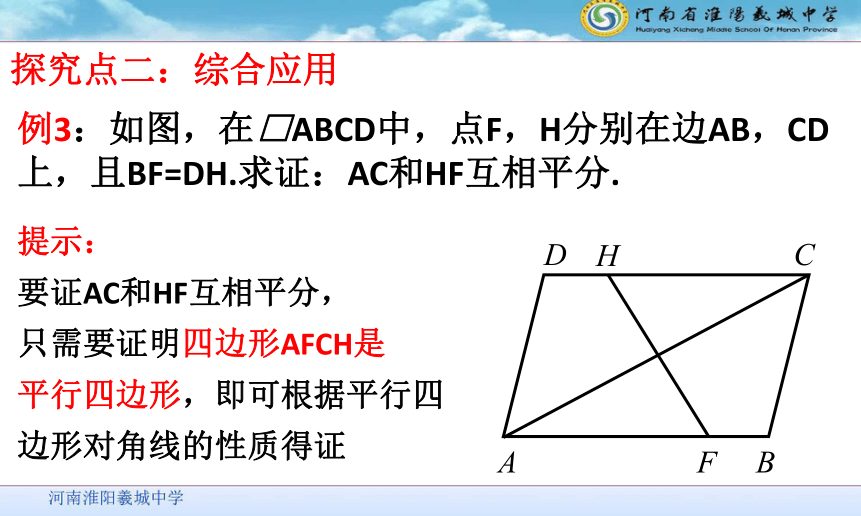
例3:如图,在□ABCD中,点F,H分别在边AB,CD上,且BF=DH.求证:AC和HF互相平分.
提示:
要证AC和HF互相平分,
只需要证明四边形AFCH是
平行四边形,即可根据平行四边形对角线的性质得证
证明:连结AH、CF
∵四边形ABCD是平行四边形
∴AB//CD,AB=CD
又∵BF=DH
∴AB-BF=CD-DH
即AF=CH
∴四边形AFCH是平行四边形
∴AC和HF互相平分
例4:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形
提示:
根据已经学习的判定方法,由已知的条件可以通过哪种方法判定四边形ABCD是平行四边形
证明:
在四边形ABCD中,
∵∠A+∠B+∠C+∠D=360°
且∠A=∠C,∠B=∠D
∴∠A+∠B+∠A+∠B=360°
即2(∠A+∠B)=360°
∴∠A+∠B=180°
∴AD//CB.同理可证:AB//CD
∴四边形ABCD是平行四边形
通过这个题目,你有什么发现?
巩固训练:
1、如图,在□ABCD中,AF=CH,DE=BG
求证:EG和HF互相平分
巩固训练:
如图,在□ABCD中,
AF=CH,DE=BG
求证:EG和HF互相
平分
证明:∵AB=CD,AF=CH
∴AB-AF=CD-CH,即BF=DH
又∵∠B=∠D,BG=DE
∴△FBG≌△HDE(S.A.S.)
∴FG=HE,同理可证EF=GH
∴四边形EFGH是平行四边形
∴EG和HF互相平分
针对训练:
2、在四边形ABCD中,AB//CD,∠B=∠D
求证:四边形ABCD是平行四边形
针对训练:
在四边形ABCD中,AB//CD,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∵AB//CD,
∴∠B+∠C=180°
又∵∠B=∠D
∴∠D+∠C=180°(等量代换)
∴AD//BC
∴四边形ABCD是平行四边形
通过这个题目,你有什么发现?
课堂小结
平行四边形的判定方法有哪些?
①定义
②边
③对角线
检测指导:
1、
闭卷检测,独立完成(6分钟)
2、
对子互批,自主纠错(1分钟)
3、
小组汇报,师生点拨(1分钟)
达标检测,当堂反馈(8分钟)
课前准备:
结合课本,复习平行四边形的性质与判断定理
(1)我们已经学习的平行四边形的性质有哪些?
①边
②角
③对角线
(2)我们已经学习的平行四边形的判定方法有哪些?
①定义
②边
③对角线
18.2.3平行四边形的判定的应用
教学目标:
1.掌握平行四边形的判定定理
2.综合运用平行四边形判定定理解决问题
重点:
平行四边形的判定定理
难点:
平行四边形判定定理的综合运用
探究点一:知识回顾
要点回顾:
我们已经学习的平行四边形的判定方法有哪些?
①定义
②边
③对角线
平行四边形的判定方法
(1)定义
两组对边分别平行的四边形是平行四边形
(2)判定定理
①两组对边分别相等的四边形是平行四边形(边)
②一组对边平行且相等的四边形是平行四边形(边)③对角线互相平分的四边形是平行四边形(对角线)
探究点二:平行四边形判定应用
自学指导一:
内容:课本88页
时间:5分钟
完成:认真看课本例3、例4,规范证明步骤和书写格式
探究点二:综合应用
例3:如图,在□ABCD中,点F,H分别在边AB,CD上,且BF=DH.求证:AC和HF互相平分.
提示:
要证AC和HF互相平分,
只需要证明四边形AFCH是
平行四边形,即可根据平行四边形对角线的性质得证
证明:连结AH、CF
∵四边形ABCD是平行四边形
∴AB//CD,AB=CD
又∵BF=DH
∴AB-BF=CD-DH
即AF=CH
∴四边形AFCH是平行四边形
∴AC和HF互相平分
例4:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形
提示:
根据已经学习的判定方法,由已知的条件可以通过哪种方法判定四边形ABCD是平行四边形
证明:
在四边形ABCD中,
∵∠A+∠B+∠C+∠D=360°
且∠A=∠C,∠B=∠D
∴∠A+∠B+∠A+∠B=360°
即2(∠A+∠B)=360°
∴∠A+∠B=180°
∴AD//CB.同理可证:AB//CD
∴四边形ABCD是平行四边形
通过这个题目,你有什么发现?
巩固训练:
1、如图,在□ABCD中,AF=CH,DE=BG
求证:EG和HF互相平分
巩固训练:
如图,在□ABCD中,
AF=CH,DE=BG
求证:EG和HF互相
平分
证明:∵AB=CD,AF=CH
∴AB-AF=CD-CH,即BF=DH
又∵∠B=∠D,BG=DE
∴△FBG≌△HDE(S.A.S.)
∴FG=HE,同理可证EF=GH
∴四边形EFGH是平行四边形
∴EG和HF互相平分
针对训练:
2、在四边形ABCD中,AB//CD,∠B=∠D
求证:四边形ABCD是平行四边形
针对训练:
在四边形ABCD中,AB//CD,∠B=∠D
求证:四边形ABCD是平行四边形
证明:∵AB//CD,
∴∠B+∠C=180°
又∵∠B=∠D
∴∠D+∠C=180°(等量代换)
∴AD//BC
∴四边形ABCD是平行四边形
通过这个题目,你有什么发现?
课堂小结
平行四边形的判定方法有哪些?
①定义
②边
③对角线
检测指导:
1、
闭卷检测,独立完成(6分钟)
2、
对子互批,自主纠错(1分钟)
3、
小组汇报,师生点拨(1分钟)
达标检测,当堂反馈(8分钟)
