六年级下册数学课件 -《信息窗一(比例的意义)》 青岛版 (共19张PPT)
文档属性
| 名称 | 六年级下册数学课件 -《信息窗一(比例的意义)》 青岛版 (共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
比例的意义
青岛版六年级下册
麦芽过程
啤酒生产流程
糖化过程
发酵过程
灌装过程
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
一辆货车两天运输麦芽情况
第一天 第二天
运输量(吨) 16 32
运输次数 2 4
两天运输量与运输次数的
的比值分别是多少?
第一天运输量与运输次数的比值:
第二天运输量与运输次数的比值:
16 :2 =
32 :4 =
8
8
求出它们的比值,你发现了什么?
16︰2
32︰4
=
=
或
表示两个比相等的式子叫做比例。
(分数形式)
我发现运输量和运输次数的比值是相等的。
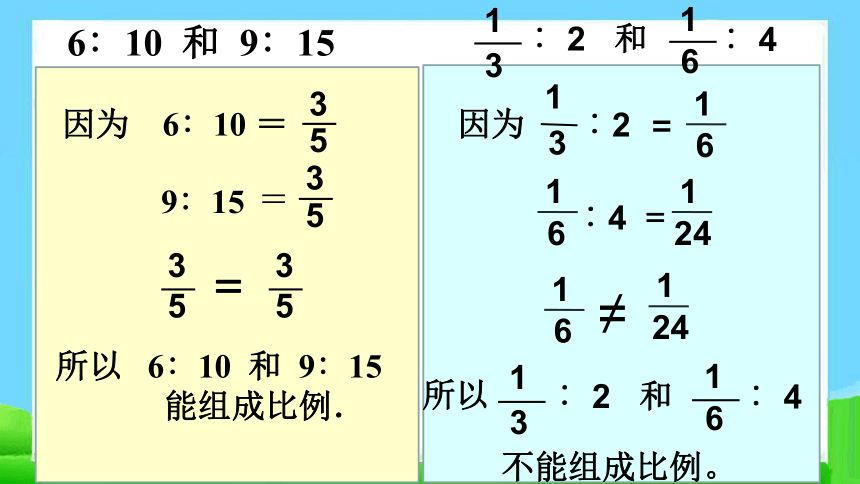
6∶10 和 9∶15
3
1
︰
2
1
6
︰
4
和
判断两个比能不能组成比例,可以根据比例的意义,看它们的比值是否相等。
6∶10 和 9∶15
所以 6∶10 和 9∶15
能组成比例.
因为 6∶10 =
3
5
9∶15 =
3
5
=
3
5
3
5
3
1
︰
2
1
6
︰
4
和
3
1
︰2 =
因为
1
6
︰4 =
1
6
1
24
1
6
≠
1
24
所以
不能组成比例。
3
1
︰
2
1
6
︰
4
和
二、合作探索
在探索比例意义的活动中,我们经历了怎样一个学习过程?
观察数据
分析数据
总结概念
16 :2 = 32 :4
运输量和运输次数的比值是相等的。
表示两个比相等的式子叫做比例。
看书37页,指出下面比例的外项和内项。
16 ∶ 2 = 32 ∶ 4
∶
=
6 ∶ 4
外项
外项
内项
内项
16
2
=
32
4
比和比例有什么区别和联系?
1
比由2个数组成,表示两个数相除。
比和比例的区别和联系
2
比例由4个数组成,表示两个比的比值相等,是一个等式。
3
比是比例的一部分,比例由两个比值相等的比组成。
基础练习
综合练习
开放练习
作业设计
基础练习
填空:
1、用18的四个因数组成一组比例是( )
2、写出比值是0.4的两个比,并组成比例( )
1:2=3:6
2:5=4:10
基础练习
应用比例的意义,判断下面两个比能不能组成比例。
6∶9 和 9∶12
1.4∶2 和 28∶40
不能组成比例
能组成比例
选择题
(1)( )是比例。
A. 10:6 B. 5 : 3=0.6 C. 20:4=5:1
(2) 4 : 5 与( ) 能组成比例。
A. 5 : 4 B. 8:10 C. 15 : 12
C
B
基础练习
把能组成比例的比连起来
综合练习
开放练习
15,6,30,3这四个数可以组成比例吗?如果可以,请你写出来。
名侦探柯南:
在一个案发现场,测量出嫌疑人的脚长大约是26厘米,柯南很快就知道嫌疑人身高大约是多少。他是怎么知道的呢?
科学研究发现,人的身高和脚长的比大约是7:1。
也就是身高是脚长的7倍,所以身高为26×7=182(厘米)。你能根据这些信息写出比例吗?
比例的意义
青岛版六年级下册
麦芽过程
啤酒生产流程
糖化过程
发酵过程
灌装过程
从图中,你知道了哪些数学信息?
根据这些信息,你能提出什么问题?
一辆货车两天运输麦芽情况
第一天 第二天
运输量(吨) 16 32
运输次数 2 4
两天运输量与运输次数的
的比值分别是多少?
第一天运输量与运输次数的比值:
第二天运输量与运输次数的比值:
16 :2 =
32 :4 =
8
8
求出它们的比值,你发现了什么?
16︰2
32︰4
=
=
或
表示两个比相等的式子叫做比例。
(分数形式)
我发现运输量和运输次数的比值是相等的。
6∶10 和 9∶15
3
1
︰
2
1
6
︰
4
和
判断两个比能不能组成比例,可以根据比例的意义,看它们的比值是否相等。
6∶10 和 9∶15
所以 6∶10 和 9∶15
能组成比例.
因为 6∶10 =
3
5
9∶15 =
3
5
=
3
5
3
5
3
1
︰
2
1
6
︰
4
和
3
1
︰2 =
因为
1
6
︰4 =
1
6
1
24
1
6
≠
1
24
所以
不能组成比例。
3
1
︰
2
1
6
︰
4
和
二、合作探索
在探索比例意义的活动中,我们经历了怎样一个学习过程?
观察数据
分析数据
总结概念
16 :2 = 32 :4
运输量和运输次数的比值是相等的。
表示两个比相等的式子叫做比例。
看书37页,指出下面比例的外项和内项。
16 ∶ 2 = 32 ∶ 4
∶
=
6 ∶ 4
外项
外项
内项
内项
16
2
=
32
4
比和比例有什么区别和联系?
1
比由2个数组成,表示两个数相除。
比和比例的区别和联系
2
比例由4个数组成,表示两个比的比值相等,是一个等式。
3
比是比例的一部分,比例由两个比值相等的比组成。
基础练习
综合练习
开放练习
作业设计
基础练习
填空:
1、用18的四个因数组成一组比例是( )
2、写出比值是0.4的两个比,并组成比例( )
1:2=3:6
2:5=4:10
基础练习
应用比例的意义,判断下面两个比能不能组成比例。
6∶9 和 9∶12
1.4∶2 和 28∶40
不能组成比例
能组成比例
选择题
(1)( )是比例。
A. 10:6 B. 5 : 3=0.6 C. 20:4=5:1
(2) 4 : 5 与( ) 能组成比例。
A. 5 : 4 B. 8:10 C. 15 : 12
C
B
基础练习
把能组成比例的比连起来
综合练习
开放练习
15,6,30,3这四个数可以组成比例吗?如果可以,请你写出来。
名侦探柯南:
在一个案发现场,测量出嫌疑人的脚长大约是26厘米,柯南很快就知道嫌疑人身高大约是多少。他是怎么知道的呢?
科学研究发现,人的身高和脚长的比大约是7:1。
也就是身高是脚长的7倍,所以身高为26×7=182(厘米)。你能根据这些信息写出比例吗?
