人教版八年级数学下册 20.1.2 中位数和众数课件( 第2课时 共17张PPT)
文档属性
| 名称 | 人教版八年级数学下册 20.1.2 中位数和众数课件( 第2课时 共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 382.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第二十章
数据的分析
20.1.2
中位数和众数
第2课时
20.1
数据的集中趋势
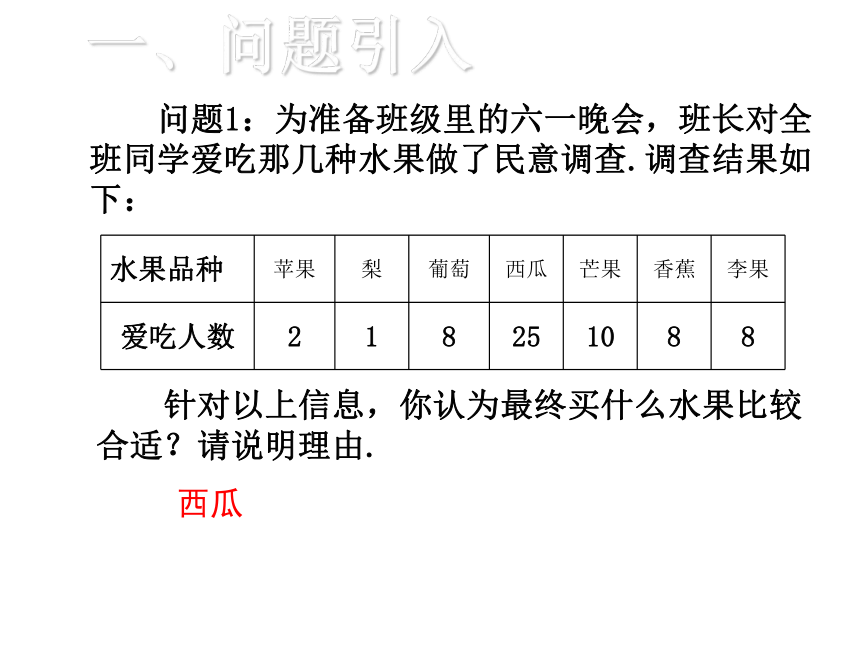
问题1:为准备班级里的六一晚会,班长对全班同学爱吃那几种水果做了民意调查.调查结果如下:
一、问题引入
针对以上信息,你认为最终买什么水果比较合适?请说明理由.
西瓜
水果品种
苹果
梨
葡萄
西瓜
芒果
香蕉
李果
爱吃人数
2
1
8
25
10
8
8
二、探究新知
请举一些生活中运用众数的例子.
求下列各组数据的众数:
zx``x```k
(1)2,5,3,5,1,5,4;
(2)5,2,6,7,6,3,3,4,3,7,6;
(3)2,2,3,3,4;
(4)2,2,3,3,4,4;
(5)1,2,3,5,7.
一组数据可以有不止一个众数,也可以没有众数.
一组数据中出现次数最多的数据是这组数据的众数.
5
3
6,
3
2,
3,
2,
4
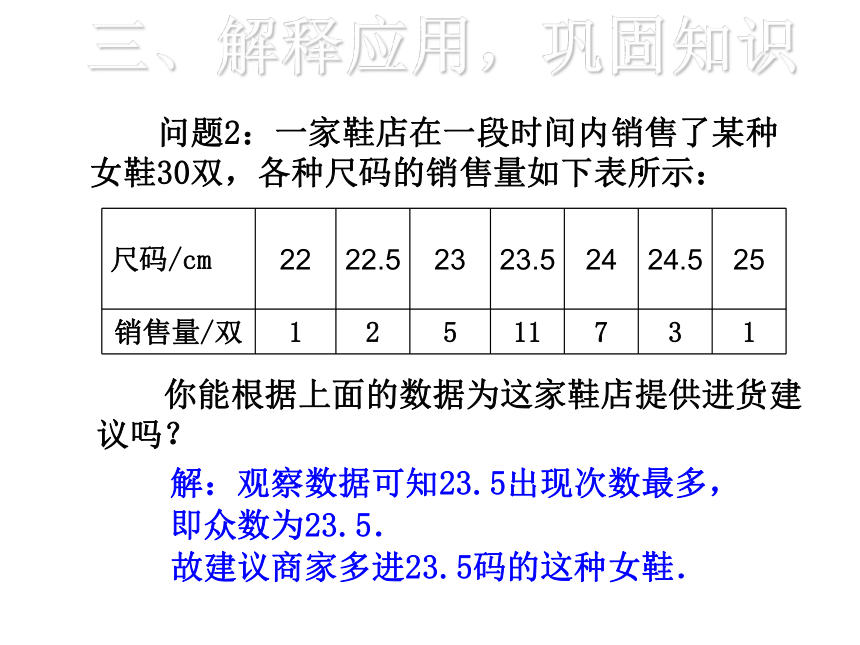
问题2:一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表所示:
你能根据上面的数据为这家鞋店提供进货建议吗?
三、解释应用,巩固知识
解:观察数据可知23.5出现次数最多,
即众数为23.5.
故建议商家多进23.5码的这种女鞋.
尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
问题3:老师想知道学生每天在上学路上所花的时间,于是让大家把每天来校上课的单程时间写在纸上,下面是全班30名学生单程所花的时间(分):
(1)求学生上学单程所花时间的平均数、中位数、众数.
(2)假如老师随机地问一个学生,你认为老师最可能得到的回答是多少分钟?
20
30
15
20
25
5
15
20
10
35
45
10
20
25
30
20
15
20
20
10
20
5
15
20
20
5
15
20
巩固练习:教材第118页练习第1、2题.
四、小结
1.中数的定义和现实意义.
2.众数的特点及其与平均数、中位数的区别与联系.
用众数作一组数据的代表数,其优点是计算最小,不受极端数值的影响;缺点是可靠性小,局限性大,只有在一组数据中不少数据重复出现时,才适合用众数表示.
3.反思拓展:
八年级有十个班级,如果已知在一次测试中这十个班的平均分,也知道各班级的人数,那么我们可以计算出整个年级的平均分;如果已知的是每个班级的中位数或者是众数,那么我们能得到整个年级的中位数或者众数吗?
Z```x``xk
五、作业设计
1.必做题:
(1)在某电视台举办的歌咏比赛中,六位评委给1号选手的评分如下:90,96,91,96,95,94,这组数据的众数是(
)
A.94.5
B.95
C.96
D.2
(2)八年级一班46名同学中,13岁的有5人,14岁的有20人,15岁的有15人,16岁的有6人,八年级一班学生年龄的平均数、中位数、众数分别是多少?
P119例题6:某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成情况对营业员进行适当的奖惩.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元)
,数据如下:
18
16
13
24
15
28
26
18
19
17
16
19
32
30
16
14
15
26
15
32
23
17
15
15
28
28
16
19
三、问题的变化与深入
(1)月销售额在哪个值的人数最多?中间的销售额是多少?平均的月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
解:(1)分析数据:样本中,15出现的次数最多;故样本众数为15,所以月销售额在15万元人数最多;
将数据从小到大排列,找最中间的两个数都为18,故中位数是18,所以中间的月销售额是18万元;
根据平均数的求法,平均数为(17+18+16+13+24+15+…+28+28+16+19)÷30≈20.
故这组数据的平均数约是20,所以平均的月销售额是20万元.
(2)如果想确定一个较高的目标,这个目标可以定为20万元(平均数),因为从平均数、中位数、众数中,平均数最大.可以估计月销售额定为每月20万元是一个较高的目标,大约会有
的营业员获得奖励.
(3)如果想让一半左右的营业员都能达到目标,月销售额可以定为18万元(中位数),因为从样本情况看,月销售额在18万元以上(含18万元)的有15人,占总人数的一半左右,可以估计,每月销售额定为18万元,可以估计一半左右的营业员获得奖励.
(3)下图反映了八年级(9)班40名学生在一次数学测验中的成绩.
①从图中观察这个班这次数学测验成绩的中位数和众数;
②根据图形估计这个班这次数学测验成绩的平均成绩.
zx``x````k
分数
人数
2.选做题:
(1)某市举行一次少年滑冰比赛,各年龄组的参赛人数如下表所示:
①求全体参赛选手年龄的众数、中位数.
②小明说,他所在年龄组的参赛人数占全体参赛人数的28%,你认为小明是哪个年龄组的选手?请说明理由.
年龄组
13岁
14岁
15岁
16岁
参赛人数
5
19
12
14
(2)某公司销售人员有15人,销售部为了制定某种商品的月销售额,统计了这15人某月的销售量如下所示:
①求该月销售量的平均数、中位数和众数.
②假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?请你制定一个较合理的销售定额,并说明理由.
每人销售量/件
1800
510
250
210
150
120
人数
1
1
3
5
3
2
3.备选题:
(1)某移动公司为了调查手机发送短信的情况,在本区域的1
000位用户中抽取了10位用户来统计他们某月发送短信息的条数,结果如下表所示:
则本次调查中抽取的样本容量是
,中位数是
,众数是
.
手机用户序号
1
2
3
4
5
6
7
8
9
10
发送短信息条数
85
78
83
79
84
85
86
88
80
85
谢谢大家!
第二十章
数据的分析
20.1.2
中位数和众数
第2课时
20.1
数据的集中趋势
问题1:为准备班级里的六一晚会,班长对全班同学爱吃那几种水果做了民意调查.调查结果如下:
一、问题引入
针对以上信息,你认为最终买什么水果比较合适?请说明理由.
西瓜
水果品种
苹果
梨
葡萄
西瓜
芒果
香蕉
李果
爱吃人数
2
1
8
25
10
8
8
二、探究新知
请举一些生活中运用众数的例子.
求下列各组数据的众数:
zx``x```k
(1)2,5,3,5,1,5,4;
(2)5,2,6,7,6,3,3,4,3,7,6;
(3)2,2,3,3,4;
(4)2,2,3,3,4,4;
(5)1,2,3,5,7.
一组数据可以有不止一个众数,也可以没有众数.
一组数据中出现次数最多的数据是这组数据的众数.
5
3
6,
3
2,
3,
2,
4
问题2:一家鞋店在一段时间内销售了某种女鞋30双,各种尺码的销售量如下表所示:
你能根据上面的数据为这家鞋店提供进货建议吗?
三、解释应用,巩固知识
解:观察数据可知23.5出现次数最多,
即众数为23.5.
故建议商家多进23.5码的这种女鞋.
尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
问题3:老师想知道学生每天在上学路上所花的时间,于是让大家把每天来校上课的单程时间写在纸上,下面是全班30名学生单程所花的时间(分):
(1)求学生上学单程所花时间的平均数、中位数、众数.
(2)假如老师随机地问一个学生,你认为老师最可能得到的回答是多少分钟?
20
30
15
20
25
5
15
20
10
35
45
10
20
25
30
20
15
20
20
10
20
5
15
20
20
5
15
20
巩固练习:教材第118页练习第1、2题.
四、小结
1.中数的定义和现实意义.
2.众数的特点及其与平均数、中位数的区别与联系.
用众数作一组数据的代表数,其优点是计算最小,不受极端数值的影响;缺点是可靠性小,局限性大,只有在一组数据中不少数据重复出现时,才适合用众数表示.
3.反思拓展:
八年级有十个班级,如果已知在一次测试中这十个班的平均分,也知道各班级的人数,那么我们可以计算出整个年级的平均分;如果已知的是每个班级的中位数或者是众数,那么我们能得到整个年级的中位数或者众数吗?
Z```x``xk
五、作业设计
1.必做题:
(1)在某电视台举办的歌咏比赛中,六位评委给1号选手的评分如下:90,96,91,96,95,94,这组数据的众数是(
)
A.94.5
B.95
C.96
D.2
(2)八年级一班46名同学中,13岁的有5人,14岁的有20人,15岁的有15人,16岁的有6人,八年级一班学生年龄的平均数、中位数、众数分别是多少?
P119例题6:某商场服装部为了调动营业员的积极性,决定实行目标管理,根据目标完成情况对营业员进行适当的奖惩.为了确定一个适当的月销售目标,商场服装部统计了每个营业员在某月的销售额(单位:万元)
,数据如下:
18
16
13
24
15
28
26
18
19
17
16
19
32
30
16
14
15
26
15
32
23
17
15
15
28
28
16
19
三、问题的变化与深入
(1)月销售额在哪个值的人数最多?中间的销售额是多少?平均的月销售额是多少?
(2)如果想确定一个较高的销售目标,你认为月销售额定为多少合适?说明理由.
(3)如果想让一半左右的营业员都能达到销售目标,你认为月销售额定为多少合适?说明理由.
解:(1)分析数据:样本中,15出现的次数最多;故样本众数为15,所以月销售额在15万元人数最多;
将数据从小到大排列,找最中间的两个数都为18,故中位数是18,所以中间的月销售额是18万元;
根据平均数的求法,平均数为(17+18+16+13+24+15+…+28+28+16+19)÷30≈20.
故这组数据的平均数约是20,所以平均的月销售额是20万元.
(2)如果想确定一个较高的目标,这个目标可以定为20万元(平均数),因为从平均数、中位数、众数中,平均数最大.可以估计月销售额定为每月20万元是一个较高的目标,大约会有
的营业员获得奖励.
(3)如果想让一半左右的营业员都能达到目标,月销售额可以定为18万元(中位数),因为从样本情况看,月销售额在18万元以上(含18万元)的有15人,占总人数的一半左右,可以估计,每月销售额定为18万元,可以估计一半左右的营业员获得奖励.
(3)下图反映了八年级(9)班40名学生在一次数学测验中的成绩.
①从图中观察这个班这次数学测验成绩的中位数和众数;
②根据图形估计这个班这次数学测验成绩的平均成绩.
zx``x````k
分数
人数
2.选做题:
(1)某市举行一次少年滑冰比赛,各年龄组的参赛人数如下表所示:
①求全体参赛选手年龄的众数、中位数.
②小明说,他所在年龄组的参赛人数占全体参赛人数的28%,你认为小明是哪个年龄组的选手?请说明理由.
年龄组
13岁
14岁
15岁
16岁
参赛人数
5
19
12
14
(2)某公司销售人员有15人,销售部为了制定某种商品的月销售额,统计了这15人某月的销售量如下所示:
①求该月销售量的平均数、中位数和众数.
②假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?请你制定一个较合理的销售定额,并说明理由.
每人销售量/件
1800
510
250
210
150
120
人数
1
1
3
5
3
2
3.备选题:
(1)某移动公司为了调查手机发送短信的情况,在本区域的1
000位用户中抽取了10位用户来统计他们某月发送短信息的条数,结果如下表所示:
则本次调查中抽取的样本容量是
,中位数是
,众数是
.
手机用户序号
1
2
3
4
5
6
7
8
9
10
发送短信息条数
85
78
83
79
84
85
86
88
80
85
谢谢大家!
