沪科版九年级下册数学 24.3 圆周角定理及其推论 课件(共19张PPT)
文档属性
| 名称 | 沪科版九年级下册数学 24.3 圆周角定理及其推论 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 615.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
24.3圆周角
一、引入
问题1:如图,在足球比赛场上,甲、乙,丙三名队员分别站在A、B,C三处,都能向对方球门MN进攻.且水平相当,此时,队友丁将球传给谁射门更好呢?为什么?传给乙和丙呢?(不考虑其他因素)
问题2:
(1)、圆心角的定义?
(2)、圆心角的度数与它所对的弧之间有什么关系?
一、引入
二、读
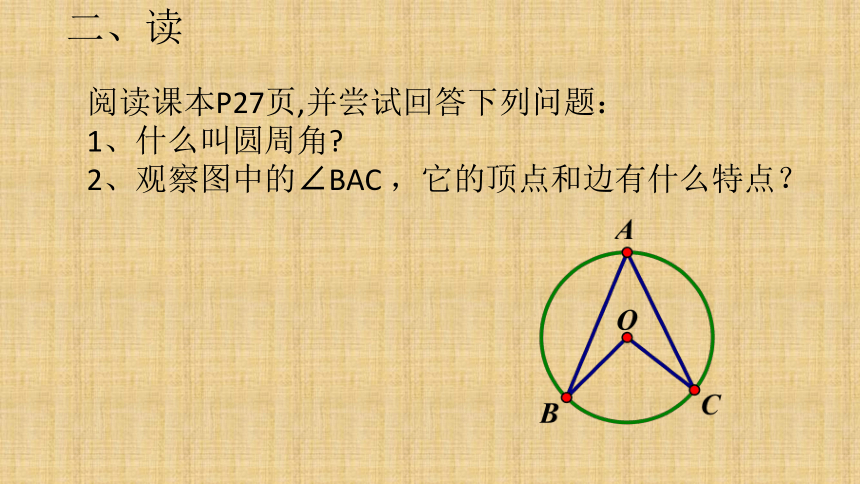
阅读课本P27页,并尝试回答下列问题:
1、什么叫圆周角?
2、观察图中的∠BAC
,它的顶点和边有什么特点?
圆周角:顶点在圆上,两边都与圆相交的角叫
圆周角.
归纳定义:
注意:(1)顶点在圆上,
(2)角的两边分别和圆相交.
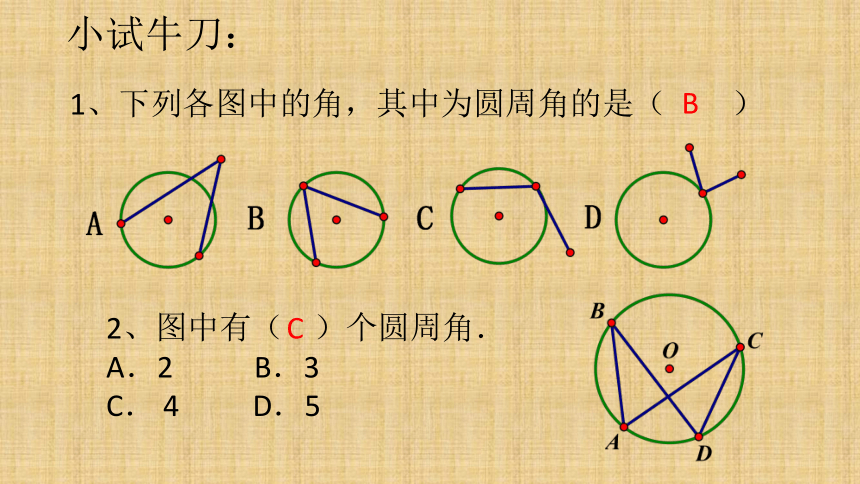
小试牛刀:
1、下列各图中的角,其中为圆周角的是( )
2、图中有(
)个圆周角.
A.2
B.3
C.
4
D.5
B
C
三、探
观察下列操作,请你回答下列问题:
1、圆心和圆周角有几种位置关系?
环节一
(1)圆周角和圆心的位置关系的种类:
三、探
(2)猜想在上述三种情形下,在⊙O中,弧BC所对圆周角∠BAC和圆心角∠BOC有怎样的数量关系?并进行说理。
D
D
图1
图2
图3
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
(3)
圆心O在∠BAC的外部
环节二
1、通过以上的猜想论证你能用一句话来概括你的发现吗?先说给你的同桌听听。
三、探
2、你能用几何语言来描述这个定理吗?
?
一条弧所对的圆周角等于它所对圆心角的一半。
四、练:
3、已知三角形ABC为等边三角形,点O为圆心,,圆周角∠A=
,圆心角∠BOC=
60?
120?
4、已知:如图,在圆O中,∠BOC=50°,求∠W的大小
四、练
审题要仔细呦!
变式2
已知:在⊙O中,∠BOC=50°
如果BC=CE,求∠D的大小
变式1
在⊙O中,BC50°
,W是圆O上异于B、C的一点,求∠W的大小
user:
user:
由变式1、2的练习,你能得出什么结论?请说给你小组内的同学听,告诉他们,你的发现.
思考:
W’
在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
圆周角定理推论1
总结归纳:
5、如图,AC是圆O的直径,
则∠ADC
=
,
∠ABC=
.
90°
90°
推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
四、练
6.
如图,在△ABC中,AB=AC,以AB为直径的圆交BC于D,交AC于E.
(1)
BD与CD的大小有什么关系?为什么?
A
B
C
D
E
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
又∵AB=AC,
∴△ABC为等腰三角形,∴BD=CD.
解:(1)BD=CD.
理由如下:连接AD,
(2)
求证:
.
(2)证明∵
△ABC为等腰三角形,AD⊥BC,
∴∠BAD=∠CAD.
∴
问题1:如图,在足球比赛场上,甲、乙,丙三名队员分别站在A、B,C三处,都能向对方球门MN进攻.且水平相当,此时,队友丁将球传给谁射门更好呢?为什么?传给乙和丙呢?(不考虑其他因素)
问题解决:
谈谈本节课你的收获和不足?
(知识,方法,体会)
五
结:
作业布置:
作业:课本P29
练习
T3
P31
习题24.3
T4
24.3圆周角
一、引入
问题1:如图,在足球比赛场上,甲、乙,丙三名队员分别站在A、B,C三处,都能向对方球门MN进攻.且水平相当,此时,队友丁将球传给谁射门更好呢?为什么?传给乙和丙呢?(不考虑其他因素)
问题2:
(1)、圆心角的定义?
(2)、圆心角的度数与它所对的弧之间有什么关系?
一、引入
二、读
阅读课本P27页,并尝试回答下列问题:
1、什么叫圆周角?
2、观察图中的∠BAC
,它的顶点和边有什么特点?
圆周角:顶点在圆上,两边都与圆相交的角叫
圆周角.
归纳定义:
注意:(1)顶点在圆上,
(2)角的两边分别和圆相交.
小试牛刀:
1、下列各图中的角,其中为圆周角的是( )
2、图中有(
)个圆周角.
A.2
B.3
C.
4
D.5
B
C
三、探
观察下列操作,请你回答下列问题:
1、圆心和圆周角有几种位置关系?
环节一
(1)圆周角和圆心的位置关系的种类:
三、探
(2)猜想在上述三种情形下,在⊙O中,弧BC所对圆周角∠BAC和圆心角∠BOC有怎样的数量关系?并进行说理。
D
D
图1
图2
图3
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
(3)
圆心O在∠BAC的外部
环节二
1、通过以上的猜想论证你能用一句话来概括你的发现吗?先说给你的同桌听听。
三、探
2、你能用几何语言来描述这个定理吗?
?
一条弧所对的圆周角等于它所对圆心角的一半。
四、练:
3、已知三角形ABC为等边三角形,点O为圆心,,圆周角∠A=
,圆心角∠BOC=
60?
120?
4、已知:如图,在圆O中,∠BOC=50°,求∠W的大小
四、练
审题要仔细呦!
变式2
已知:在⊙O中,∠BOC=50°
如果BC=CE,求∠D的大小
变式1
在⊙O中,BC50°
,W是圆O上异于B、C的一点,求∠W的大小
user:
user:
由变式1、2的练习,你能得出什么结论?请说给你小组内的同学听,告诉他们,你的发现.
思考:
W’
在同圆或等圆中,同弧或等弧所对的圆周角相等,相等的圆周角所对的弧也相等.
圆周角定理推论1
总结归纳:
5、如图,AC是圆O的直径,
则∠ADC
=
,
∠ABC=
.
90°
90°
推论2:半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径.
四、练
6.
如图,在△ABC中,AB=AC,以AB为直径的圆交BC于D,交AC于E.
(1)
BD与CD的大小有什么关系?为什么?
A
B
C
D
E
∵AB是圆的直径,点D在圆上,
∴∠ADB=90°,
∴AD⊥BC,
又∵AB=AC,
∴△ABC为等腰三角形,∴BD=CD.
解:(1)BD=CD.
理由如下:连接AD,
(2)
求证:
.
(2)证明∵
△ABC为等腰三角形,AD⊥BC,
∴∠BAD=∠CAD.
∴
问题1:如图,在足球比赛场上,甲、乙,丙三名队员分别站在A、B,C三处,都能向对方球门MN进攻.且水平相当,此时,队友丁将球传给谁射门更好呢?为什么?传给乙和丙呢?(不考虑其他因素)
问题解决:
谈谈本节课你的收获和不足?
(知识,方法,体会)
五
结:
作业布置:
作业:课本P29
练习
T3
P31
习题24.3
T4
