沪科版八年级下册数学19.3 .2矩形的判定 课件(共22张PPT)
文档属性
| 名称 | 沪科版八年级下册数学19.3 .2矩形的判定 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 246.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 07:28:07 | ||
图片预览




文档简介
(共22张PPT)
19.3.2
矩形的判定
复习回顾
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
∟
矩形
四边形集合
平行四边形集合
矩形集合
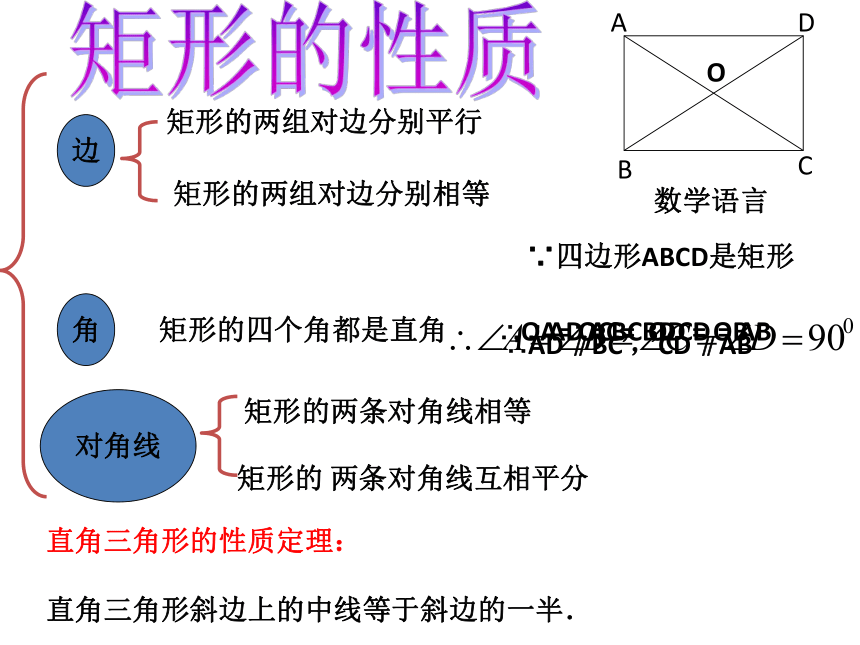
定义:有一个角是直角的平行四边形叫做矩形。
矩形的
两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形的两条对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD
=
BC
,CD
=
AB
∴AD
∥BC
,CD
∥AB
∴AC=
BD
A
B
C
D
O
∴OA=
OC
,OD
=
OB
矩形的性质
直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
工人师傅为了检验四边形窗框是否成矩形,可以有哪些方法?
想一想
A
B
C
D
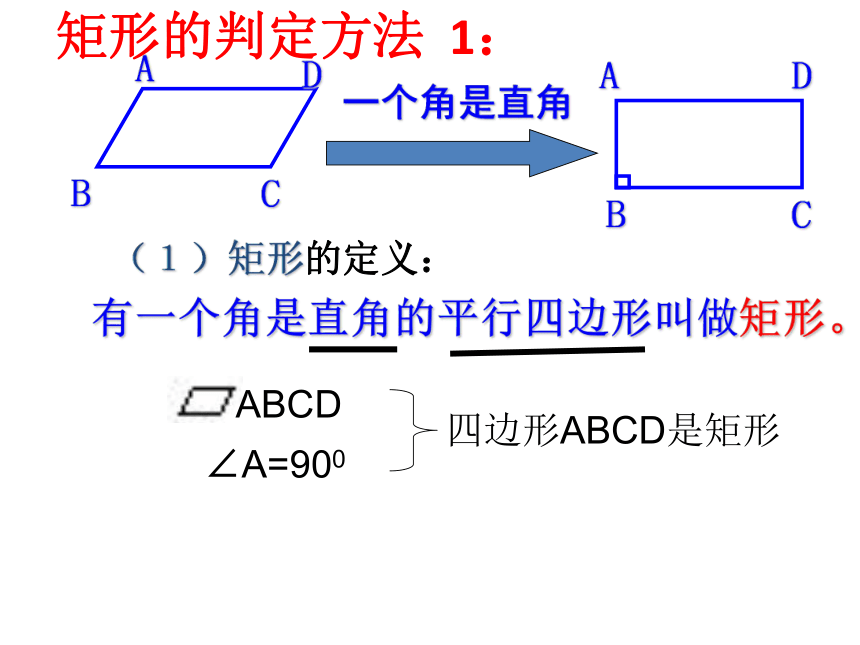
有一个角是直角的平行四边形叫做矩形。
A
B
C
D
(1)矩形的定义:
一个角是直角
矩形的判定方法
1:
ABCD
∠A=900
四边形ABCD是矩形
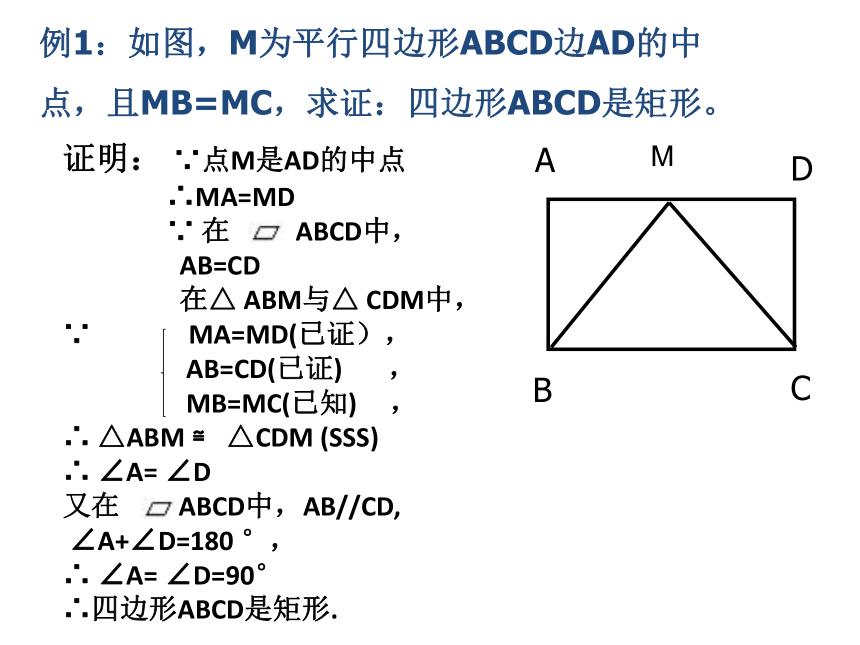
例1:如图,M为平行四边形ABCD边AD的中点,且MB=MC,求证:四边形ABCD是矩形。
A
B
C
D
M
证明:
∵点M是AD的中点
∴MA=MD
∵
在
ABCD中,
AB=CD
在△
ABM与△
CDM中,
∵
MA=MD(已证),
AB=CD(已证)
,
MB=MC(已知)
,
∴
△ABM
≌
△CDM
(SSS)
∴
∠A=
∠D
又在
ABCD中,AB//CD,
∠A+∠D=180
°,
∴
∠A=
∠D=90°
∴四边形ABCD是矩形.
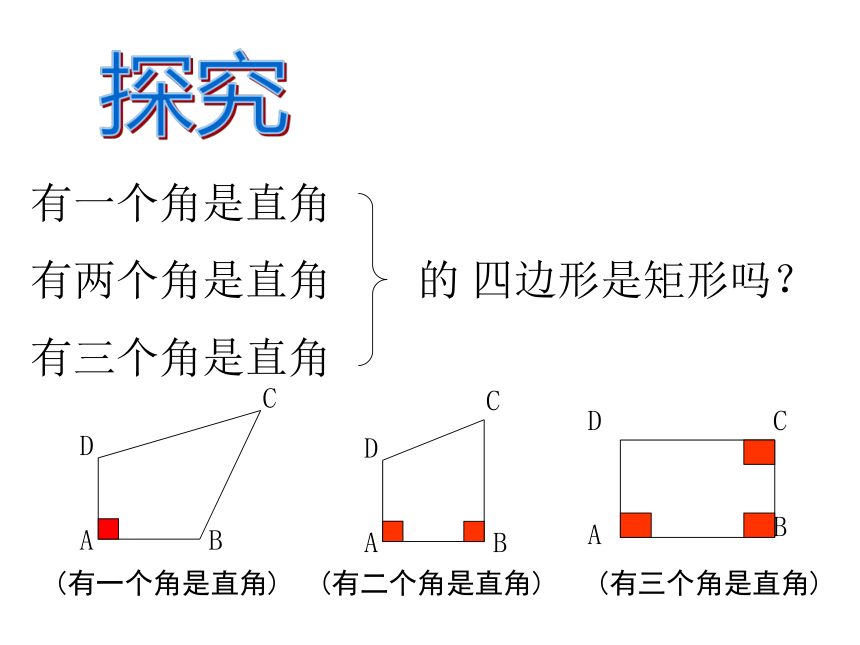
有一个角是直角
有两个角是直角
的
四边形是矩形吗?
有三个角是直角
探究
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
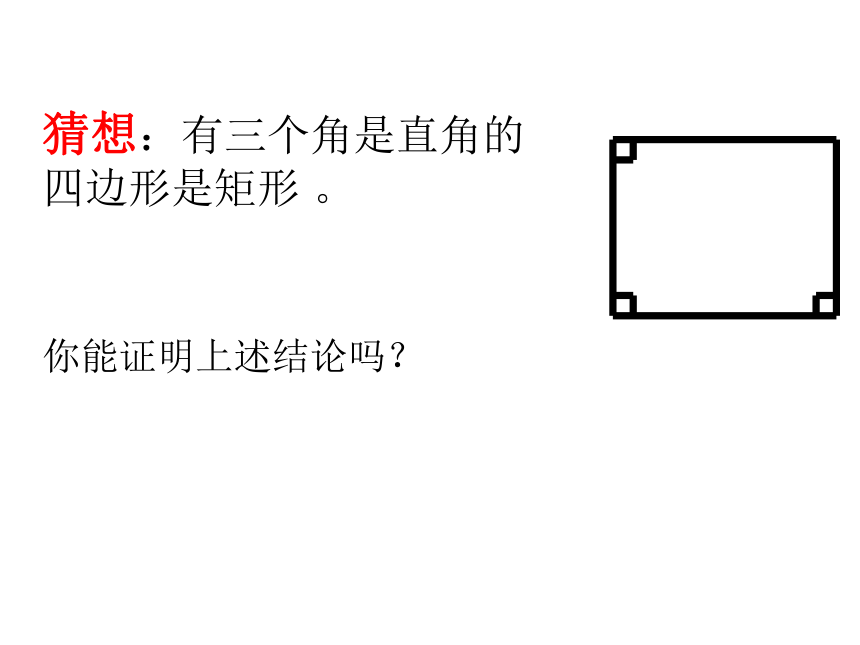
猜想:有三个角是直角的四边形是矩形
。
你能证明上述结论吗?
已知:在四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形。
A
B
C
D
∟
∟
∟
证明:∵
∠A=∠B=90°
∴
∠A+∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD是平行四边形
又∵
∠A=90°
∴四边形ABCD是矩形
矩形的判定方法2:
有三个角是直角的四边形是矩形
。
A
B
C
D
∵
∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
例2:
如果平行四边形四个内角的平分线能够围成一个四边形,那么这个四边形是矩形.
已知:如图,
???ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形
EFGH为矩形.
∴∠BGC=90°
同理可证∠AFB=∠AED=90°
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
???????????????????????????????????????
A
B
C
D
E
F
G
H
如果四边形ABCD的对角线AC=BD,这样的四边形是不是矩形?
A
B
C
D
AC=BD
A
B
C
D
AC=BD
都不是矩形
想一想
O
如果一个平行四边形的对角线变成相等呢?
A
B
C
D
将AC同时向两边拉长,使AC=BD
O
A
B
C
D
现在的
ABCD会是一个什么图形?
想一想
猜猜看:
工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形
。
对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
证明:
∵
AB=CD,
BC=DA,
AC=BD
∴
△ABC≌
△DCB(SSS)
∵
AB//CD
∴
∠ABC+∠DCB=180°
∴
∠ABC=∠DCB=90°
又∵
四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴
∠ABC=∠DCB
矩形的判定方法3:
对角线相等的平行四边形是矩形
。
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形。)
A
B
C
D
O
(或OA=OC=OB=OD)
例3:已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的点,AE=BF=CG=DH.
求证:四边形EFGH是矩形.
A
B
C
D
E
F
G
H
O
证明:
∵四边形ABCD为矩形
∴AC=BD
且AC与BD互相平分
∴OA=OB=OC=OD
∵AE=BF=CG=DH
∴OA-AE=OB-BF=OC-CG=OD-DH
即OE=OF=OG=OH
∴四边形EFGH为平行四边形
OE+OG=OF+OH
即EG=FH
∴四边形EFGH为矩形。
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形
。
(对角线相等且互相平分的四边形是矩形。)
有三个角是直角的四边形是矩形
。
方法1:
方法2:
方法3:
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(9)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
小结:矩形的判定方法
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形
。
(对角线相等且互相平分的四边形是矩形。)
有三个角是直角的四边形是矩形
。
方法1:
方法2:
方法3:
布置作业:
89页练习题
第1题和第2题。
19.3.2
矩形的判定
复习回顾
四边形
平行
四边形
两组对边
分别平行
一个角
是直角
∟
矩形
四边形集合
平行四边形集合
矩形集合
定义:有一个角是直角的平行四边形叫做矩形。
矩形的
两条对角线互相平分
矩形的两组对边分别相等
矩形的两组对边分别平行
矩形的四个角都是直角
矩形的两条对角线相等
边
对角线
角
数学语言
∵四边形ABCD是矩形
∴AD
=
BC
,CD
=
AB
∴AD
∥BC
,CD
∥AB
∴AC=
BD
A
B
C
D
O
∴OA=
OC
,OD
=
OB
矩形的性质
直角三角形的性质定理:
直角三角形斜边上的中线等于斜边的一半.
工人师傅为了检验四边形窗框是否成矩形,可以有哪些方法?
想一想
A
B
C
D
有一个角是直角的平行四边形叫做矩形。
A
B
C
D
(1)矩形的定义:
一个角是直角
矩形的判定方法
1:
ABCD
∠A=900
四边形ABCD是矩形
例1:如图,M为平行四边形ABCD边AD的中点,且MB=MC,求证:四边形ABCD是矩形。
A
B
C
D
M
证明:
∵点M是AD的中点
∴MA=MD
∵
在
ABCD中,
AB=CD
在△
ABM与△
CDM中,
∵
MA=MD(已证),
AB=CD(已证)
,
MB=MC(已知)
,
∴
△ABM
≌
△CDM
(SSS)
∴
∠A=
∠D
又在
ABCD中,AB//CD,
∠A+∠D=180
°,
∴
∠A=
∠D=90°
∴四边形ABCD是矩形.
有一个角是直角
有两个角是直角
的
四边形是矩形吗?
有三个角是直角
探究
A
B
D
C
(有一个角是直角)
A
B
D
C
(有二个角是直角)
A
B
D
C
(有三个角是直角)
猜想:有三个角是直角的四边形是矩形
。
你能证明上述结论吗?
已知:在四边形ABCD中,∠A=∠B=∠C=90°
求证:四边形ABCD是矩形。
A
B
C
D
∟
∟
∟
证明:∵
∠A=∠B=90°
∴
∠A+∠B=180°
∴AD∥BC
同理可证:AB∥CD
∴四边形ABCD是平行四边形
又∵
∠A=90°
∴四边形ABCD是矩形
矩形的判定方法2:
有三个角是直角的四边形是矩形
。
A
B
C
D
∵
∠A=∠B=∠C=90°
∴四边形ABCD是矩形
几何语言:
例2:
如果平行四边形四个内角的平分线能够围成一个四边形,那么这个四边形是矩形.
已知:如图,
???ABCD的四个内角的平分线分别相交于E、F、G、H,
求证:四边形
EFGH为矩形.
∴∠BGC=90°
同理可证∠AFB=∠AED=90°
∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵BG平分∠ABC,CG平分∠BCD
???????????????????????????????????????
A
B
C
D
E
F
G
H
如果四边形ABCD的对角线AC=BD,这样的四边形是不是矩形?
A
B
C
D
AC=BD
A
B
C
D
AC=BD
都不是矩形
想一想
O
如果一个平行四边形的对角线变成相等呢?
A
B
C
D
将AC同时向两边拉长,使AC=BD
O
A
B
C
D
现在的
ABCD会是一个什么图形?
想一想
猜猜看:
工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
猜想:对角线相等的平行四边形是矩形
。
对角线相等的平行四边形是矩形。
已知:平行四边形ABCD,AC=BD。
求证:四边形ABCD是矩形。
A
B
C
D
证明:
∵
AB=CD,
BC=DA,
AC=BD
∴
△ABC≌
△DCB(SSS)
∵
AB//CD
∴
∠ABC+∠DCB=180°
∴
∠ABC=∠DCB=90°
又∵
四边形ABCD是平行四边形
∴四边形ABCD是矩形
∴
∠ABC=∠DCB
矩形的判定方法3:
对角线相等的平行四边形是矩形
。
几何语言:
∵四边形ABCD是平行四边形
AC=BD
∴四边形ABCD是矩形
(对角线相等且互相平分的四边形是矩形。)
A
B
C
D
O
(或OA=OC=OB=OD)
例3:已知,如图.矩形ABCD的对角线AC、BD相交于点O,且E、F、G、H分别是AO、BO、CO、DO的点,AE=BF=CG=DH.
求证:四边形EFGH是矩形.
A
B
C
D
E
F
G
H
O
证明:
∵四边形ABCD为矩形
∴AC=BD
且AC与BD互相平分
∴OA=OB=OC=OD
∵AE=BF=CG=DH
∴OA-AE=OB-BF=OC-CG=OD-DH
即OE=OF=OG=OH
∴四边形EFGH为平行四边形
OE+OG=OF+OH
即EG=FH
∴四边形EFGH为矩形。
你能归纳矩形的几种判定方法吗?
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形
。
(对角线相等且互相平分的四边形是矩形。)
有三个角是直角的四边形是矩形
。
方法1:
方法2:
方法3:
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形;
(9)一组邻边垂直,一组对边平行且相等的四边形是矩形;
(8)一组对角互补的平行四边形是矩形;
(4)有三个角都相等的四边形是矩形;
X
X
X
X
小结:矩形的判定方法
有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形
。
(对角线相等且互相平分的四边形是矩形。)
有三个角是直角的四边形是矩形
。
方法1:
方法2:
方法3:
布置作业:
89页练习题
第1题和第2题。
