湘教版数学九年级下册:2.7 正多边形与圆 同步练习
文档属性
| 名称 | 湘教版数学九年级下册:2.7 正多边形与圆 同步练习 |  | |
| 格式 | zip | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 06:02:55 | ||
图片预览


文档简介
第2章 圆
2.7 正多边形与圆
1.
下面图形中,是正多边形的是(
).
A.
矩形
B.
菱形
C.
正方形
D.
等腰梯形
2.利用等分圆可以作正多边形,只利用直尺和圆规不能作出的多边形是(
)
A.正三角形
B.正方形
C.正六边形
D.正七边形
3.下列图形中,既是轴对称图形,又是中心对称图形的有(
)
①正三角形;②正方形;③正五边形;④正六边形;⑤线段;⑥圆;⑦菱形;⑧平行四边形.
A.3个
B.4个
C.5个
D.6个
4.
如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是(
)
A.
R2-r2=a2
B.
a=2Rsin36°
C.
a=2rtan36°
D.
r=Rcos36°
5.
小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为(
)
A.2cm
B.4cm
C.6cm
D.8cm
6.
已知等边三角形的内切圆半径、外接圆半径和高的比是(
)
A.1∶2∶
B.2∶3∶4
C.1∶∶2
D.1∶2∶3
7.
下列命题:①正多边形都有内切圆和外接圆,且这两个圆是同心圆;②各边相等的圆外切多边形是正多边形;③各角相等的圆内接多边形是正多边形;④正多边形既是轴对称图形又是中心对称图形;⑤正n边形的中心角是an=,且正多边形的中心角与其每一个外角相等.其中真命题有(
)
A.2个
B.3个
C.4个
D.5个
8.
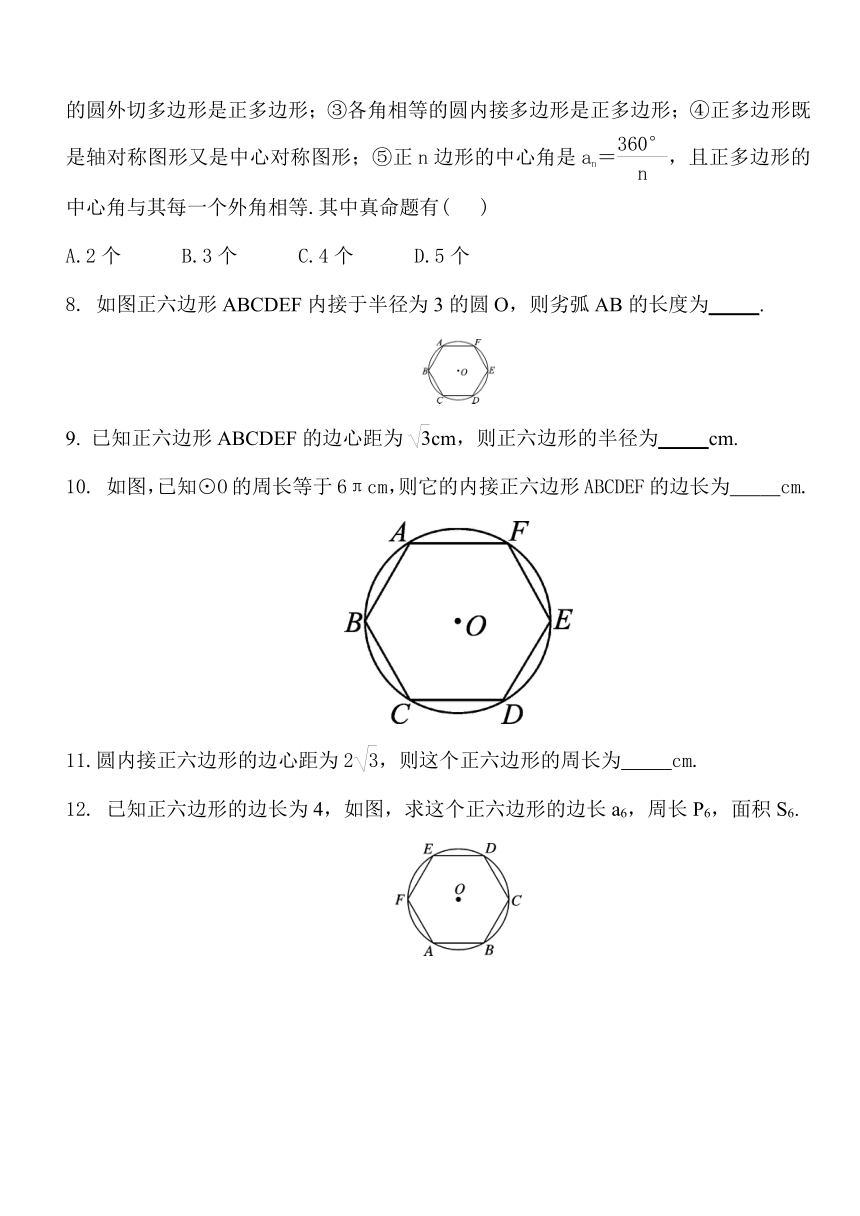
如图正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为
.
9.
已知正六边形ABCDEF的边心距为cm,则正六边形的半径为
cm.
10.
如图,已知⊙O的周长等于6πcm,则它的内接正六边形ABCDEF的边长为
cm.
11.圆内接正六边形的边心距为2,则这个正六边形的周长为
cm.
12.
已知正六边形的边长为4,如图,求这个正六边形的边长a6,周长P6,面积S6.
13.
如图所示,正五边形ABCDE的对角线AC和BE相交于点M,求证:
(1)
AC∥DE;
(2)
ME=AE.
14.
如图,点E、D分别是三角形ABC,正方形ABCM,正五边形ABCMN中以点C为顶点的相邻两边上的点,且BE=CD,DB交AE于P点.
(1)
求图①中,∠APD的度数;
(2)
图②中,∠APD的度数为________,图③中,∠APD的度数为________;
(3)
根据前面探索,你能否将本题推广到一般的正n边形中?若能,写出推广问题与结论;若不能,请说明理由.
答案:
1---7
CDCAB
DA
8.
π
9.
2
10.
3
11.
24
12.
解:过O作OG⊥AB于G,连接OA、OB,∴∠AOB==60°.∵OA=OB,∴△OAB是等边三角形,∴a6=4.P6=4×6=24.在Rt△OAG中,OA=4,AG=BG=2,∴OG==2,∴S6=×4×2×6=24.答:这个正六边形的边长是4,周长为24,面积为24.
13.
(1)
证明:∵正五边形,∴AB=CB,∴∠BAC=∠BCA.∵∠BAC+∠BCA+∠ABC=180°,∠ABC=108°,∴∠BAC=36°.∵∠EAC+∠BAC=∠EAB=108°,∴∠EAC=72°.∵∠AED=108°,∴∠EAC+∠AED=180°,∴AC∥DE.
(2)
证明:∵五边形ABCDE是正五边形,∴∠EAB=108°,EA=AB,∴∠BEA=∠ABE=36°,同理∠MAB=36°,∴∠EMA=72°,∠EAM=72°,∴EM=EA.
14.
解:(1)
正三角形ABC中,AB=BC,∠ABC=∠C=60°,又BE=CD,∴△ABE≌△BCD,∴∠BAE=∠CBD.∵∠ABD+∠DBC=60°,∴∠ABD+∠BAE=60°,即∠APD=60°;
(2)
90°;108°;
(3)能.推广的问题与结论为点E、D分别为正n边形中以C点为顶点的相邻两边上的点,且BE=CD,BD与AE交于点P,则∠APD的度数为.
2.7 正多边形与圆
1.
下面图形中,是正多边形的是(
).
A.
矩形
B.
菱形
C.
正方形
D.
等腰梯形
2.利用等分圆可以作正多边形,只利用直尺和圆规不能作出的多边形是(
)
A.正三角形
B.正方形
C.正六边形
D.正七边形
3.下列图形中,既是轴对称图形,又是中心对称图形的有(
)
①正三角形;②正方形;③正五边形;④正六边形;⑤线段;⑥圆;⑦菱形;⑧平行四边形.
A.3个
B.4个
C.5个
D.6个
4.
如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是(
)
A.
R2-r2=a2
B.
a=2Rsin36°
C.
a=2rtan36°
D.
r=Rcos36°
5.
小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为(
)
A.2cm
B.4cm
C.6cm
D.8cm
6.
已知等边三角形的内切圆半径、外接圆半径和高的比是(
)
A.1∶2∶
B.2∶3∶4
C.1∶∶2
D.1∶2∶3
7.
下列命题:①正多边形都有内切圆和外接圆,且这两个圆是同心圆;②各边相等的圆外切多边形是正多边形;③各角相等的圆内接多边形是正多边形;④正多边形既是轴对称图形又是中心对称图形;⑤正n边形的中心角是an=,且正多边形的中心角与其每一个外角相等.其中真命题有(
)
A.2个
B.3个
C.4个
D.5个
8.
如图正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为
.
9.
已知正六边形ABCDEF的边心距为cm,则正六边形的半径为
cm.
10.
如图,已知⊙O的周长等于6πcm,则它的内接正六边形ABCDEF的边长为
cm.
11.圆内接正六边形的边心距为2,则这个正六边形的周长为
cm.
12.
已知正六边形的边长为4,如图,求这个正六边形的边长a6,周长P6,面积S6.
13.
如图所示,正五边形ABCDE的对角线AC和BE相交于点M,求证:
(1)
AC∥DE;
(2)
ME=AE.
14.
如图,点E、D分别是三角形ABC,正方形ABCM,正五边形ABCMN中以点C为顶点的相邻两边上的点,且BE=CD,DB交AE于P点.
(1)
求图①中,∠APD的度数;
(2)
图②中,∠APD的度数为________,图③中,∠APD的度数为________;
(3)
根据前面探索,你能否将本题推广到一般的正n边形中?若能,写出推广问题与结论;若不能,请说明理由.
答案:
1---7
CDCAB
DA
8.
π
9.
2
10.
3
11.
24
12.
解:过O作OG⊥AB于G,连接OA、OB,∴∠AOB==60°.∵OA=OB,∴△OAB是等边三角形,∴a6=4.P6=4×6=24.在Rt△OAG中,OA=4,AG=BG=2,∴OG==2,∴S6=×4×2×6=24.答:这个正六边形的边长是4,周长为24,面积为24.
13.
(1)
证明:∵正五边形,∴AB=CB,∴∠BAC=∠BCA.∵∠BAC+∠BCA+∠ABC=180°,∠ABC=108°,∴∠BAC=36°.∵∠EAC+∠BAC=∠EAB=108°,∴∠EAC=72°.∵∠AED=108°,∴∠EAC+∠AED=180°,∴AC∥DE.
(2)
证明:∵五边形ABCDE是正五边形,∴∠EAB=108°,EA=AB,∴∠BEA=∠ABE=36°,同理∠MAB=36°,∴∠EMA=72°,∠EAM=72°,∴EM=EA.
14.
解:(1)
正三角形ABC中,AB=BC,∠ABC=∠C=60°,又BE=CD,∴△ABE≌△BCD,∴∠BAE=∠CBD.∵∠ABD+∠DBC=60°,∴∠ABD+∠BAE=60°,即∠APD=60°;
(2)
90°;108°;
(3)能.推广的问题与结论为点E、D分别为正n边形中以C点为顶点的相邻两边上的点,且BE=CD,BD与AE交于点P,则∠APD的度数为.
