人教版 2020年中考数学冲刺复习精讲——三角形与动点问题课件(共15张PPT)
文档属性
| 名称 | 人教版 2020年中考数学冲刺复习精讲——三角形与动点问题课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 23:42:56 | ||
图片预览


文档简介
(共15张PPT)
三角形与动点
专题
课前准备:双色笔+笔记本+作图工具
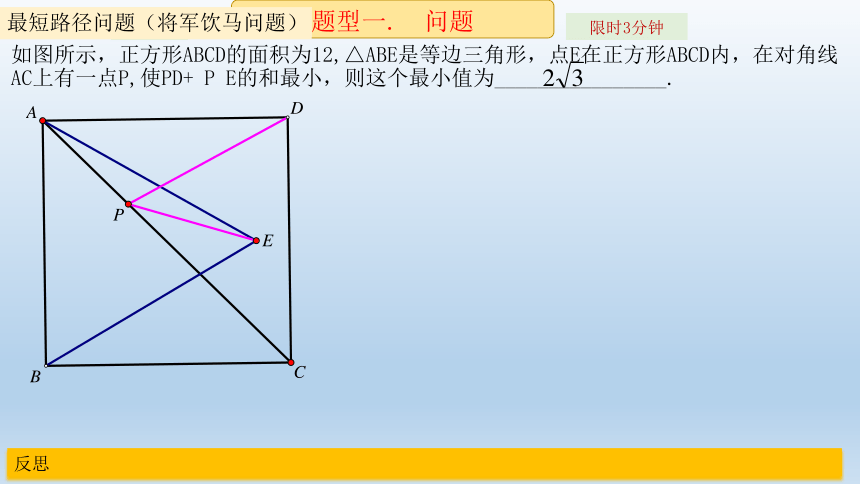
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+
P
E的和最小,则这个最小值为________________.
最短路径问题(将军饮马问题)
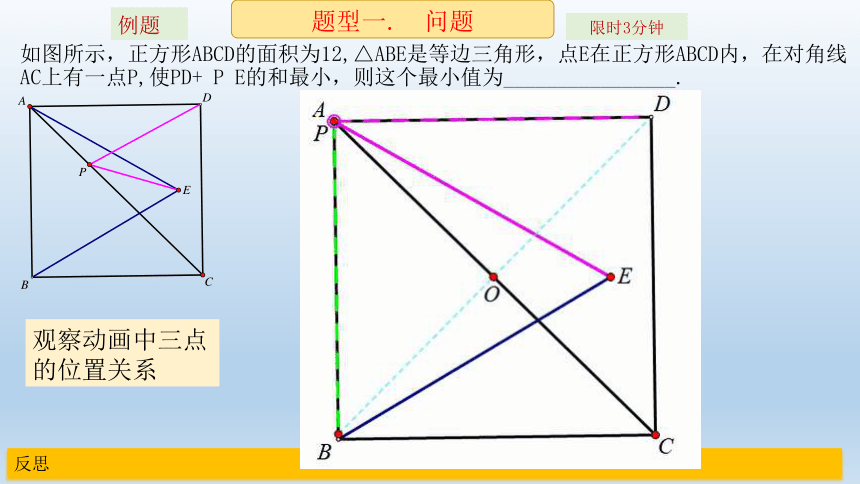
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+
P
E的和最小,则这个最小值为________________.
观察动画中三点的位置关系
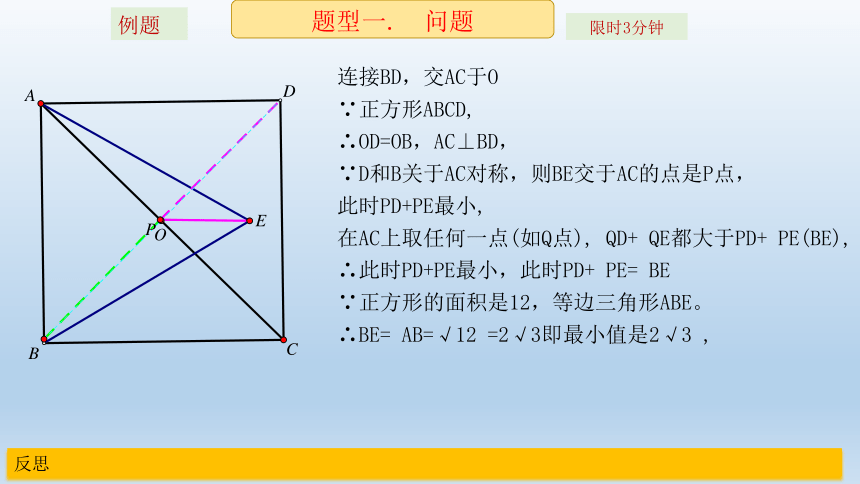
连接BD,交AC于O
∵正方形ABCD,
∴OD=OB,AC⊥BD,
∵D和B关于AC对称,则BE交于AC的点是P点,
此时PD+PE最小,
在AC上取任何一点(如Q点),
QD+
QE都大于PD+
PE(BE),
∴此时PD+PE最小,此时PD+
PE=
BE
∵正方形的面积是12,等边三角形ABE。
∴BE=
AB=√12
=2√3即最小值是2√3
,
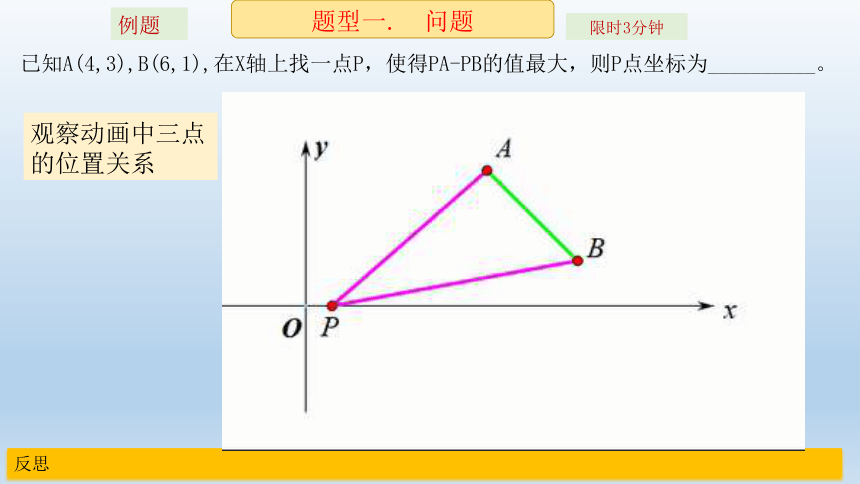
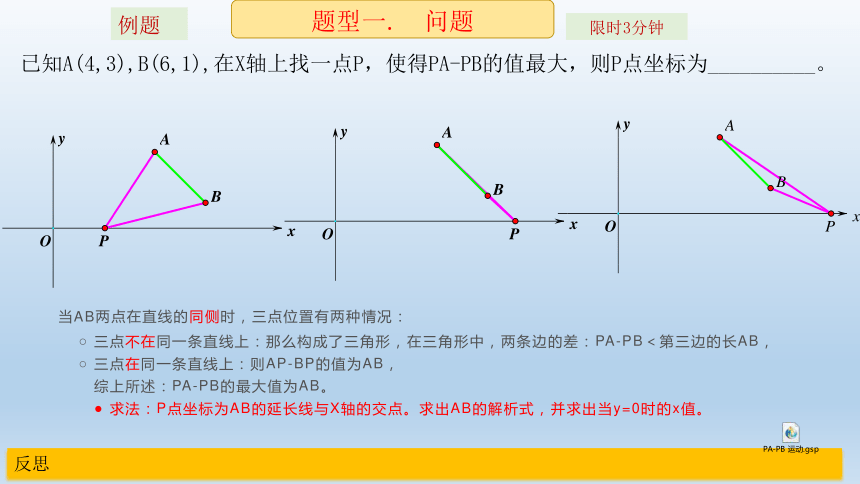
已知A(4,3),B(6,1),在X轴上找一点P,使得PA-PB的值最大,则P点坐标为__________。
观察动画中三点的位置关系
当AB两点在直线的同侧时,三点位置有两种情况:
三点不在同一条直线上:那么构成了三角形,在三角形中,两条边的差:PA-PB<第三边的长AB,
三点在同一条直线上:则AP-BP的值为AB,
综上所述:PA-PB的最大值为AB。
求法:P点坐标为AB的延长线与X轴的交点。求出AB的解析式,并求出当y=0时的x值。
已知A(4,3),B(6,1),在X轴上找一点P,使得PA-PB的值最大,则P点坐标为__________。
已知A(4,3),B(6,-1),在X轴上找一点P,使得PA-PB的值最大,则P点坐标为__________。
当AB两点在直线的同侧时,三点位置有两种情况:
三点不在同一条直线上:那么构成了三角形,在三角形中,两条边的差:PA-PB<第三边的长AB,
三点在同一条直线上:则AP-BP的值为AB,
综上所述:PA-PB的最大值为AB。
求法:P点坐标为AB的延长线与X轴的交点。求出AB的解析式,并求出当y=0时的x值。
当AB两点在直线的异侧时,通过做任一个点的对称点B‘,实现两点同侧。
求法:P点坐标为AB'的延长线与X轴的交点。求出AB'的解析式,并求出当y=0时的x值。
举一反三
如图,在等边△ABC中,AB=4
,点P是BC边上的动点,点P关于直线AB、AC的对称点分别为M、N,则线段MN长的取值范围是______.
观察动画
如图,在等边△ABC中,AB=4
,点P是BC边上的动点,点P关于直线AB、AC的对称点分别为M、N,则线段MN长的取值范围是______.
当点P为BC的中点时,MN最短,求出此时MN的长度;
01
当点P与点B
(或C)重合时,BN
(
或CM)最长,
求出此时BN
(
或CM)的长度。
02
由此即可得出MN的取值范围.
03
如图1,当点P为BC的中点时,MN最短。
此时E.F分别为AB、AC的中点,
PE=1/2AC,PF=1/2AB,
EF=
1/2BC
,
MN=
ME+
EF十FN=
PE+
EF+
PF=6;
如图2,当点P和点B(或点C)重合时,此时BN(或CM)最长。此时G(H)为AB(AC)的中点,
CG=
2√3(BH=
2√3),
CM=4√3
(BN=4√3).
故线段MN长的取值范围是6≤MN≤4√3.
由对称可得:AM=AP=AN
图1
图2
如图,在△ABC中,∠A=45°,∠B=60°,AB=4
,点P是BC边上的动点(不与B、C重合),点P关于直线AB、AC的对称点分别为M、N,则线段MN长的取值范围是______.
如图,在△ABC中,∠A=45°,∠B=60°,AB=4
,点P是BC边上的动点(不与B、C重合),点P关于直线AB、AC的对称点分别为M、N,则线段MN长的取值范围是______.
观察动画
由上一个题启发,你怎么解决这个问题?
你还能怎么做?
由题意可知,AM=AN=AP,
在RT△AMN中,
转化为求线段AP的范围
。
当AP⊥BC时,AP最小;
当点P与点B重合时,AP最长,但是P不与点B重合,所以AP<AB.
如图,在△ABC中,∠A=45°,∠B=60°,AB=4
,点P是BC边上的动点(不与B、C重合),点P关于直线AB、AC的对称点分别为M、N,则线段MN长的取值范围是______.
三角形与动点
专题
课前准备:双色笔+笔记本+作图工具
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+
P
E的和最小,则这个最小值为________________.
最短路径问题(将军饮马问题)
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+
P
E的和最小,则这个最小值为________________.
观察动画中三点的位置关系
连接BD,交AC于O
∵正方形ABCD,
∴OD=OB,AC⊥BD,
∵D和B关于AC对称,则BE交于AC的点是P点,
此时PD+PE最小,
在AC上取任何一点(如Q点),
QD+
QE都大于PD+
PE(BE),
∴此时PD+PE最小,此时PD+
PE=
BE
∵正方形的面积是12,等边三角形ABE。
∴BE=
AB=√12
=2√3即最小值是2√3
,
已知A(4,3),B(6,1),在X轴上找一点P,使得PA-PB的值最大,则P点坐标为__________。
观察动画中三点的位置关系
当AB两点在直线的同侧时,三点位置有两种情况:
三点不在同一条直线上:那么构成了三角形,在三角形中,两条边的差:PA-PB<第三边的长AB,
三点在同一条直线上:则AP-BP的值为AB,
综上所述:PA-PB的最大值为AB。
求法:P点坐标为AB的延长线与X轴的交点。求出AB的解析式,并求出当y=0时的x值。
已知A(4,3),B(6,1),在X轴上找一点P,使得PA-PB的值最大,则P点坐标为__________。
已知A(4,3),B(6,-1),在X轴上找一点P,使得PA-PB的值最大,则P点坐标为__________。
当AB两点在直线的同侧时,三点位置有两种情况:
三点不在同一条直线上:那么构成了三角形,在三角形中,两条边的差:PA-PB<第三边的长AB,
三点在同一条直线上:则AP-BP的值为AB,
综上所述:PA-PB的最大值为AB。
求法:P点坐标为AB的延长线与X轴的交点。求出AB的解析式,并求出当y=0时的x值。
当AB两点在直线的异侧时,通过做任一个点的对称点B‘,实现两点同侧。
求法:P点坐标为AB'的延长线与X轴的交点。求出AB'的解析式,并求出当y=0时的x值。
举一反三
如图,在等边△ABC中,AB=4
,点P是BC边上的动点,点P关于直线AB、AC的对称点分别为M、N,则线段MN长的取值范围是______.
观察动画
如图,在等边△ABC中,AB=4
,点P是BC边上的动点,点P关于直线AB、AC的对称点分别为M、N,则线段MN长的取值范围是______.
当点P为BC的中点时,MN最短,求出此时MN的长度;
01
当点P与点B
(或C)重合时,BN
(
或CM)最长,
求出此时BN
(
或CM)的长度。
02
由此即可得出MN的取值范围.
03
如图1,当点P为BC的中点时,MN最短。
此时E.F分别为AB、AC的中点,
PE=1/2AC,PF=1/2AB,
EF=
1/2BC
,
MN=
ME+
EF十FN=
PE+
EF+
PF=6;
如图2,当点P和点B(或点C)重合时,此时BN(或CM)最长。此时G(H)为AB(AC)的中点,
CG=
2√3(BH=
2√3),
CM=4√3
(BN=4√3).
故线段MN长的取值范围是6≤MN≤4√3.
由对称可得:AM=AP=AN
图1
图2
如图,在△ABC中,∠A=45°,∠B=60°,AB=4
,点P是BC边上的动点(不与B、C重合),点P关于直线AB、AC的对称点分别为M、N,则线段MN长的取值范围是______.
如图,在△ABC中,∠A=45°,∠B=60°,AB=4
,点P是BC边上的动点(不与B、C重合),点P关于直线AB、AC的对称点分别为M、N,则线段MN长的取值范围是______.
观察动画
由上一个题启发,你怎么解决这个问题?
你还能怎么做?
由题意可知,AM=AN=AP,
在RT△AMN中,
转化为求线段AP的范围
。
当AP⊥BC时,AP最小;
当点P与点B重合时,AP最长,但是P不与点B重合,所以AP<AB.
如图,在△ABC中,∠A=45°,∠B=60°,AB=4
,点P是BC边上的动点(不与B、C重合),点P关于直线AB、AC的对称点分别为M、N,则线段MN长的取值范围是______.
同课章节目录
