人教版八年级下册数学 17.2 勾股定理的逆定理 同步练习含答案
文档属性
| 名称 | 人教版八年级下册数学 17.2 勾股定理的逆定理 同步练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 203.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-10 23:27:44 | ||
图片预览



文档简介
17.2
勾股定理的逆定理
同步练习
一、选择题(每小题3分,共30分)
1.下列四组线段中,可以构成直角三角形的是(
)
A.4,5,6
B.2,3,4
C.,3,4
D.1,,3
2.适合下列条件的△ABC中,BC=a,AC=b,AB=c,直角三角形的个数为(
)
①②,∠A=45°;③∠A=320,∠B=58°;④⑤
A.2个
B.3个
C.4个
D.5个
3.若一个三角形的三边长的平方分别为:32,42,x2则此三角形是直角三角形的x2的值是(
)
A.42
B.52
C.7
D.52或7
4.在△ABC中,AB=,BC=,AC=,则(
)
A.∠A=90°
B.∠B=90°
C.∠C=90°
D.∠A=∠B
5.已知a,b,c为△ABC三边,且满足(a2-b2)(a2+b2-c2)=0,则它的形状为(
)
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
6.下列各组数是勾股数的是(
)
A.2,3,4
B.4,5,6
C.3.6,4.8,6
D.9,40,41
7.三角形三边长分别为8,15,17,则最短边上的高为(
)
A.8
B.15
C.16
D.17
8.已知a、b、c是三角形的三边长,如果满足(a﹣6)2+=0,则三角形的形状是(
)
A.底与腰不相等的等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
9.甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是(
)
A.北偏西30°
B.南偏西30°
C.南偏东60°
D.南偏西30°
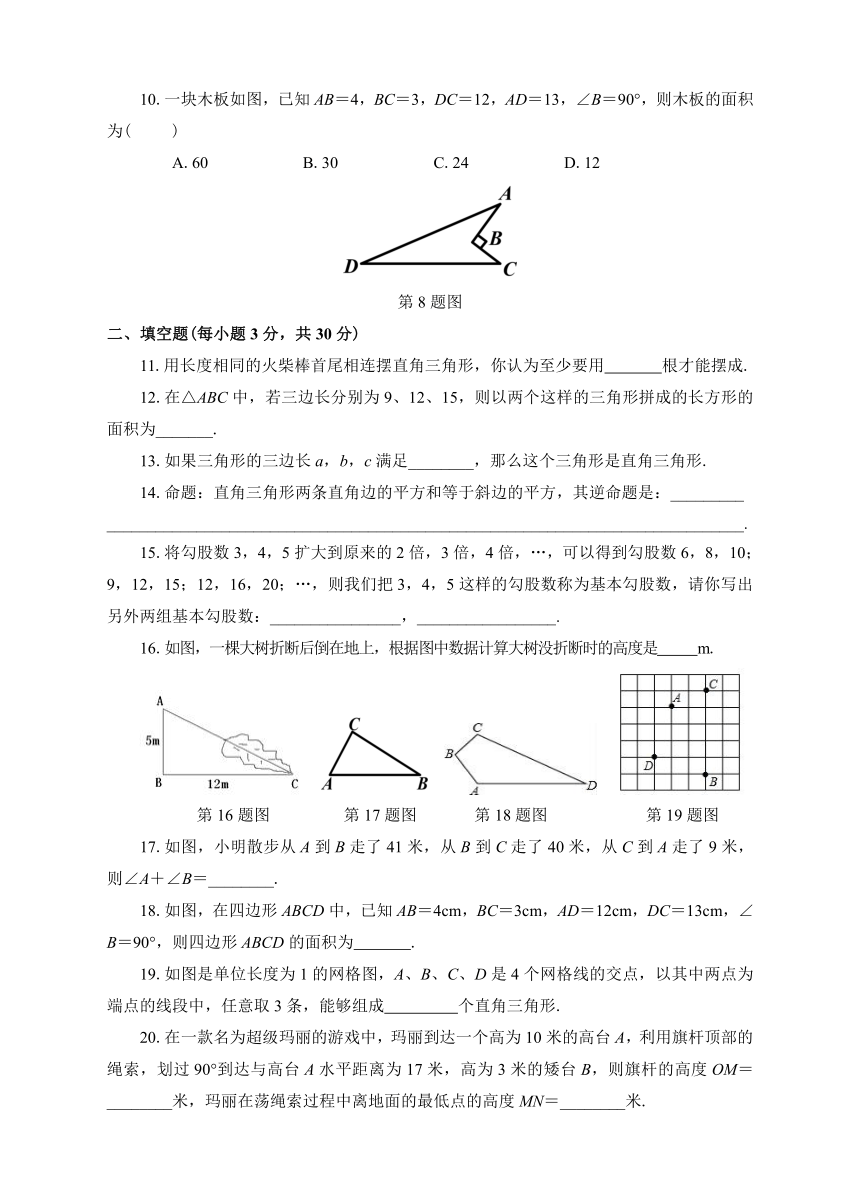
10.一块木板如图,已知AB=4,BC=3,DC=12,AD=13,∠B=90°,则木板的面积为(
)
A.60
B.30
C.24
D.12
第8题图
二、填空题(每小题3分,共30分)
11.用长度相同的火柴棒首尾相连摆直角三角形,你认为至少要用
根才能摆成.
12.在△ABC中,若三边长分别为9、12、15,则以两个这样的三角形拼成的长方形的面积为_______.
13.如果三角形的三边长a,b,c满足________,那么这个三角形是直角三角形.
14.命题:直角三角形两条直角边的平方和等于斜边的平方,其逆命题是:_________
______________________________________________________________________________.
15.将勾股数3,4,5扩大到原来的2倍,3倍,4倍,…,可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数,请你写出另外两组基本勾股数:________________,_________________.
16.如图,一棵大树折断后倒在地上,根据图中数据计算大树没折断时的高度是
m.
第16题图
第17题图
第18题图
第19题图
17.如图,小明散步从A到B走了41米,从B到C走了40米,从C到A走了9米,则∠A+∠B=________.
18.如图,在四边形ABCD中,已知AB=4cm,BC=3cm,AD=12cm,DC=13cm,∠B=90°,则四边形ABCD的面积为
.
19.如图是单位长度为1的网格图,A、B、C、D是4个网格线的交点,以其中两点为端点的线段中,任意取3条,能够组成
个直角三角形.
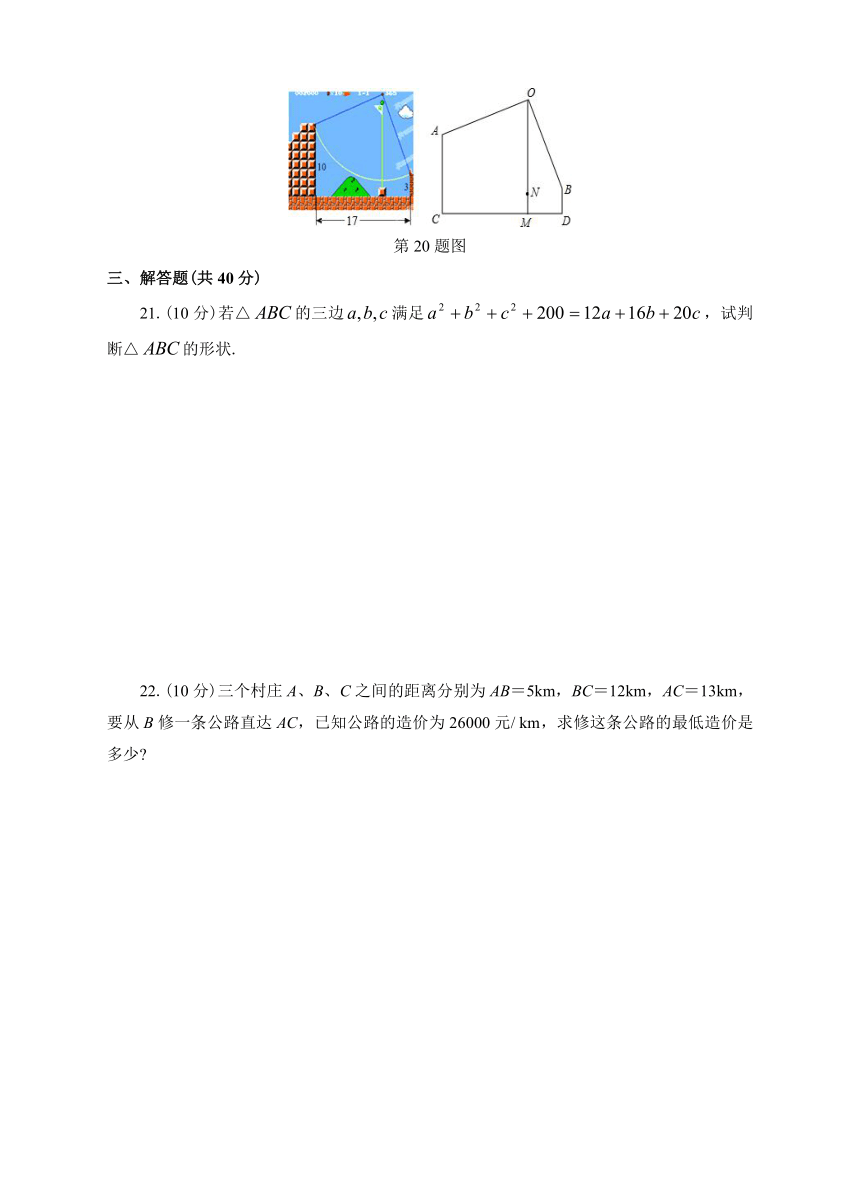
20.在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,则旗杆的高度OM=________米,玛丽在荡绳索过程中离地面的最低点的高度MN=________米.
第20题图
三、解答题(共40分)
21.(10分)若△的三边满足,试判断△的形状.
22.(10分)三个村庄A、B、C之间的距离分别为AB=5km,BC=12km,AC=13km,要从B修一条公路直达AC,已知公路的造价为26000元/
km,求修这条公路的最低造价是多少?
23.(10分)有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?
24.(10分)如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
(1)求DC和AB的长;
(2)证明:∠ACB=90°.
参考答案
1.C
2.A
3.D
【解析】此题要考虑两种情况:x是斜边或4是斜边.根据勾股定理,即“两条直角边的平方等于斜边的平方”进行求解.
当x是斜边时,则x2=9+16=25;
当4是斜边时,则x2=16-9=7
故选D
4.A
【解析】根据题目提供的三角形的三边长,计算它们的平方,满足a2+b2=c2,哪一个是斜边,其所对的角就是直角.
解:∵AB2=()2=2,BC2=()2=5,AC2=()2=3,
∴AB2+AC2=BC2,
∴BC边是斜边,
∴∠A=90°.
故选A.
5.D.
【解析】因为a,b,c为三角形三边,根据(a2-b2)(a2+b2-c2)=0,可找到这三边的数量关系.∵(a2-b2)(a2+b2-c2)=0,∴a=b或a2+b2=c2.当只有a=b成立时,是等腰三角形.当只有第二个条件成立时:是直角三角形.当两个条件同时成立时:是等腰直角三角形.故正确的选项是D.
6.D
【解析】利用勾股数的定义进行判断.A选项,42≠22+32,故2,3,4不是勾股数;B选项,62≠42+52,故4,5,6不是勾股数;C选项,3.6,4.8不是正整数,故不是勾股数;D选项,三数均为正整数,且412=92+402,故9,40,41是勾股数.故选D.
7.B.
【解析】∵三角形的三边长分别为8,15,17,符合勾股定理的逆定理152+82=172,
∴此三角形为直角三角形,则8为直角三角形的最短边,并且是直角边,
那么这个三角形的最短边上的高为15.
故选B.
8.D
【解析】首先根据绝对值,平方数与算术平方根的非负性,求出a,b,c的值,在根据勾股定理的逆定理判断其形状是直角三角形.
解:∵(a﹣6)2≥0,≥0,|c﹣10|≥0,
又∵(a﹣b)2+=0,
∴a﹣6=0,b﹣8=0,c﹣10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴是直角三角形.
故选D.
9.C
【解析】甲的路程:40×15=600米,
乙的路程:20×40=800米,
∵6002+8002=10002,
∴甲和乙两艘轮船的行驶路线呈垂直关系,
∵甲客轮沿着北偏东30°,
∴乙客轮的航行方向可能是南偏东60°,
故选:C.
10.C
【解析】连接AC,在Rt△ABC中,AC2=AB2+BC2=42+32=52,AC=5.在△ADC中,AC2+DC2=52+122=132=AD2,则△ADC是直角三角形,所以木板的面积.
11.12.
【解析】直角三角形的三边长为3,4,5时,三角形的周长最小,3+4+5=12,故答案为:12.
12.108
【解析】∵在△ABC中,三条边的长度分别为9、12、15,92+122=152,
∴△ABC是直角三角形,
∴用两个这样的三角形所拼成的长方形的面积是2××9×12=108
13.a2+b2=c2
【解析】根据勾股定理的逆定理求得
14.如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形为直角三角形.
【解析】直角三角形两条直角边的平方和等于斜边的平方,其逆命题是:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形为直角三角形.
故答案为:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形为直角三角形.
15.5,12,13;7,24,25
【解析】答案不唯一,只要满足题意即可.
16.18
【解析】在Rt△ABC中,由AB=5,BC=12,根据勾股定理可得AC===13m,即折断树的高度为13m;因此可得大树的高度=13+5=18m.
17.90°
【解析】∵AC2+BC2=92+402=1681,而AB2=412=1681,△ABC为直角三角形∠C=90°,∴∠A+∠B=90°
18.36cm2
【解析】连接AC,先根据直角三角形的性质得到AC边的长度,再根据三角形ACD中的三边关系可判定△ACD是Rt△,把四边形分成两个直角三角形即可求得面积.
解:连接AC,
∵∠B=90°
∴AC2=AB2+BC2=16+9=25,
∵AD2=144,DC2=169,
∴AC2+AD2=DC2,
∴CA⊥AD
∴S四ABCD=S△ABC+S△ACD=×3×4+×12×5=36cm2.
19.2
【解析】根据小正方形的边长可分别求,,,,,,根据勾股定理的逆定理,由知△ADB是直角三角形,由知△ABC是直角三角形.共2个.
20.15;2
【解析】首先得出△AOE≌△OBF(AAS),进而得出CD的长,进而求出OM,MN的长即可.
解:作AE⊥OM,BF⊥OM,
∵∠AOE+∠BOF=∠BOF+∠OBF=90°
∴∠AOE=∠OBF
在△AOE和△OBF中,
,
∴△AOE≌△OBF(AAS),
∴OE=BF,AE=OF
即OE+OF=AE+BF=CD=17(m)
∵EF=EM﹣FM=AC﹣BD=10﹣3=7(m),
∴2EO+EF=17,
则2×EO=10,
所以OE=5m,OF=12m,
所以OM=OF+FM=15m
又因为由勾股定理得ON=OA=13,
所以MN=15﹣13=2(m).
答:旗杆的高度OM为15米,玛丽在荡绳索过程中离地面的最低点的高度MN为2米.
21.△ABC是直角三角形.
【解析】本题通过对式子的整理得到a、b、c的值,根据勾股定理的逆定理判定三角形的形状.
解:∵a2+b2+c2+200=12a+16b+20c,
∴(a-6)2+(b-8)2+(c-10)2=0,
∴(a-6)=0,(b-8)=0,(c-10)=0,
∴a=6,b=8,c=10,
∵62+82=102,
∴a2+b2=c2,
∴△ABC是直角三角形.
22.120000元.
【解析】由=169,=169,得到∠ABC=90°,从而确定出最短距离,然后利用面积相等求得BD的长,最终求得最低造价.
试题解析:∵==169,=169,∴=,∴∠ABC=90°,当BD⊥AC时BD最短,造价最低,∵S△ABC=AB?BC=AC?BD,∴BD==km,×26000=120000元.
答:最低造价为120000元.
23.是,理由见解析.
【解析】先在△ABC中,由∠B=90°,可得△ABC为直角三角形;根据勾股定理得出AC2=AB2+BC2=8,那么AD2+AC2=9=DC2,由勾股定理的逆定理可得△ACD也为直角三角形.
解:都是直角三角形.理由如下:
连结AC.
在△ABC中,∵∠B=90°,
∴△ABC为直角三角形;
∴AC2=AB2+BC2=8,
又∵AD2+AC2=1+8=9,而DC2=9,
∴AC2+AD2=DC2,
∴△ACD也为直角三角形.
24.(1)CD=12;AB=25;(2)略
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
勾股定理的逆定理
同步练习
一、选择题(每小题3分,共30分)
1.下列四组线段中,可以构成直角三角形的是(
)
A.4,5,6
B.2,3,4
C.,3,4
D.1,,3
2.适合下列条件的△ABC中,BC=a,AC=b,AB=c,直角三角形的个数为(
)
①②,∠A=45°;③∠A=320,∠B=58°;④⑤
A.2个
B.3个
C.4个
D.5个
3.若一个三角形的三边长的平方分别为:32,42,x2则此三角形是直角三角形的x2的值是(
)
A.42
B.52
C.7
D.52或7
4.在△ABC中,AB=,BC=,AC=,则(
)
A.∠A=90°
B.∠B=90°
C.∠C=90°
D.∠A=∠B
5.已知a,b,c为△ABC三边,且满足(a2-b2)(a2+b2-c2)=0,则它的形状为(
)
A.直角三角形
B.等腰三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
6.下列各组数是勾股数的是(
)
A.2,3,4
B.4,5,6
C.3.6,4.8,6
D.9,40,41
7.三角形三边长分别为8,15,17,则最短边上的高为(
)
A.8
B.15
C.16
D.17
8.已知a、b、c是三角形的三边长,如果满足(a﹣6)2+=0,则三角形的形状是(
)
A.底与腰不相等的等腰三角形
B.等边三角形
C.钝角三角形
D.直角三角形
9.甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是(
)
A.北偏西30°
B.南偏西30°
C.南偏东60°
D.南偏西30°
10.一块木板如图,已知AB=4,BC=3,DC=12,AD=13,∠B=90°,则木板的面积为(
)
A.60
B.30
C.24
D.12
第8题图
二、填空题(每小题3分,共30分)
11.用长度相同的火柴棒首尾相连摆直角三角形,你认为至少要用
根才能摆成.
12.在△ABC中,若三边长分别为9、12、15,则以两个这样的三角形拼成的长方形的面积为_______.
13.如果三角形的三边长a,b,c满足________,那么这个三角形是直角三角形.
14.命题:直角三角形两条直角边的平方和等于斜边的平方,其逆命题是:_________
______________________________________________________________________________.
15.将勾股数3,4,5扩大到原来的2倍,3倍,4倍,…,可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数,请你写出另外两组基本勾股数:________________,_________________.
16.如图,一棵大树折断后倒在地上,根据图中数据计算大树没折断时的高度是
m.
第16题图
第17题图
第18题图
第19题图
17.如图,小明散步从A到B走了41米,从B到C走了40米,从C到A走了9米,则∠A+∠B=________.
18.如图,在四边形ABCD中,已知AB=4cm,BC=3cm,AD=12cm,DC=13cm,∠B=90°,则四边形ABCD的面积为
.
19.如图是单位长度为1的网格图,A、B、C、D是4个网格线的交点,以其中两点为端点的线段中,任意取3条,能够组成
个直角三角形.
20.在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,则旗杆的高度OM=________米,玛丽在荡绳索过程中离地面的最低点的高度MN=________米.
第20题图
三、解答题(共40分)
21.(10分)若△的三边满足,试判断△的形状.
22.(10分)三个村庄A、B、C之间的距离分别为AB=5km,BC=12km,AC=13km,要从B修一条公路直达AC,已知公路的造价为26000元/
km,求修这条公路的最低造价是多少?
23.(10分)有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?
24.(10分)如图,已知在△ABC中,CD⊥AB于D,AC=20,BC=15,DB=9.
(1)求DC和AB的长;
(2)证明:∠ACB=90°.
参考答案
1.C
2.A
3.D
【解析】此题要考虑两种情况:x是斜边或4是斜边.根据勾股定理,即“两条直角边的平方等于斜边的平方”进行求解.
当x是斜边时,则x2=9+16=25;
当4是斜边时,则x2=16-9=7
故选D
4.A
【解析】根据题目提供的三角形的三边长,计算它们的平方,满足a2+b2=c2,哪一个是斜边,其所对的角就是直角.
解:∵AB2=()2=2,BC2=()2=5,AC2=()2=3,
∴AB2+AC2=BC2,
∴BC边是斜边,
∴∠A=90°.
故选A.
5.D.
【解析】因为a,b,c为三角形三边,根据(a2-b2)(a2+b2-c2)=0,可找到这三边的数量关系.∵(a2-b2)(a2+b2-c2)=0,∴a=b或a2+b2=c2.当只有a=b成立时,是等腰三角形.当只有第二个条件成立时:是直角三角形.当两个条件同时成立时:是等腰直角三角形.故正确的选项是D.
6.D
【解析】利用勾股数的定义进行判断.A选项,42≠22+32,故2,3,4不是勾股数;B选项,62≠42+52,故4,5,6不是勾股数;C选项,3.6,4.8不是正整数,故不是勾股数;D选项,三数均为正整数,且412=92+402,故9,40,41是勾股数.故选D.
7.B.
【解析】∵三角形的三边长分别为8,15,17,符合勾股定理的逆定理152+82=172,
∴此三角形为直角三角形,则8为直角三角形的最短边,并且是直角边,
那么这个三角形的最短边上的高为15.
故选B.
8.D
【解析】首先根据绝对值,平方数与算术平方根的非负性,求出a,b,c的值,在根据勾股定理的逆定理判断其形状是直角三角形.
解:∵(a﹣6)2≥0,≥0,|c﹣10|≥0,
又∵(a﹣b)2+=0,
∴a﹣6=0,b﹣8=0,c﹣10=0,
解得:a=6,b=8,c=10,
∵62+82=36+64=100=102,
∴是直角三角形.
故选D.
9.C
【解析】甲的路程:40×15=600米,
乙的路程:20×40=800米,
∵6002+8002=10002,
∴甲和乙两艘轮船的行驶路线呈垂直关系,
∵甲客轮沿着北偏东30°,
∴乙客轮的航行方向可能是南偏东60°,
故选:C.
10.C
【解析】连接AC,在Rt△ABC中,AC2=AB2+BC2=42+32=52,AC=5.在△ADC中,AC2+DC2=52+122=132=AD2,则△ADC是直角三角形,所以木板的面积.
11.12.
【解析】直角三角形的三边长为3,4,5时,三角形的周长最小,3+4+5=12,故答案为:12.
12.108
【解析】∵在△ABC中,三条边的长度分别为9、12、15,92+122=152,
∴△ABC是直角三角形,
∴用两个这样的三角形所拼成的长方形的面积是2××9×12=108
13.a2+b2=c2
【解析】根据勾股定理的逆定理求得
14.如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形为直角三角形.
【解析】直角三角形两条直角边的平方和等于斜边的平方,其逆命题是:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形为直角三角形.
故答案为:如果一个三角形的两边的平方和等于第三边的平方,那么这个三角形为直角三角形.
15.5,12,13;7,24,25
【解析】答案不唯一,只要满足题意即可.
16.18
【解析】在Rt△ABC中,由AB=5,BC=12,根据勾股定理可得AC===13m,即折断树的高度为13m;因此可得大树的高度=13+5=18m.
17.90°
【解析】∵AC2+BC2=92+402=1681,而AB2=412=1681,△ABC为直角三角形∠C=90°,∴∠A+∠B=90°
18.36cm2
【解析】连接AC,先根据直角三角形的性质得到AC边的长度,再根据三角形ACD中的三边关系可判定△ACD是Rt△,把四边形分成两个直角三角形即可求得面积.
解:连接AC,
∵∠B=90°
∴AC2=AB2+BC2=16+9=25,
∵AD2=144,DC2=169,
∴AC2+AD2=DC2,
∴CA⊥AD
∴S四ABCD=S△ABC+S△ACD=×3×4+×12×5=36cm2.
19.2
【解析】根据小正方形的边长可分别求,,,,,,根据勾股定理的逆定理,由知△ADB是直角三角形,由知△ABC是直角三角形.共2个.
20.15;2
【解析】首先得出△AOE≌△OBF(AAS),进而得出CD的长,进而求出OM,MN的长即可.
解:作AE⊥OM,BF⊥OM,
∵∠AOE+∠BOF=∠BOF+∠OBF=90°
∴∠AOE=∠OBF
在△AOE和△OBF中,
,
∴△AOE≌△OBF(AAS),
∴OE=BF,AE=OF
即OE+OF=AE+BF=CD=17(m)
∵EF=EM﹣FM=AC﹣BD=10﹣3=7(m),
∴2EO+EF=17,
则2×EO=10,
所以OE=5m,OF=12m,
所以OM=OF+FM=15m
又因为由勾股定理得ON=OA=13,
所以MN=15﹣13=2(m).
答:旗杆的高度OM为15米,玛丽在荡绳索过程中离地面的最低点的高度MN为2米.
21.△ABC是直角三角形.
【解析】本题通过对式子的整理得到a、b、c的值,根据勾股定理的逆定理判定三角形的形状.
解:∵a2+b2+c2+200=12a+16b+20c,
∴(a-6)2+(b-8)2+(c-10)2=0,
∴(a-6)=0,(b-8)=0,(c-10)=0,
∴a=6,b=8,c=10,
∵62+82=102,
∴a2+b2=c2,
∴△ABC是直角三角形.
22.120000元.
【解析】由=169,=169,得到∠ABC=90°,从而确定出最短距离,然后利用面积相等求得BD的长,最终求得最低造价.
试题解析:∵==169,=169,∴=,∴∠ABC=90°,当BD⊥AC时BD最短,造价最低,∵S△ABC=AB?BC=AC?BD,∴BD==km,×26000=120000元.
答:最低造价为120000元.
23.是,理由见解析.
【解析】先在△ABC中,由∠B=90°,可得△ABC为直角三角形;根据勾股定理得出AC2=AB2+BC2=8,那么AD2+AC2=9=DC2,由勾股定理的逆定理可得△ACD也为直角三角形.
解:都是直角三角形.理由如下:
连结AC.
在△ABC中,∵∠B=90°,
∴△ABC为直角三角形;
∴AC2=AB2+BC2=8,
又∵AD2+AC2=1+8=9,而DC2=9,
∴AC2+AD2=DC2,
∴△ACD也为直角三角形.
24.(1)CD=12;AB=25;(2)略
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
