华师大版七年级数学下册 第9章《多边形》检测卷(无答案)
文档属性
| 名称 | 华师大版七年级数学下册 第9章《多边形》检测卷(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 127.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 09:17:41 | ||
图片预览

文档简介
七年级数学第9章《多边形》检测卷
(满分150分,时间120分
)
A.基础闯关(90分)
一、选择题(每道题只有一个正确答案,每小题4分,共计28分)
1.已知某n边形的外角和恰好等于它的内角和的2倍,则n=(
)
A.
3??????
B.
4???????
C.
5????????
D.
6
2.如图,为了估计池塘岸边A,B两点间的距离,小彤同学在池塘一侧
选取一点O,测得OA=11米,OB=6米,则A,B间的距离可能是(?
)
3米??????
B.
4米??????C.
5米???????D.
6米
3.等腰三角形的一个底角为63?
,则它的顶角为(??
)
A.
60???????
B.
58??????
C.
56????????
D.
54?
4.在下列各图中,分别画出了△ABC中BC边上的高AD,其中正确的是(??
)
5.已知等腰△ABC的两边长分别为3cm和7cm,则△ABC的周长为(
)
A.
13cm?????
B.
17cm??????C.
13cm或17cm?????D.不能确定
6.以下几种多边形中,不能用于铺设无缝地板的是(
)
A.正三角形
B.正四边形
C.正五边形
D.正六边形
7.如图,一副三角板叠在一起如图所示放置,最小锐角
的点D恰好放在等腰直角三角板的斜边AB上,BC与DE
交于点M,如果∠ADF=96°,那么∠BME为(
).
A.101°???
B.
100°??
C.
99°???
D.
98°
二、填空题(每小题4分,共12分)
8.自行车的车身为三角形结构,这样做根据的数学道理是___________________;
9.用三种不同的正多边形地砖铺满地面,若其中有正方形,正六边形,则另一个为正
边形;
10.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,
其摆放方式如图所示,则∠AOB等于________度.
三、解答题(50分)
11.(8分)已知:某正多边形的一个外角是它相邻的内角的
,求这个多边形的边数.
12.(8分)等腰△ABC中,腰AB=AC,BD是AC边上的中线,已知△ABD的周长比△BCD的周长大7cm,且腰长是底边长的2倍,求△ABC的周长.
13.(8分)小华从点A出发向前走8米,向右转36?然后继续向前走8米,再向右转36?,他以同样的方法继续走下去,他能回到点A吗?若能,当他走回到点A时共走多少米?若不能,写出理由。
14.(8分)如果同时选用边长相等的正三角形和正方形(数量自定)密铺地板,可以怎样搭配?请画出两种密铺示意图。
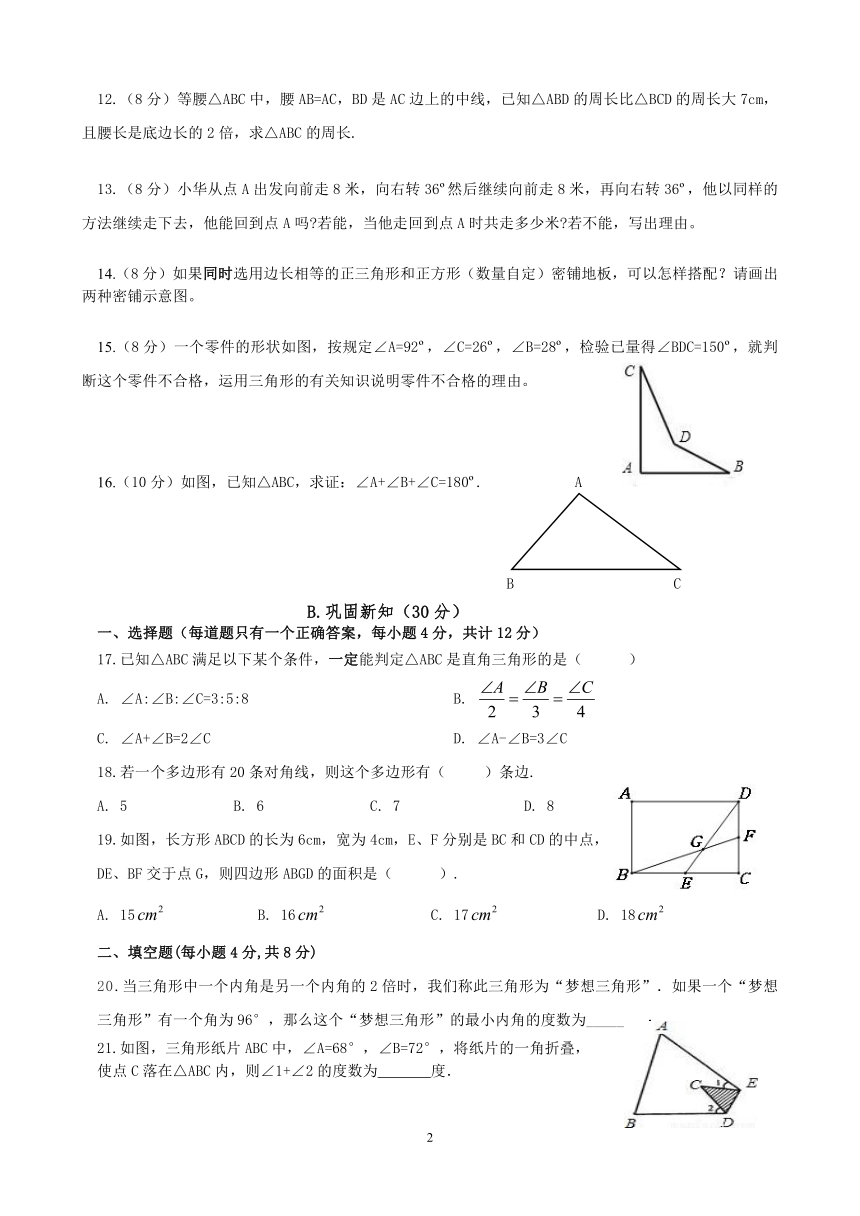
15.(8分)一个零件的形状如图,按规定∠A=92?,∠C=26?,∠B=28?,检验已量得∠BDC=150?,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
16.(10分)如图,已知△ABC,求证:∠A+∠B+∠C=180?.
A
B
C
B.巩固新知(30分)
一、选择题(每道题只有一个正确答案,每小题4分,共计12分)
17.已知△ABC满足以下某个条件,一定能判定△ABC是直角三角形的是(
)
A.
∠A:∠B:∠C=3:5:8
B.
C.
∠A+∠B=2∠C
D.
∠A-∠B=3∠C
18.若一个多边形有20条对角线,则这个多边形有(??
)条边.
A.
5???????B.
6???????C.
7????????D.
8
19.如图,长方形ABCD的长为6cm,宽为4cm,E、F分别是BC和CD的中点,
DE、BF交于点G,则四边形ABGD的面积是(??
).
A.
15
B.
16
C.
17
D.
18
二、填空题(每小题4分,共8分)
20.当三角形中一个内角是另一个内角的2倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为96°,那么这个“梦想三角形”的最小内角的度数为________;
21.如图,三角形纸片ABC中,∠A=68°,∠B=72°,将纸片的一角折叠,
使点C落在△ABC内,则∠1+∠2的度数为
度.
三、解答题(10分)
22.(10分)如图,△ABC中,CE平分∠ACB,CD⊥AB于D,DF⊥CE交CE于F,
若∠A=50?,∠B=80?,求∠CDF的度数;
求证:∠DCE=
.
C.能力提升(16分)
23.(4分)右图8×8的网格图中,△ABC的三个顶点均在网格
交点处,如果每个小方格的面积是1,那么:
△ABC的面积是________;
若边AB长5,则AB边上的高CD=______;
24.(12分)“转化”是数学中的一种重要思想。
(1)五角星图1的点A向下移动到BE的下方得到星形图2,请你根据学过的知识求出图2中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图2中星形截去∠A,如图3,请你求出∠B+∠C+∠D+∠E+∠F+∠G的度数;
(3)若再对图3中星形截去∠D,如图4,你能由题(2)中所得的方法或规律,猜想图4中的∠B+∠C+∠M+∠N+∠E+∠F+∠G的度数吗?(只要写出结论,不需要写出解题过程)
核心素养(14分)
25.(1)如图Ⅰ,在△ABC中,点D是两条内角平分线的交点,点E是两条外角平分线的交点.
①若∠A=50°,求∠D的度数;
②若∠A=,求∠E的度数(用含的代数式表示);
(2)如图Ⅱ,已知B、C分别是∠MAN的两边AM、AN上的动点,连结BC,∠MBC的平分线所在的直线与
∠ACB的平分线交于点P,试探究∠BPC与∠A的数量关系,并说明理由.
(满分150分,时间120分
)
A.基础闯关(90分)
一、选择题(每道题只有一个正确答案,每小题4分,共计28分)
1.已知某n边形的外角和恰好等于它的内角和的2倍,则n=(
)
A.
3??????
B.
4???????
C.
5????????
D.
6
2.如图,为了估计池塘岸边A,B两点间的距离,小彤同学在池塘一侧
选取一点O,测得OA=11米,OB=6米,则A,B间的距离可能是(?
)
3米??????
B.
4米??????C.
5米???????D.
6米
3.等腰三角形的一个底角为63?
,则它的顶角为(??
)
A.
60???????
B.
58??????
C.
56????????
D.
54?
4.在下列各图中,分别画出了△ABC中BC边上的高AD,其中正确的是(??
)
5.已知等腰△ABC的两边长分别为3cm和7cm,则△ABC的周长为(
)
A.
13cm?????
B.
17cm??????C.
13cm或17cm?????D.不能确定
6.以下几种多边形中,不能用于铺设无缝地板的是(
)
A.正三角形
B.正四边形
C.正五边形
D.正六边形
7.如图,一副三角板叠在一起如图所示放置,最小锐角
的点D恰好放在等腰直角三角板的斜边AB上,BC与DE
交于点M,如果∠ADF=96°,那么∠BME为(
).
A.101°???
B.
100°??
C.
99°???
D.
98°
二、填空题(每小题4分,共12分)
8.自行车的车身为三角形结构,这样做根据的数学道理是___________________;
9.用三种不同的正多边形地砖铺满地面,若其中有正方形,正六边形,则另一个为正
边形;
10.两个完全相同的正五边形都有一边在直线l上,且有一个公共顶点O,
其摆放方式如图所示,则∠AOB等于________度.
三、解答题(50分)
11.(8分)已知:某正多边形的一个外角是它相邻的内角的
,求这个多边形的边数.
12.(8分)等腰△ABC中,腰AB=AC,BD是AC边上的中线,已知△ABD的周长比△BCD的周长大7cm,且腰长是底边长的2倍,求△ABC的周长.
13.(8分)小华从点A出发向前走8米,向右转36?然后继续向前走8米,再向右转36?,他以同样的方法继续走下去,他能回到点A吗?若能,当他走回到点A时共走多少米?若不能,写出理由。
14.(8分)如果同时选用边长相等的正三角形和正方形(数量自定)密铺地板,可以怎样搭配?请画出两种密铺示意图。
15.(8分)一个零件的形状如图,按规定∠A=92?,∠C=26?,∠B=28?,检验已量得∠BDC=150?,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
16.(10分)如图,已知△ABC,求证:∠A+∠B+∠C=180?.
A
B
C
B.巩固新知(30分)
一、选择题(每道题只有一个正确答案,每小题4分,共计12分)
17.已知△ABC满足以下某个条件,一定能判定△ABC是直角三角形的是(
)
A.
∠A:∠B:∠C=3:5:8
B.
C.
∠A+∠B=2∠C
D.
∠A-∠B=3∠C
18.若一个多边形有20条对角线,则这个多边形有(??
)条边.
A.
5???????B.
6???????C.
7????????D.
8
19.如图,长方形ABCD的长为6cm,宽为4cm,E、F分别是BC和CD的中点,
DE、BF交于点G,则四边形ABGD的面积是(??
).
A.
15
B.
16
C.
17
D.
18
二、填空题(每小题4分,共8分)
20.当三角形中一个内角是另一个内角的2倍时,我们称此三角形为“梦想三角形”.如果一个“梦想三角形”有一个角为96°,那么这个“梦想三角形”的最小内角的度数为________;
21.如图,三角形纸片ABC中,∠A=68°,∠B=72°,将纸片的一角折叠,
使点C落在△ABC内,则∠1+∠2的度数为
度.
三、解答题(10分)
22.(10分)如图,△ABC中,CE平分∠ACB,CD⊥AB于D,DF⊥CE交CE于F,
若∠A=50?,∠B=80?,求∠CDF的度数;
求证:∠DCE=
.
C.能力提升(16分)
23.(4分)右图8×8的网格图中,△ABC的三个顶点均在网格
交点处,如果每个小方格的面积是1,那么:
△ABC的面积是________;
若边AB长5,则AB边上的高CD=______;
24.(12分)“转化”是数学中的一种重要思想。
(1)五角星图1的点A向下移动到BE的下方得到星形图2,请你根据学过的知识求出图2中∠A+∠B+∠C+∠D+∠E的度数;
(2)若对图2中星形截去∠A,如图3,请你求出∠B+∠C+∠D+∠E+∠F+∠G的度数;
(3)若再对图3中星形截去∠D,如图4,你能由题(2)中所得的方法或规律,猜想图4中的∠B+∠C+∠M+∠N+∠E+∠F+∠G的度数吗?(只要写出结论,不需要写出解题过程)
核心素养(14分)
25.(1)如图Ⅰ,在△ABC中,点D是两条内角平分线的交点,点E是两条外角平分线的交点.
①若∠A=50°,求∠D的度数;
②若∠A=,求∠E的度数(用含的代数式表示);
(2)如图Ⅱ,已知B、C分别是∠MAN的两边AM、AN上的动点,连结BC,∠MBC的平分线所在的直线与
∠ACB的平分线交于点P,试探究∠BPC与∠A的数量关系,并说明理由.
