粤教版 必修2 第03节 探究外力做功与物体动能变化的关系 :26张PPT
文档属性
| 名称 | 粤教版 必修2 第03节 探究外力做功与物体动能变化的关系 :26张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 521.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-06-10 20:35:04 | ||
图片预览








文档简介
(共26张PPT)
动能定理的应用
粤教版必修2
第四章第三节(第二课时)
学习目标
1、知道并理解动能定理,学会运用动能定理进行相关分析和计算。
2、通过一题多解,对比动能定理和动力学两种计算方法,体会动能定理解题的优越性。
动能定理公式
自学指导
应用动能定理解题的步骤
(1)确定研究对象和研究过程
(2)对研究对象进行受力分析
(3)写出研究过程中总功.
计算总功两种方法是什么?
W总=W1+W2+W3+......(功的代数和)
W总=F合Scosa(恒力做功)
(4)确定物体的初、末动能.
(5)按照动能定理列式求解.
例1:质量为m的物体在水平恒力F的
作用下,由静止开始前进s1后撤去力F,物体
与水平面的摩擦力恒为f,物体从开始到最终
停止运动的位移是多少?
(请尝试用动能定理和动力学两种方法解题。)
分组合作
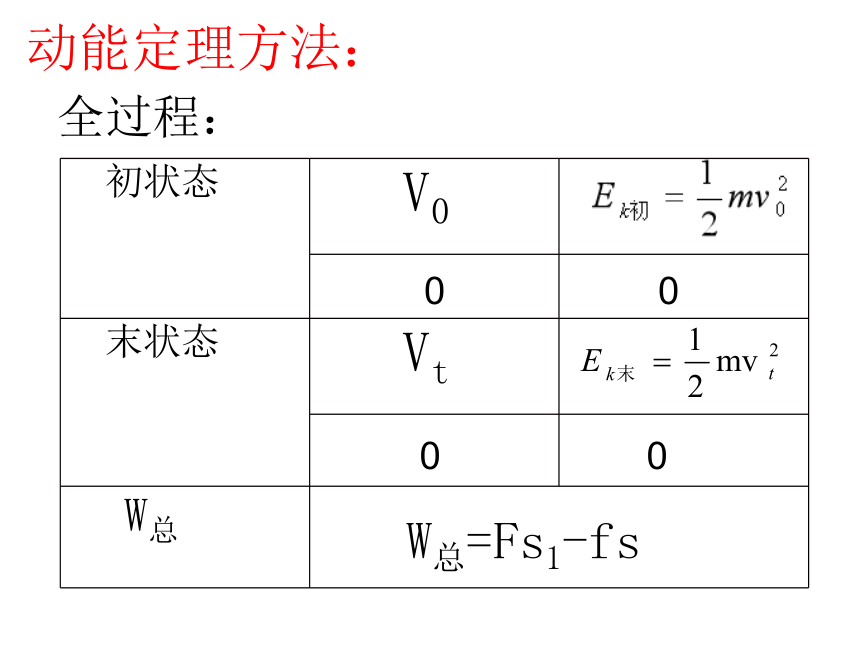
初状态
V0
末状态
Vt
W总
全过程:
W总=Fs1-fs
0
0
0
0
动能定理方法:
由动能定理得:
Fs1-fs=0-0
状态1
v0
状态2
v2
W12
状态3
v3
W23
分段法:
W12=Fs1-fs1
0
0
0
0
W23=-f(s-s1)
由动能定理得:
对于物体从状态1到状态2的过程:
从状态2到状态3的过程:
联立以上两式可得:
Fs1-fs=0
动力学方法:
由牛顿第二定律和匀变速直线运动公式得:
物体从状态1到状态2:v2-0=2a1s1
F-f=ma1
物体从状态2到状态3:0-v2=2a2(s-s1)
-f=ma2
联立以上式子解得
作业:如右图所示,一质量为2
kg的铅球从离地面2
m高处自由下落,陷入沙面水平的沙坑中的深度为2
cm,求沙子对铅球的平均阻力.(g取10
m/s2)
思路点拨:找出全过程初末状态的动能及重力、阻力做功、利用功能定理列式求解.
初状态
V0
末状态
Vt
W总
全过程:
W总=mg(H+h)-fh
0
0
0
0
动能定理方法
由动能定理得:
mg(H+h)-fh=0-0
f=2020N
状态1
v1
状态2
v2
W12
状态3
v3
W23
分段法:
W12=mgH
0
0
0
0
W23=mgh-fh
由动能定理得:
对于物体从状态1到状态2的过程:
从状态2到状态3的过程:
联立以上式子可得:
mg(H+h)-fh=0
f=2020N
动力学方法:
由牛顿第二定律和匀变速直线运动公式得:
物体从状态1到状态2:v2-0=2gH
物体从状态2到状态3:0-v2=2a2h
mg-f=ma2
联立以上式子解得:
f=2020N
课后练习
1、一个25
kg的小孩从高度为3.0
m的滑梯顶端由静止开始滑下,滑到底端时的速度为2.0
m/s.取g=10
m/s2,关于力对小孩做的功,以下结果正确的是( )
A.合外力做功50
J
B.阻力做功500
J
C.重力做功500
J
D.支持力做功50
J
解析:重力做功WG=mgh=25×10×3
J=750
J,C错;小孩所受支持力方向上的位移为零,故支持力做的功为零,D错;合外力做的功W合=Ek-0,即W合=
mv2=
×25×22
J=50
J,A正确;WG-W阻=Ek-0,做W阻=mgh-
mv2=750
J-50
J=700
J,B项错误.
答案:A
2.一人用力踢质量为1
kg的静止足球,使球以10
m/s的水平速度飞出,设人踢球的平均作用力为200
N,球在水平方向滚动的距离为20
m,则人对球做功为(g取10
m/s2)( )
A.50
J B.200
J
C.4
000
J
D.6
000
J
A
3.一质量为m的小球,用长为l的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点很缓慢地移动到Q点,如右图所示,则力F所做的功为( )
A.mglcos
θ
B.Flsin
θ
C.mgl(1-cos
θ)
D.Flcos
θ
解析:从P到Q小球缓慢移动可以认为小球的动能未变化,即ΔEk=0,设拉力F做的功为WF,则从P到Q,外力对球做的总功W=WF-mgl(1-cos
θ),由动能定理W=ΔEk得WF-mgl(1-cos
θ)=0,故WF=mgl(1-cos
θ),C正确.
答案:C
4.一辆汽车以v1=6
m/s的速度沿水平路面行驶时,急刹车后能滑行s1=3.6
m,如果以v2=8
m/s的速度行驶,在同样路面上急刹车后滑行的距离s2应为多少?
本小节结束
动能定理的应用
粤教版必修2
第四章第三节(第二课时)
学习目标
1、知道并理解动能定理,学会运用动能定理进行相关分析和计算。
2、通过一题多解,对比动能定理和动力学两种计算方法,体会动能定理解题的优越性。
动能定理公式
自学指导
应用动能定理解题的步骤
(1)确定研究对象和研究过程
(2)对研究对象进行受力分析
(3)写出研究过程中总功.
计算总功两种方法是什么?
W总=W1+W2+W3+......(功的代数和)
W总=F合Scosa(恒力做功)
(4)确定物体的初、末动能.
(5)按照动能定理列式求解.
例1:质量为m的物体在水平恒力F的
作用下,由静止开始前进s1后撤去力F,物体
与水平面的摩擦力恒为f,物体从开始到最终
停止运动的位移是多少?
(请尝试用动能定理和动力学两种方法解题。)
分组合作
初状态
V0
末状态
Vt
W总
全过程:
W总=Fs1-fs
0
0
0
0
动能定理方法:
由动能定理得:
Fs1-fs=0-0
状态1
v0
状态2
v2
W12
状态3
v3
W23
分段法:
W12=Fs1-fs1
0
0
0
0
W23=-f(s-s1)
由动能定理得:
对于物体从状态1到状态2的过程:
从状态2到状态3的过程:
联立以上两式可得:
Fs1-fs=0
动力学方法:
由牛顿第二定律和匀变速直线运动公式得:
物体从状态1到状态2:v2-0=2a1s1
F-f=ma1
物体从状态2到状态3:0-v2=2a2(s-s1)
-f=ma2
联立以上式子解得
作业:如右图所示,一质量为2
kg的铅球从离地面2
m高处自由下落,陷入沙面水平的沙坑中的深度为2
cm,求沙子对铅球的平均阻力.(g取10
m/s2)
思路点拨:找出全过程初末状态的动能及重力、阻力做功、利用功能定理列式求解.
初状态
V0
末状态
Vt
W总
全过程:
W总=mg(H+h)-fh
0
0
0
0
动能定理方法
由动能定理得:
mg(H+h)-fh=0-0
f=2020N
状态1
v1
状态2
v2
W12
状态3
v3
W23
分段法:
W12=mgH
0
0
0
0
W23=mgh-fh
由动能定理得:
对于物体从状态1到状态2的过程:
从状态2到状态3的过程:
联立以上式子可得:
mg(H+h)-fh=0
f=2020N
动力学方法:
由牛顿第二定律和匀变速直线运动公式得:
物体从状态1到状态2:v2-0=2gH
物体从状态2到状态3:0-v2=2a2h
mg-f=ma2
联立以上式子解得:
f=2020N
课后练习
1、一个25
kg的小孩从高度为3.0
m的滑梯顶端由静止开始滑下,滑到底端时的速度为2.0
m/s.取g=10
m/s2,关于力对小孩做的功,以下结果正确的是( )
A.合外力做功50
J
B.阻力做功500
J
C.重力做功500
J
D.支持力做功50
J
解析:重力做功WG=mgh=25×10×3
J=750
J,C错;小孩所受支持力方向上的位移为零,故支持力做的功为零,D错;合外力做的功W合=Ek-0,即W合=
mv2=
×25×22
J=50
J,A正确;WG-W阻=Ek-0,做W阻=mgh-
mv2=750
J-50
J=700
J,B项错误.
答案:A
2.一人用力踢质量为1
kg的静止足球,使球以10
m/s的水平速度飞出,设人踢球的平均作用力为200
N,球在水平方向滚动的距离为20
m,则人对球做功为(g取10
m/s2)( )
A.50
J B.200
J
C.4
000
J
D.6
000
J
A
3.一质量为m的小球,用长为l的轻绳悬挂于O点.小球在水平力F作用下,从平衡位置P点很缓慢地移动到Q点,如右图所示,则力F所做的功为( )
A.mglcos
θ
B.Flsin
θ
C.mgl(1-cos
θ)
D.Flcos
θ
解析:从P到Q小球缓慢移动可以认为小球的动能未变化,即ΔEk=0,设拉力F做的功为WF,则从P到Q,外力对球做的总功W=WF-mgl(1-cos
θ),由动能定理W=ΔEk得WF-mgl(1-cos
θ)=0,故WF=mgl(1-cos
θ),C正确.
答案:C
4.一辆汽车以v1=6
m/s的速度沿水平路面行驶时,急刹车后能滑行s1=3.6
m,如果以v2=8
m/s的速度行驶,在同样路面上急刹车后滑行的距离s2应为多少?
本小节结束
同课章节目录
- 第一章 抛体运动
- 第01节 什么是抛体运动
- 第02节 运动的合成与分解
- 第03节 竖直方向的抛体运动
- 第04节 平抛运动
- 第05节 斜抛运动
- 第二章 圆周运动
- 第01节 匀速圆周运动
- 第02节 向心力
- 第03节 离心现象及其应用
- 第三章 万有引力定律及其应用
- 第01节 万有引力定律
- 第02节 万有引力定律的应用
- 第03节 飞向太空
- 第四章 机械能和能源
- 第01节 功
- 第02节 动能 势能
- 第03节 探究外力做功与物体动能变化的关系
- 第04节 机械能守恒定律
- 第05节 验证机械能守恒定律
- 第06节 能量 能量转化与守恒定律
- 第07节 功率
- 第08节 能源的开发与利用
- 第五章 经典力学与物理学的革命
- 第01节 经典力学的成就与局限性
- 第02节 经典时空观与相对论时空观
- 第03节 量子化现象
- 第04节 物理学——人类文明进步的阶梯
