人教高中数学必修二1.1.2简单多面体的外接球问题(18张PPT)
文档属性
| 名称 | 人教高中数学必修二1.1.2简单多面体的外接球问题(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 12:32:34 | ||
图片预览


文档简介
(共19张PPT)
简单多面体的外接球问题
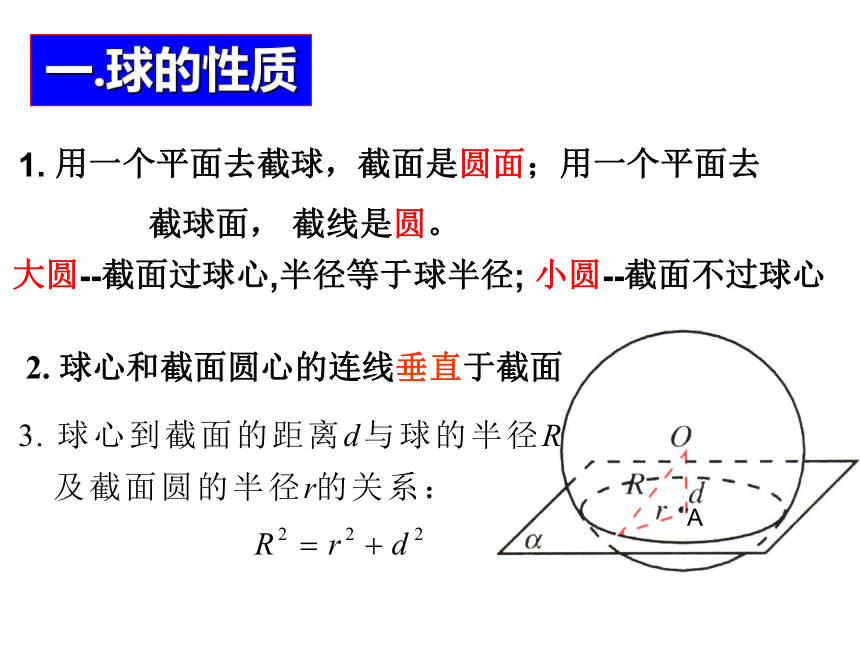
一.球的性质
1.
用一个平面去截球,截面是圆面;用一个平面去
截球面,
截线是圆。
大圆--截面过球心,半径等于球半径;
小圆--截面不过球心
2.
球心和截面圆心的连线垂直于截面
三.
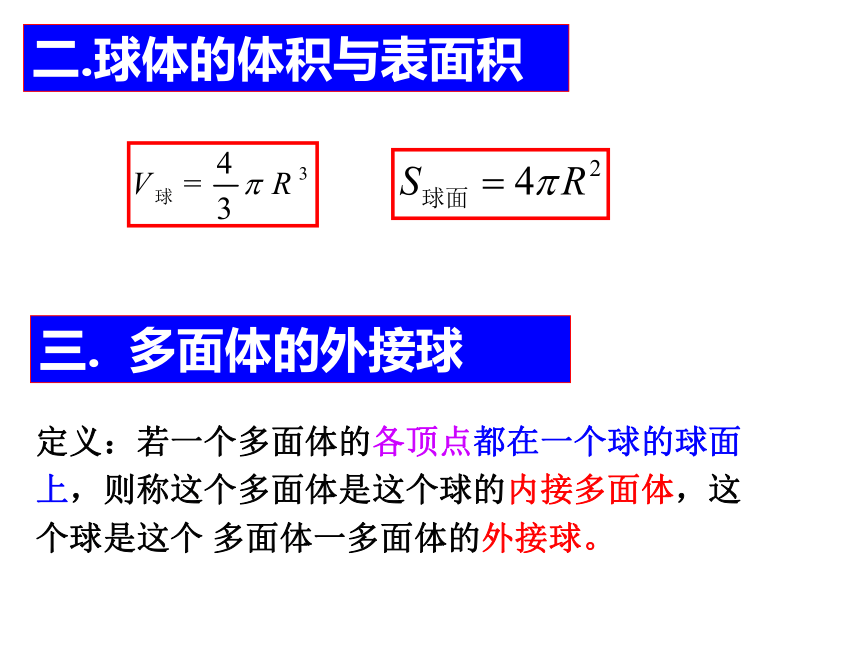
多面体的外接球
定义:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个
多面体一多面体的外接球。
二.球体的体积与表面积
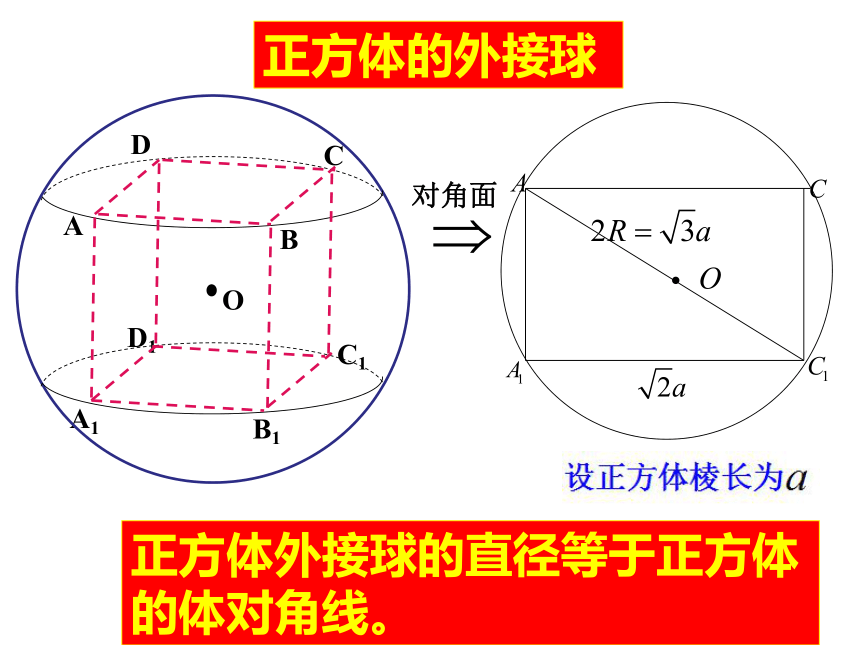
正方体外接球的直径等于正方体的体对角线。
正方体的外接球
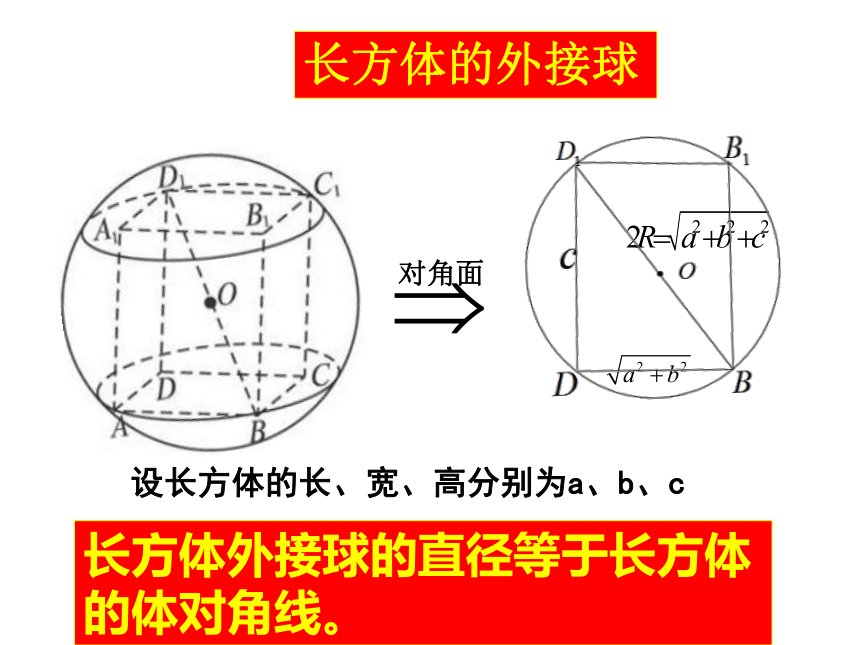
长方体的外接球
对角面
设长方体的长、宽、高分别为a、b、c
长方体外接球的直径等于长方体的体对角线。
两招搞定简单多面体外接球问题
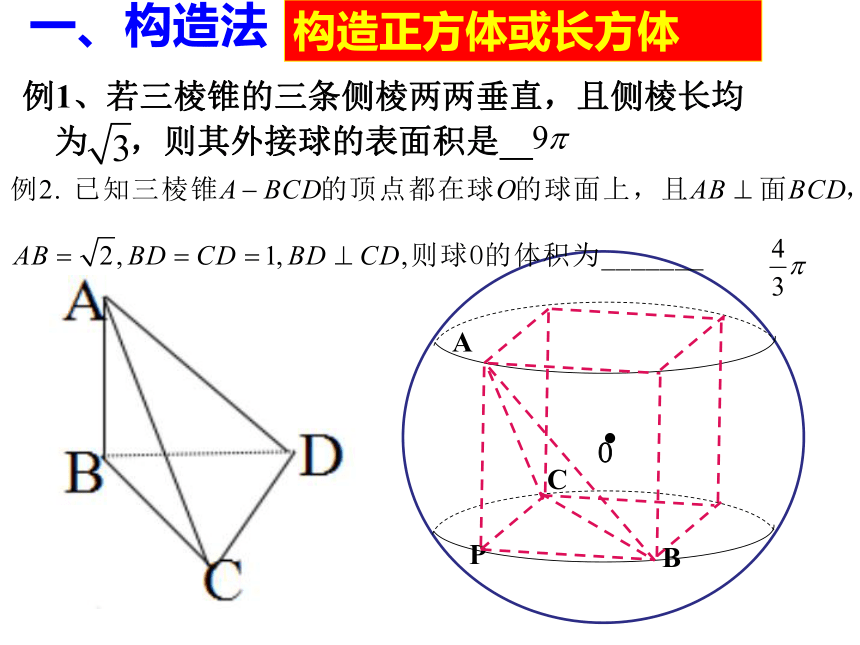
一、构造法
例1、若三棱锥的三条侧棱两两垂直,且侧棱长均为
,则其外接球的表面积是
构造正方体或长方体
例3.
求棱长为
a
的正四面体
D
–
ABC
的外接球的表面积。
思考总结:什么样的三棱锥可构造成正方体或长方体?
一、构造法
构造正方体或长方体
例1、若三棱锥的三条侧棱两两垂直,且侧棱长均为
,则其外接球的表面积是
三条侧棱两两垂直的三棱锥
一条侧棱垂直于底面,底面是直角三角形的三棱锥
例3、
求棱长为
a
的正四面体
D
–
ABC
的外接球的表面积。
正四面体
对棱相等的三棱锥
二、确定球心位置法
1.利用球的定义即球心到球面上各个点的距离都相等。
例5.
在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为
翻折前后的垂直关系和长度是否改变?
上下底面中心的连线的中点
在其高上
例7、求棱长为1的正四面体外接球的体积.
谈谈收获
1.
正方体,长方体,正棱柱,正棱锥的外接球球心位置
3.
求三棱锥的外接球两招:构造法;确定球心位置法
2.
棱长为a的正四面体外接球半径
感觉到数学的美,感觉到数与形的协调,感觉到几何的优雅,这是所有真正的数学家都清楚的真实的美的感觉。
—?—庞加莱
布置作业
给学生印发一张球的切接专题试卷!
简单多面体的外接球问题
一.球的性质
1.
用一个平面去截球,截面是圆面;用一个平面去
截球面,
截线是圆。
大圆--截面过球心,半径等于球半径;
小圆--截面不过球心
2.
球心和截面圆心的连线垂直于截面
三.
多面体的外接球
定义:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个
多面体一多面体的外接球。
二.球体的体积与表面积
正方体外接球的直径等于正方体的体对角线。
正方体的外接球
长方体的外接球
对角面
设长方体的长、宽、高分别为a、b、c
长方体外接球的直径等于长方体的体对角线。
两招搞定简单多面体外接球问题
一、构造法
例1、若三棱锥的三条侧棱两两垂直,且侧棱长均为
,则其外接球的表面积是
构造正方体或长方体
例3.
求棱长为
a
的正四面体
D
–
ABC
的外接球的表面积。
思考总结:什么样的三棱锥可构造成正方体或长方体?
一、构造法
构造正方体或长方体
例1、若三棱锥的三条侧棱两两垂直,且侧棱长均为
,则其外接球的表面积是
三条侧棱两两垂直的三棱锥
一条侧棱垂直于底面,底面是直角三角形的三棱锥
例3、
求棱长为
a
的正四面体
D
–
ABC
的外接球的表面积。
正四面体
对棱相等的三棱锥
二、确定球心位置法
1.利用球的定义即球心到球面上各个点的距离都相等。
例5.
在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为
翻折前后的垂直关系和长度是否改变?
上下底面中心的连线的中点
在其高上
例7、求棱长为1的正四面体外接球的体积.
谈谈收获
1.
正方体,长方体,正棱柱,正棱锥的外接球球心位置
3.
求三棱锥的外接球两招:构造法;确定球心位置法
2.
棱长为a的正四面体外接球半径
感觉到数学的美,感觉到数与形的协调,感觉到几何的优雅,这是所有真正的数学家都清楚的真实的美的感觉。
—?—庞加莱
布置作业
给学生印发一张球的切接专题试卷!
