平面向量的基本定理及坐标表示
图片预览







文档简介
(共45张PPT)
思考:给定平面内任意两个向量 、
,请你作向量 和 .
平面内的任意一向量是否都可以用
形如 的向量表示?
探究(一):平面向量基本定理
O
C
将三个向量的起点移到同一点:
O
A
C
将三个向量的起点移到同一点:
B
O
A
C
将三个向量的起点移到同一点:
B
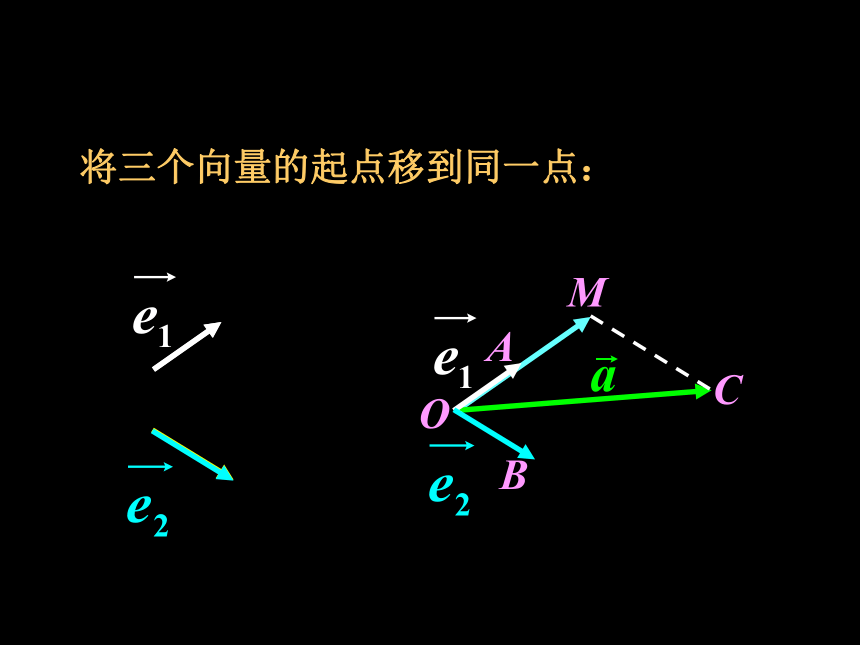
O
A
M
C
将三个向量的起点移到同一点:
B
N
O
A
M
C
将三个向量的起点移到同一点:
N
O
A
M
B
C
平面向量基本定理:
平面向量基本定理:
向量的一组基底.
平面向量基本定理:
B
O
O
A
B
C
A
C
B
O
O
A
B
C
A
C
B'
B'
O
A
M
B
C
B
O
A
C
B'
O
A
M
B
N
C
B
O
A
C
B
B'
O
O
A
M
B
N
C
A
C
A'
B
M
B'
O
O
A
M
B
N
C
A
C
A'
B
N
M
B'
O
O
A
M
B
N
C
A
C
A'
【例1】
【练1】如图,在平行四边形ABCD中,
=a, =b, E、M分别是AD、DC的中点,点F在BC上,且BC=3BF,以a,b为基底分别表示向量 和 .
A
B
E
D
C
F
M
探究(二):平面向量的正交分解及坐标表示
1. 向量的夹角
探究(二):平面向量的正交分解及坐标表示
1. 向量的夹角
O
B
A
探究(二):平面向量的正交分解及坐标表示
1. 向量的夹角
O
B
A
1. 向量的夹角
探究(二):平面向量的正交分解及坐标表示
O
B
A
注:
O
B
A
O
B
A
注:
O
B
A
【练2】
在正三角形ABC中, 与 、 的夹角分别等于________
A
B
C
B
A
O
【例3】
思考 :如果向量a与b的夹角是90°,则称向量a与b垂直,记作a⊥b. 互相垂直的两个向量能否作为平面内所有向量的一组基底?
b
a
把一个向量分解为两个互相垂直的向量,叫做把向量正交分解. 如图,向量i、j是两个互相垂直的单位向量,向量a与i的夹角是30°,且|a|=4,以向量i、j为基底,向量a如何表示?
B
a
i
O
j
A
P
2. 向量的正交分解及坐标表示
把一个向量分解为两个互相垂直的向量,叫做把向量正交分解. 如图,向量i、j是两个互相垂直的单位向量,向量a与i的夹角是30°,且|a|=4,以向量i、j为基底,向量a如何表示?
B
a
i
O
j
A
P
2. 向量的正交分解及坐标表示
在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i、j作为基底,对于平面内的一个向量a,由平面向量基本定理知,有且只有一对实数x、y,使得 a=xi+yj.我们把有序数对(x,y)叫做向量a的坐标,记作a=(x,y).其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标,上式叫
做向量的坐标表示.
那么x、y的几何意义如何?
a
i
x
y
O
j
x
y
相等向量的坐标必然相等,作向量 a, 则 (x,y),此时点A是坐标是什么?
A
a
i
x
y
O
j
A(x, y)
如图,OM//AB,点P在由射线OM、线段OB及AB的延长线围成的阴影区域内(不含边界),且 (1) 则x的取值范围是________ (2) 当 时, y的取值范围 是______
思考题
O
B
A
M
P
1. 平面向量基本定理是建立在向量加法和数乘运算基础上的向量分解原理,同时又是向量坐标表示的理论依据, 是一个承前起后的重要知识点.
2. 向量的夹角是反映两个向量相对位置关系的一个几何量,平行向量的夹角是0°或180°,垂直向量的夹角是90°.
课堂小结
3. 向量的坐标表示是一种向量与坐标的对应关系,它使得向量具有代数意义.将向量的起点平移到坐标原点,则平移后向量的终点坐标就是向量的坐标.
考一本 第18课时
作业布置
思考:给定平面内任意两个向量 、
,请你作向量 和 .
平面内的任意一向量是否都可以用
形如 的向量表示?
探究(一):平面向量基本定理
O
C
将三个向量的起点移到同一点:
O
A
C
将三个向量的起点移到同一点:
B
O
A
C
将三个向量的起点移到同一点:
B
O
A
M
C
将三个向量的起点移到同一点:
B
N
O
A
M
C
将三个向量的起点移到同一点:
N
O
A
M
B
C
平面向量基本定理:
平面向量基本定理:
向量的一组基底.
平面向量基本定理:
B
O
O
A
B
C
A
C
B
O
O
A
B
C
A
C
B'
B'
O
A
M
B
C
B
O
A
C
B'
O
A
M
B
N
C
B
O
A
C
B
B'
O
O
A
M
B
N
C
A
C
A'
B
M
B'
O
O
A
M
B
N
C
A
C
A'
B
N
M
B'
O
O
A
M
B
N
C
A
C
A'
【例1】
【练1】如图,在平行四边形ABCD中,
=a, =b, E、M分别是AD、DC的中点,点F在BC上,且BC=3BF,以a,b为基底分别表示向量 和 .
A
B
E
D
C
F
M
探究(二):平面向量的正交分解及坐标表示
1. 向量的夹角
探究(二):平面向量的正交分解及坐标表示
1. 向量的夹角
O
B
A
探究(二):平面向量的正交分解及坐标表示
1. 向量的夹角
O
B
A
1. 向量的夹角
探究(二):平面向量的正交分解及坐标表示
O
B
A
注:
O
B
A
O
B
A
注:
O
B
A
【练2】
在正三角形ABC中, 与 、 的夹角分别等于________
A
B
C
B
A
O
【例3】
思考 :如果向量a与b的夹角是90°,则称向量a与b垂直,记作a⊥b. 互相垂直的两个向量能否作为平面内所有向量的一组基底?
b
a
把一个向量分解为两个互相垂直的向量,叫做把向量正交分解. 如图,向量i、j是两个互相垂直的单位向量,向量a与i的夹角是30°,且|a|=4,以向量i、j为基底,向量a如何表示?
B
a
i
O
j
A
P
2. 向量的正交分解及坐标表示
把一个向量分解为两个互相垂直的向量,叫做把向量正交分解. 如图,向量i、j是两个互相垂直的单位向量,向量a与i的夹角是30°,且|a|=4,以向量i、j为基底,向量a如何表示?
B
a
i
O
j
A
P
2. 向量的正交分解及坐标表示
在平面直角坐标系中,分别取与x轴、y轴方向相同的两个单位向量i、j作为基底,对于平面内的一个向量a,由平面向量基本定理知,有且只有一对实数x、y,使得 a=xi+yj.我们把有序数对(x,y)叫做向量a的坐标,记作a=(x,y).其中x叫做a在x轴上的坐标,y叫做a在y轴上的坐标,上式叫
做向量的坐标表示.
那么x、y的几何意义如何?
a
i
x
y
O
j
x
y
相等向量的坐标必然相等,作向量 a, 则 (x,y),此时点A是坐标是什么?
A
a
i
x
y
O
j
A(x, y)
如图,OM//AB,点P在由射线OM、线段OB及AB的延长线围成的阴影区域内(不含边界),且 (1) 则x的取值范围是________ (2) 当 时, y的取值范围 是______
思考题
O
B
A
M
P
1. 平面向量基本定理是建立在向量加法和数乘运算基础上的向量分解原理,同时又是向量坐标表示的理论依据, 是一个承前起后的重要知识点.
2. 向量的夹角是反映两个向量相对位置关系的一个几何量,平行向量的夹角是0°或180°,垂直向量的夹角是90°.
课堂小结
3. 向量的坐标表示是一种向量与坐标的对应关系,它使得向量具有代数意义.将向量的起点平移到坐标原点,则平移后向量的终点坐标就是向量的坐标.
考一本 第18课时
作业布置
