北师大版数学七年级下册3.3 用图象表示的变量间关系同步练习(含答案)
文档属性
| 名称 | 北师大版数学七年级下册3.3 用图象表示的变量间关系同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 573.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 11:19:44 | ||
图片预览



文档简介
第三章
变量之间的关系
3.3
用图象表示的变量间关系
1.
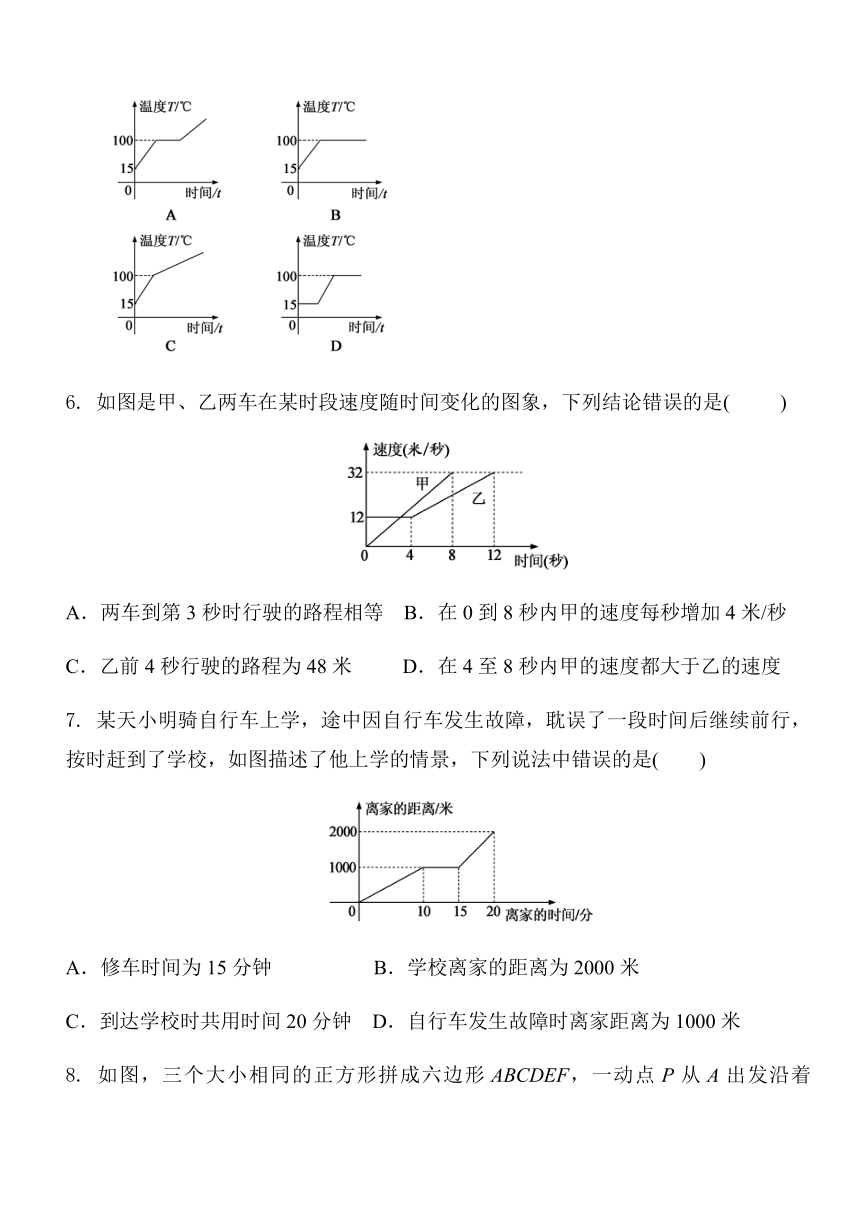
星期天张老师从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映这段时间张老师离家的距离y(米)与时间x(分钟)之间关系的大致图象是(
)
2.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同,如图所示,反映了一天24小时小明的体温变化情况,下列说法中,错误的是(
)
A.清晨5时,体温最低
B.下午5时,体温最高
C.这一天中小明体温T(℃)的范围是36.5≤T≤37.5
D.从5时至24时,小明的体温一直是升高的
3.
某公司的生产量在七个月之内的增长变化情况如图所示,下列结论错误的是(
)
A.2月-6月生产量增长率逐月减少
B.7月份生产量的增长率开始回升
C.这七个月中,生产量有上涨有下跌
D.这七个月中,每月生产量不断上涨
4.
如图是我市某一天内的气温变化图,根据图象,下列说法中错误的是(
)
A.这一天中最高气温约是37℃
B.这一天中最高气温与最低气温的差约为15℃
C.这一天中3时至15时之间的气温在逐渐升高
D.这一天中只有15时至24时之间的气温在逐渐降低
5.
在一个标准大气压下,能反映水在均匀加热过程中,水的温度(T)随加热时间(t)变化的图象大致是(
)
6.
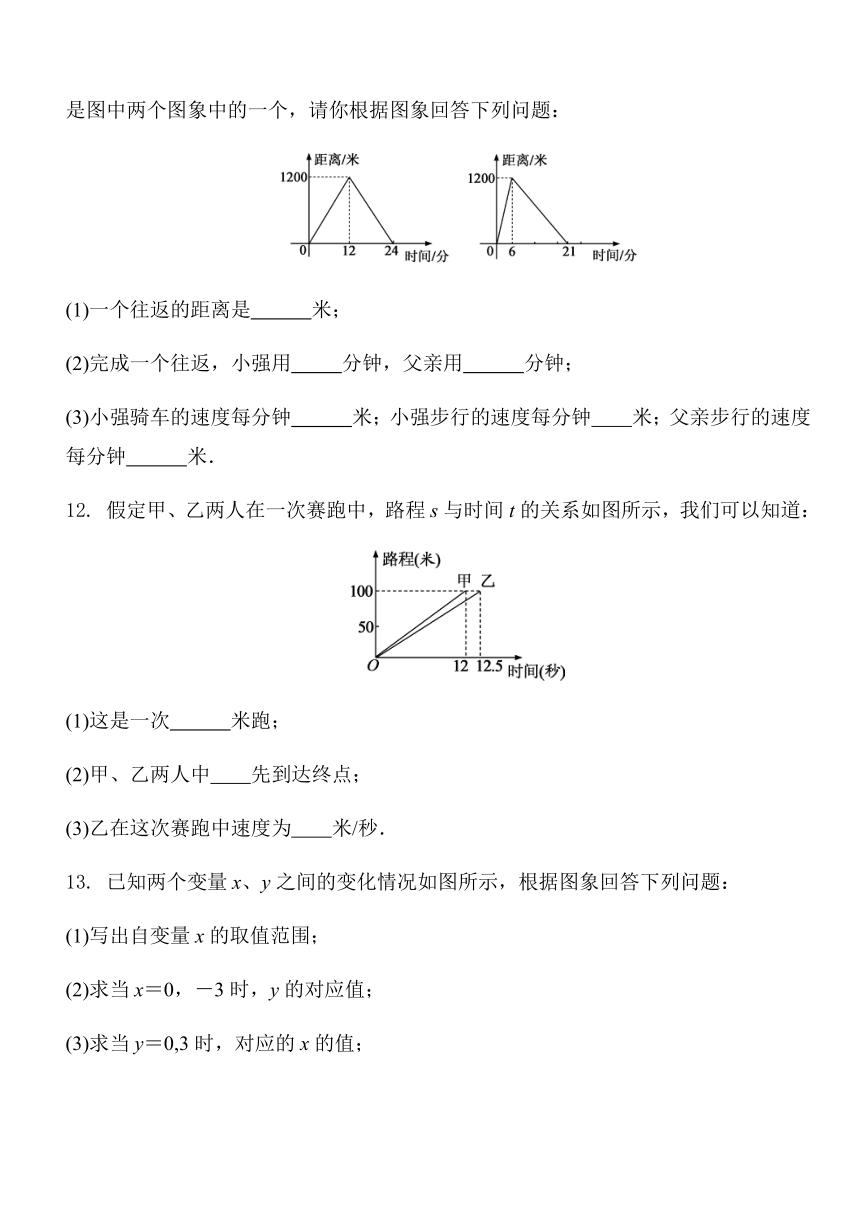
如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是(
)
A.两车到第3秒时行驶的路程相等
B.在0到8秒内甲的速度每秒增加4米/秒
C.乙前4秒行驶的路程为48米
D.在4至8秒内甲的速度都大于乙的速度
7.
某天小明骑自行车上学,途中因自行车发生故障,耽误了一段时间后继续前行,按时赶到了学校,如图描述了他上学的情景,下列说法中错误的是(
)
A.修车时间为15分钟
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.自行车发生故障时离家距离为1000米
8.
如图,三个大小相同的正方形拼成六边形ABCDEF,一动点P从A出发沿着A—B—C—D—E匀速运动,最后到达E,运动过程中三角形PEF的面积(S)随时间(t)变化的图象大致是(
)
9.
小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是(
)
0.
以“春城”而享誉中外的昆明大多数地区夏无酷暑,冬无严寒.如图,是昆明冬季某一天的气温随时间变化的图象.请根据图象回答,在 时气温最低,最低气温是 ℃,当天最高气温为 ℃,这一天的温差为 ℃;从最低气温到最高气温经过了 小时,从 到 时温度上升,图中A点表示
.
11.
小强与父亲同时出发,到达同一目的地都立即返回,小强去时骑自行车,返回时步行;父亲往返都是步行,两人的步行速度不等,每个人的往返路程与时间关系分别是图中两个图象中的一个,请你根据图象回答下列问题:
(1)一个往返的距离是
米;
(2)完成一个往返,小强用
分钟,父亲用
分钟;
(3)小强骑车的速度每分钟
米;小强步行的速度每分钟 米;父亲步行的速度每分钟
米.
12.
假定甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,我们可以知道:
(1)这是一次
米跑;
(2)甲、乙两人中 先到达终点;
(3)乙在这次赛跑中速度为 米/秒.
13.
已知两个变量x、y之间的变化情况如图所示,根据图象回答下列问题:
(1)写出自变量x的取值范围;
(2)求当x=0,-3时,y的对应值;
(3)求当y=0,3时,对应的x的值;
(4)当x为何值时,y的值最大?
(5)当x在什么范围内时,y的值在不断增加?
14.
小明在同样的两个容器中盛满水,加热到相同温度,然后用厚度相同的1、2两种保温材料包好,每隔5分钟测量一次两个容器中水的温度.实验过程中室温保持不变,最后他把记录的温度画成了如图所示的图象,其中横轴表示时间,纵轴表示温度.仔细观察图象,然后回答问题.
(1)小明把水加热到了多少度,后来降到了多少度?
(2)半小时后,哪个容器中水的温度稍高些,你是怎样看出来的?
(3)你估计当时室温可能是多少度?说一说你估计的依据;
(4)你认为哪种保温材料保温性能更好些?说说你的理由.
15.
星期天小明骑自行车去新华书店,最初以某一速度匀速行驶,中途由于某事耽误了几分钟,为了节约时间,他加快了速度,仍保持匀速行驶,终于按原计划到了新华书店.晚上回到家,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)小明家距离新华书店多远?小明总共用了多长时间到达新华书店?
(3)出发后0.2小时到0.3小时之间可能发生了什么情况?
16.
看图说故事.
请你编写一个故事,使故事情境中出现的一对变量x、y满足图示的函数关系,要求:
(1)指出变量x和y的含义;
(2)利用图中的数据说明这对变量变化过程的实际意义,其中须涉及“速度”这个量.
17.
某气象站观察一场沙尘暴从发生到结束的全过程,开始时风速按一定的速度匀速增大,经过荒漠地时,风速增大得比较快,一段时间后,风速保持不变,当沙尘经过防风林时,其风速开始逐渐减小,最终停止.如图所示是风速与时间之间的关系的图象,结合图象回答下列问题:
(1)沙尘暴从开始发生到结束共经历了多长时间?
(2)从图象上看,风速在哪个时间段增大得比较快,增加的速度是多少?
(3)风速在哪个时间段保持不变,经历了多少时间?
(4)风速从开始减小到最终停止,风速每小时减小多少?
答案:
1---9
BDCDB
AABB
10.
4
0
12
12
10
4
14
20时的温度为10℃
11.
(1)
2400
(2)
21
24
(3)
200
80
100
12.
(1)
100
(2)
甲
(3)
8
13.
解:(1)-3≤x≤3.5;
(2)当x=0时,y=3,当x=-3时,y=1;
(3)当y=0时,x1=-2.5,x2=-1.5,x3=3.5,当y=3时,x1=0,x2=2;
(4)当x=1时,y最大=4;
(5)-2<x<1.
14.
解:(1)加热到80℃,后来又降到20℃;
(2)第1种材料的容器中水的温度稍高些.因为时间为30min时,第一种材料的容器的水温为54℃,第二种材料中的水温为38℃;
(3)约20℃,因为两容器的水温最后都降到这一温度后不再降低了;
(4)第1种保温材料的性能更好些,因为它包的容器降温速度相对比较慢.
15.
解:(1)行驶路程与行驶时间;
(2)4千米,0.4小时;
(3)比如自行车发生故障,遇见熟人说话等.
16.
解:(1)该函数图象表示小明骑车离出发地的路程ykm与他所用的时间x分的关系;
(2)小明以0.4km/min的速度匀速骑5min,在原地休息了6min,然后以0.5km/min的速度匀速骑车回出发地.
16.
解:(1)41.2小时;
(2)风速在5时~12时这个时间增大比较快,每小时增加4千米/时;
(3)风速在12时~26时这个时间段保持不变,经历14小时;
(4)风速每小时减小2.5千米/时.
变量之间的关系
3.3
用图象表示的变量间关系
1.
星期天张老师从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映这段时间张老师离家的距离y(米)与时间x(分钟)之间关系的大致图象是(
)
2.正常人的体温一般在37℃左右,但一天中的不同时刻不尽相同,如图所示,反映了一天24小时小明的体温变化情况,下列说法中,错误的是(
)
A.清晨5时,体温最低
B.下午5时,体温最高
C.这一天中小明体温T(℃)的范围是36.5≤T≤37.5
D.从5时至24时,小明的体温一直是升高的
3.
某公司的生产量在七个月之内的增长变化情况如图所示,下列结论错误的是(
)
A.2月-6月生产量增长率逐月减少
B.7月份生产量的增长率开始回升
C.这七个月中,生产量有上涨有下跌
D.这七个月中,每月生产量不断上涨
4.
如图是我市某一天内的气温变化图,根据图象,下列说法中错误的是(
)
A.这一天中最高气温约是37℃
B.这一天中最高气温与最低气温的差约为15℃
C.这一天中3时至15时之间的气温在逐渐升高
D.这一天中只有15时至24时之间的气温在逐渐降低
5.
在一个标准大气压下,能反映水在均匀加热过程中,水的温度(T)随加热时间(t)变化的图象大致是(
)
6.
如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是(
)
A.两车到第3秒时行驶的路程相等
B.在0到8秒内甲的速度每秒增加4米/秒
C.乙前4秒行驶的路程为48米
D.在4至8秒内甲的速度都大于乙的速度
7.
某天小明骑自行车上学,途中因自行车发生故障,耽误了一段时间后继续前行,按时赶到了学校,如图描述了他上学的情景,下列说法中错误的是(
)
A.修车时间为15分钟
B.学校离家的距离为2000米
C.到达学校时共用时间20分钟
D.自行车发生故障时离家距离为1000米
8.
如图,三个大小相同的正方形拼成六边形ABCDEF,一动点P从A出发沿着A—B—C—D—E匀速运动,最后到达E,运动过程中三角形PEF的面积(S)随时间(t)变化的图象大致是(
)
9.
小明的父亲从家走了20分钟到一个离家900米的书店,在书店看了10分钟书后,用15分钟返回家,下列图中表示小明的父亲离家的距离与时间的函数图象是(
)
0.
以“春城”而享誉中外的昆明大多数地区夏无酷暑,冬无严寒.如图,是昆明冬季某一天的气温随时间变化的图象.请根据图象回答,在 时气温最低,最低气温是 ℃,当天最高气温为 ℃,这一天的温差为 ℃;从最低气温到最高气温经过了 小时,从 到 时温度上升,图中A点表示
.
11.
小强与父亲同时出发,到达同一目的地都立即返回,小强去时骑自行车,返回时步行;父亲往返都是步行,两人的步行速度不等,每个人的往返路程与时间关系分别是图中两个图象中的一个,请你根据图象回答下列问题:
(1)一个往返的距离是
米;
(2)完成一个往返,小强用
分钟,父亲用
分钟;
(3)小强骑车的速度每分钟
米;小强步行的速度每分钟 米;父亲步行的速度每分钟
米.
12.
假定甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示,我们可以知道:
(1)这是一次
米跑;
(2)甲、乙两人中 先到达终点;
(3)乙在这次赛跑中速度为 米/秒.
13.
已知两个变量x、y之间的变化情况如图所示,根据图象回答下列问题:
(1)写出自变量x的取值范围;
(2)求当x=0,-3时,y的对应值;
(3)求当y=0,3时,对应的x的值;
(4)当x为何值时,y的值最大?
(5)当x在什么范围内时,y的值在不断增加?
14.
小明在同样的两个容器中盛满水,加热到相同温度,然后用厚度相同的1、2两种保温材料包好,每隔5分钟测量一次两个容器中水的温度.实验过程中室温保持不变,最后他把记录的温度画成了如图所示的图象,其中横轴表示时间,纵轴表示温度.仔细观察图象,然后回答问题.
(1)小明把水加热到了多少度,后来降到了多少度?
(2)半小时后,哪个容器中水的温度稍高些,你是怎样看出来的?
(3)你估计当时室温可能是多少度?说一说你估计的依据;
(4)你认为哪种保温材料保温性能更好些?说说你的理由.
15.
星期天小明骑自行车去新华书店,最初以某一速度匀速行驶,中途由于某事耽误了几分钟,为了节约时间,他加快了速度,仍保持匀速行驶,终于按原计划到了新华书店.晚上回到家,小明画了自行车行进路程s(km)与行进时间t(h)的图象,如图所示,请回答:
(1)这个图象反映了哪两个变量之间的关系?
(2)小明家距离新华书店多远?小明总共用了多长时间到达新华书店?
(3)出发后0.2小时到0.3小时之间可能发生了什么情况?
16.
看图说故事.
请你编写一个故事,使故事情境中出现的一对变量x、y满足图示的函数关系,要求:
(1)指出变量x和y的含义;
(2)利用图中的数据说明这对变量变化过程的实际意义,其中须涉及“速度”这个量.
17.
某气象站观察一场沙尘暴从发生到结束的全过程,开始时风速按一定的速度匀速增大,经过荒漠地时,风速增大得比较快,一段时间后,风速保持不变,当沙尘经过防风林时,其风速开始逐渐减小,最终停止.如图所示是风速与时间之间的关系的图象,结合图象回答下列问题:
(1)沙尘暴从开始发生到结束共经历了多长时间?
(2)从图象上看,风速在哪个时间段增大得比较快,增加的速度是多少?
(3)风速在哪个时间段保持不变,经历了多少时间?
(4)风速从开始减小到最终停止,风速每小时减小多少?
答案:
1---9
BDCDB
AABB
10.
4
0
12
12
10
4
14
20时的温度为10℃
11.
(1)
2400
(2)
21
24
(3)
200
80
100
12.
(1)
100
(2)
甲
(3)
8
13.
解:(1)-3≤x≤3.5;
(2)当x=0时,y=3,当x=-3时,y=1;
(3)当y=0时,x1=-2.5,x2=-1.5,x3=3.5,当y=3时,x1=0,x2=2;
(4)当x=1时,y最大=4;
(5)-2<x<1.
14.
解:(1)加热到80℃,后来又降到20℃;
(2)第1种材料的容器中水的温度稍高些.因为时间为30min时,第一种材料的容器的水温为54℃,第二种材料中的水温为38℃;
(3)约20℃,因为两容器的水温最后都降到这一温度后不再降低了;
(4)第1种保温材料的性能更好些,因为它包的容器降温速度相对比较慢.
15.
解:(1)行驶路程与行驶时间;
(2)4千米,0.4小时;
(3)比如自行车发生故障,遇见熟人说话等.
16.
解:(1)该函数图象表示小明骑车离出发地的路程ykm与他所用的时间x分的关系;
(2)小明以0.4km/min的速度匀速骑5min,在原地休息了6min,然后以0.5km/min的速度匀速骑车回出发地.
16.
解:(1)41.2小时;
(2)风速在5时~12时这个时间增大比较快,每小时增加4千米/时;
(3)风速在12时~26时这个时间段保持不变,经历14小时;
(4)风速每小时减小2.5千米/时.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
