湘教版七年级数学下册6.2方差课件(共24张PPT)
文档属性
| 名称 | 湘教版七年级数学下册6.2方差课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
6.2
方差
湘教版
七年级下册
学习目标
1.理解方差的概念及统计学意义;
2.会计算一组数据的方差;
(重点)
3.能够运用方差判断数据的波动程度,并解决简单的实际问题.(难点)
我们学习了数据分析的一些知识.平均数、中位数、众数是三个不同的代表数,可描述数据的数值的一般水平或集中趋势.
数据的分析要选择恰当的形式,要根据具体情况选用统计表、统计图,或者用平均数、众数、中位数来描述.
在数据分析中还有其他情况出现:
如:数据与其平均数的偏离程度。
如何分析数据的稳定性?
知识回顾
动脑筋
刘亮和李飞参加射击训练的成绩(单位:环)如下:
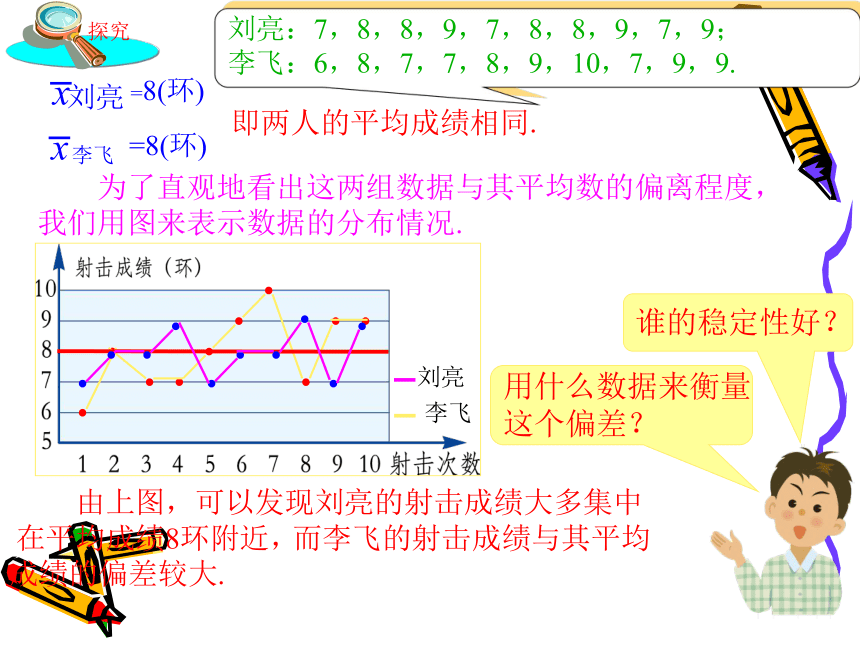
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
?
教练的烦恼
甲,乙两名射击手现要挑选一名射击手参加比赛.
若你是教练,你认为挑选哪一位比较适宜?
进入新课
(1)
两人的平均成绩分别是多少?
(2)
如何反映这两组数据与其平均数
的偏离程度?
(3)
谁的成绩比较稳定?
从哪几个问题考虑?
刘亮
李飞
即两人的平均成绩相同.
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
x
刘亮
=8(环)
x
李飞
=8(环)
探究
谁的稳定性好?
为了直观地看出这两组数据与其平均数的偏离程度,我们用图来表示数据的分布情况.
由上图,可以发现刘亮的射击成绩大多集中在平均成绩8环附近,
而李飞的射击成绩与其平均成绩的偏差较大.
用什么数据来衡量
这个偏差?
分别计算出两人射击成绩与平均成绩的偏差的和:
动脑筋
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
刘亮:(8-7)+(8-8)+…+(8-9)=0;
还是没区别,
怎么办?
分别计算出两人射击成绩与平均成绩的偏差的平方和:
刘亮:(8-7)2+(8-8)2+…+(8-9)2=6
李飞:(8-6)+(8-8)+…+(8-9)=0
李飞:(8-6)2+(8-8)2+…+(8-9)2=14
找到啦!
有区别了。
我们不如还把偏差的平方和缩小,即:
求偏差的平方和的平均数:
刘亮:[(8-7)2+(8-8)2+…+(8-9)2]÷10=0.6
李飞:[(8-6)2+(8-8)2+…+(8-9)2]÷10=1.4
刘亮的成绩与平均数的偏差比李飞的成绩与
平均数的偏差小,说明刘亮的成绩比较稳定。
一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征,它反映了一组数据的离散程度或波动大小.
那么如何用一个特征值来反映一组数据与其平均数的离散程度呢?
设一组数据为x1,x2,…,xn,各数据与平均数
之差的平方的平均值,叫做这组数据的方差,记做
s2.
即
由此我们可以算出刘亮、李飞的射击成绩的方差分别是
s2刘亮=0.6
s2李飞=1.4
计算结果表明:
s2李飞>
s2刘亮,这说明李飞的射击成绩波动大,而刘亮的射击成绩波动小,因此刘亮的射击成绩稳定.
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
有两个女声合唱队,各由5名队员组成,她们的身高为(单位:厘米):
甲队:160,162,159,160,159,
乙队:180,160,150,150,160.
如果单从队员的身高考虑,哪队的演出效果好?
解:
(1)甲队队员的平均身高是
乙队的平均身高是
甲队队员身高的方差是:
乙队队员身高的方差是:
不难算出每个队的平均身高都是160厘米,但甲队身高波动小,乙队身高波动大,单从身高考虑,甲队比较整齐,演出的效果会好一些.
方差反映的是一组数据哪个方面的特征?
方差反映的是一组数据与其平均数的偏离程度,方差越小,数据越集中;方差越大,数据越分散.
甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
某同学分析上表后得出如下结论:①甲、乙两班学生成绩平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论正确的有
.
班级
参加人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
①②③
做一做
①数据x1-3,x2-3,x3-3,…,xn-3
平均数为
,方差为
.
②数据x1+3,x2+3,x3+3,…,xn+3
平均数为
,方差为
.
若数据x1、x2、…、xn平均数为
,方差为s2,则
x
+3
x
-3
x
s2
s2
知识拓展
③数据3x1
,3x2
,3x3
,…,3xn
平均数为
,方差为
.
④数据2x1-3,2x2-3,2x3-3
,…,2xn-3
平均数为
,方差为
.
-3
2x
9s2
4s2
3x
(1)数据x1±b、x2±b、…、xn±b
平均数为
,
方差为
s2
+b
x
(2)数据ax1、ax2、…、axn
平均数为
,
方差为
a2s2
ax
1.样本方差的作用是(
)
A.表示总体的平均水平
B.表示样本的平均水平
C.准确表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
D
当堂练习
2.人数相同的八年级(1)、(2)两班学生在同一次数学单元测试中,班级平均分和方差下:
,
,
,则成绩较为稳定的班级是(
)
A.甲班
B.乙班
C.两班成绩一样稳定
D.无法确定
B
3.小凯同学参加数学竞赛训练,近期的五次测试成绩得分情况如图所示,则他这五次成绩的方差
为
.
100
4.在样本方差的计算公式
中,
数字10
表示___________
,数字20表示
_______.
样本容量
平均数
5.五个数1,3,a,5,8的平均数是4,则a
=_____,这五个数的方差_____.
3
5.6
6.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩
76
84
90
84
81
87
88
81
85
84
乙的成绩
82
86
87
90
79
81
93
90
74
78
(1)填写下表:
同学
平均成绩
中位数
众数
方差
85分以上的频率
甲
84
84
0.3
乙
84
84
34
84
90
0.5
14.4
(2)利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价.
解:从众数看,甲成绩的众数为84分,乙成绩的众数是90分,乙的成绩比甲好;
从方差看,s2甲=14.4,
s2乙=34,甲的成绩比乙相对稳定;从甲、乙的中位数、平均数看,中位数、平均数都是84分,两人成绩一样好;
从频率看,甲85分以上的次数比乙少,乙的成绩比甲好.
课堂小结
方差
方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).
公式:
谢谢,请提出宝贵意见!
6.2
方差
湘教版
七年级下册
学习目标
1.理解方差的概念及统计学意义;
2.会计算一组数据的方差;
(重点)
3.能够运用方差判断数据的波动程度,并解决简单的实际问题.(难点)
我们学习了数据分析的一些知识.平均数、中位数、众数是三个不同的代表数,可描述数据的数值的一般水平或集中趋势.
数据的分析要选择恰当的形式,要根据具体情况选用统计表、统计图,或者用平均数、众数、中位数来描述.
在数据分析中还有其他情况出现:
如:数据与其平均数的偏离程度。
如何分析数据的稳定性?
知识回顾
动脑筋
刘亮和李飞参加射击训练的成绩(单位:环)如下:
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
?
教练的烦恼
甲,乙两名射击手现要挑选一名射击手参加比赛.
若你是教练,你认为挑选哪一位比较适宜?
进入新课
(1)
两人的平均成绩分别是多少?
(2)
如何反映这两组数据与其平均数
的偏离程度?
(3)
谁的成绩比较稳定?
从哪几个问题考虑?
刘亮
李飞
即两人的平均成绩相同.
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
x
刘亮
=8(环)
x
李飞
=8(环)
探究
谁的稳定性好?
为了直观地看出这两组数据与其平均数的偏离程度,我们用图来表示数据的分布情况.
由上图,可以发现刘亮的射击成绩大多集中在平均成绩8环附近,
而李飞的射击成绩与其平均成绩的偏差较大.
用什么数据来衡量
这个偏差?
分别计算出两人射击成绩与平均成绩的偏差的和:
动脑筋
刘亮:7,8,8,9,7,8,8,9,7,9;
李飞:6,8,7,7,8,9,10,7,9,9.
刘亮:(8-7)+(8-8)+…+(8-9)=0;
还是没区别,
怎么办?
分别计算出两人射击成绩与平均成绩的偏差的平方和:
刘亮:(8-7)2+(8-8)2+…+(8-9)2=6
李飞:(8-6)+(8-8)+…+(8-9)=0
李飞:(8-6)2+(8-8)2+…+(8-9)2=14
找到啦!
有区别了。
我们不如还把偏差的平方和缩小,即:
求偏差的平方和的平均数:
刘亮:[(8-7)2+(8-8)2+…+(8-9)2]÷10=0.6
李飞:[(8-6)2+(8-8)2+…+(8-9)2]÷10=1.4
刘亮的成绩与平均数的偏差比李飞的成绩与
平均数的偏差小,说明刘亮的成绩比较稳定。
一组数据中的数与这组数据的平均数的偏离程度是数据的一个重要特征,它反映了一组数据的离散程度或波动大小.
那么如何用一个特征值来反映一组数据与其平均数的离散程度呢?
设一组数据为x1,x2,…,xn,各数据与平均数
之差的平方的平均值,叫做这组数据的方差,记做
s2.
即
由此我们可以算出刘亮、李飞的射击成绩的方差分别是
s2刘亮=0.6
s2李飞=1.4
计算结果表明:
s2李飞>
s2刘亮,这说明李飞的射击成绩波动大,而刘亮的射击成绩波动小,因此刘亮的射击成绩稳定.
一般地,一组数据的方差越小,说明这组数据离散或波动的程度就越小,这组数据也就越稳定.
有两个女声合唱队,各由5名队员组成,她们的身高为(单位:厘米):
甲队:160,162,159,160,159,
乙队:180,160,150,150,160.
如果单从队员的身高考虑,哪队的演出效果好?
解:
(1)甲队队员的平均身高是
乙队的平均身高是
甲队队员身高的方差是:
乙队队员身高的方差是:
不难算出每个队的平均身高都是160厘米,但甲队身高波动小,乙队身高波动大,单从身高考虑,甲队比较整齐,演出的效果会好一些.
方差反映的是一组数据哪个方面的特征?
方差反映的是一组数据与其平均数的偏离程度,方差越小,数据越集中;方差越大,数据越分散.
甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
某同学分析上表后得出如下结论:①甲、乙两班学生成绩平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);③甲班成绩的波动比乙班大.上述结论正确的有
.
班级
参加人数
中位数
方差
平均数
甲
55
149
191
135
乙
55
151
110
135
①②③
做一做
①数据x1-3,x2-3,x3-3,…,xn-3
平均数为
,方差为
.
②数据x1+3,x2+3,x3+3,…,xn+3
平均数为
,方差为
.
若数据x1、x2、…、xn平均数为
,方差为s2,则
x
+3
x
-3
x
s2
s2
知识拓展
③数据3x1
,3x2
,3x3
,…,3xn
平均数为
,方差为
.
④数据2x1-3,2x2-3,2x3-3
,…,2xn-3
平均数为
,方差为
.
-3
2x
9s2
4s2
3x
(1)数据x1±b、x2±b、…、xn±b
平均数为
,
方差为
s2
+b
x
(2)数据ax1、ax2、…、axn
平均数为
,
方差为
a2s2
ax
1.样本方差的作用是(
)
A.表示总体的平均水平
B.表示样本的平均水平
C.准确表示总体的波动大小
D.表示样本的波动大小,从而估计总体的波动大小
D
当堂练习
2.人数相同的八年级(1)、(2)两班学生在同一次数学单元测试中,班级平均分和方差下:
,
,
,则成绩较为稳定的班级是(
)
A.甲班
B.乙班
C.两班成绩一样稳定
D.无法确定
B
3.小凯同学参加数学竞赛训练,近期的五次测试成绩得分情况如图所示,则他这五次成绩的方差
为
.
100
4.在样本方差的计算公式
中,
数字10
表示___________
,数字20表示
_______.
样本容量
平均数
5.五个数1,3,a,5,8的平均数是4,则a
=_____,这五个数的方差_____.
3
5.6
6.为了从甲、乙两名学生中选择一人去参加电脑知识竞赛,在相同条件下对他们的电脑知识进行10次测验,成绩(单位:分)如下:
甲的成绩
76
84
90
84
81
87
88
81
85
84
乙的成绩
82
86
87
90
79
81
93
90
74
78
(1)填写下表:
同学
平均成绩
中位数
众数
方差
85分以上的频率
甲
84
84
0.3
乙
84
84
34
84
90
0.5
14.4
(2)利用以上信息,请从不同的角度对甲、乙两名同学的成绩进行评价.
解:从众数看,甲成绩的众数为84分,乙成绩的众数是90分,乙的成绩比甲好;
从方差看,s2甲=14.4,
s2乙=34,甲的成绩比乙相对稳定;从甲、乙的中位数、平均数看,中位数、平均数都是84分,两人成绩一样好;
从频率看,甲85分以上的次数比乙少,乙的成绩比甲好.
课堂小结
方差
方差的统计学意义(判断数据的波动程度):
方差越大(小),数据的波动越大(小).
公式:
谢谢,请提出宝贵意见!
