人教版七年级数学下册课件:9.1.1不等式及其解集(共30张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:9.1.1不等式及其解集(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 00:00:00 | ||
图片预览







文档简介
(共30张PPT)
第九章 不等式与不等式组
9.1.1 不等式及其解集
你想过它的工作原理吗?
很多同学在假期里
去游玩,可能有在公园
里做过跷跷板,当一个
大人和一个小孩同时坐
上等臂长的跷跷板时,
两边会发生什么现象呢?
生活中的不等关系
跑步时
速度的快慢
生活中的不等关系
拔河比赛
力气的大小。
生活中的不等关系
生活中,既有相等关系,又有不等关系.
人们常用高与矮,大与小,多与少来描述不等关系。
在数学中我们用什么来描述不等关系呢?
现实生活中“不相等”处处可见,从今天起我们开始学习一类新的数学知识:不等式.
1.了解不等式及其解的概念,能准确运用不等式表示数量关系
2.理解不等式的解集及解不等式的意义;
3.能够熟练的判断不等式的解和解集,掌握在数轴上表示不等式的解集的方法.
学习目标
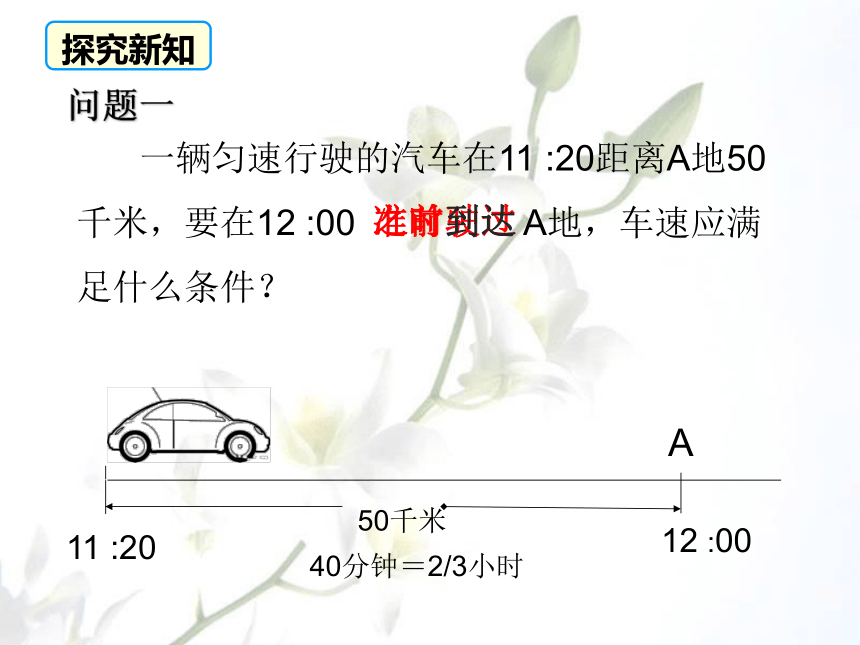
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00 A地,车速应满足什么条件?
A
50千米
问题一
11 :20
12 :00
40分钟=2/3小时
之前驶过
探究新知
准时到达
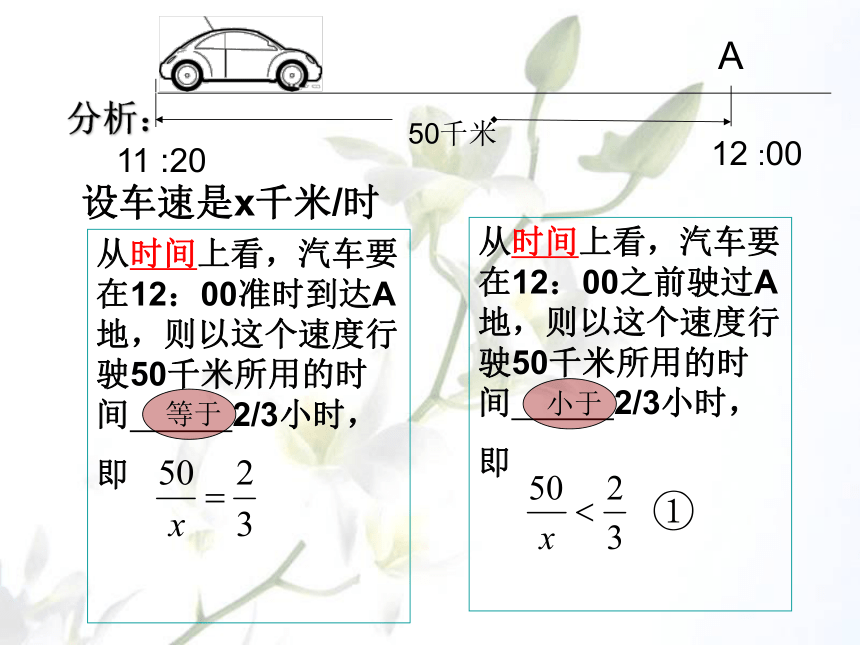
设车速是x千米/时
从时间上看,汽车要在12:00之前驶过A地,则以这个速度行驶50千米所用的时间 2/3小时,
即
①
分析:
小于
A
50千米
11 :20
12 :00
从时间上看,汽车要在12:00准时到达A地,则以这个速度行驶50千米所用的时间 2/3小时,
即
等于
设车速是x千米/时
②
分析:
A
50千米
11 :20
12 :00
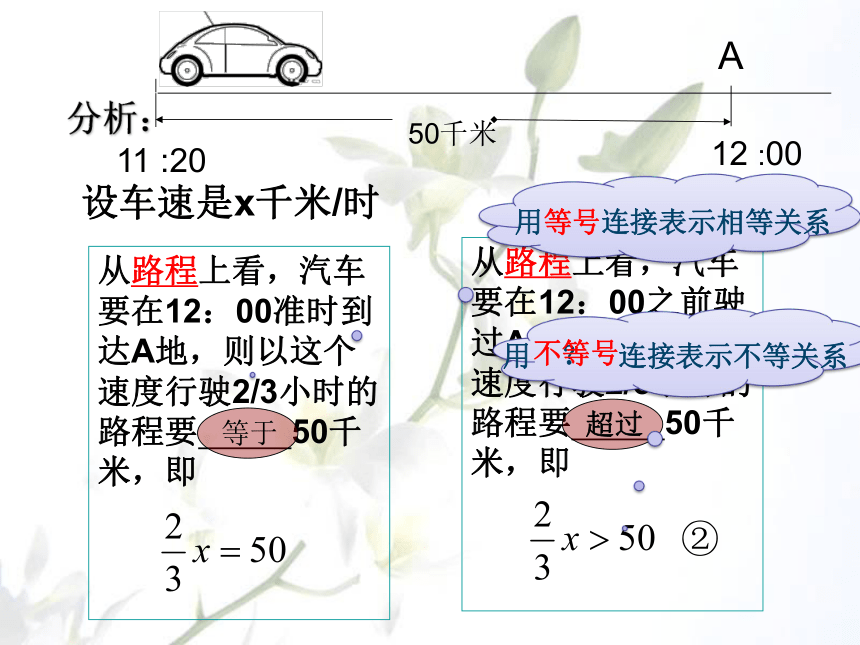
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶2/3小时的路程要 50千米,即
超过
从路程上看,汽车要在12:00准时到达A地,则以这个速度行驶2/3小时的路程要 50千米,即
等于
用 ? 连接表示不等关系
不等号
用等号连接表示相等关系
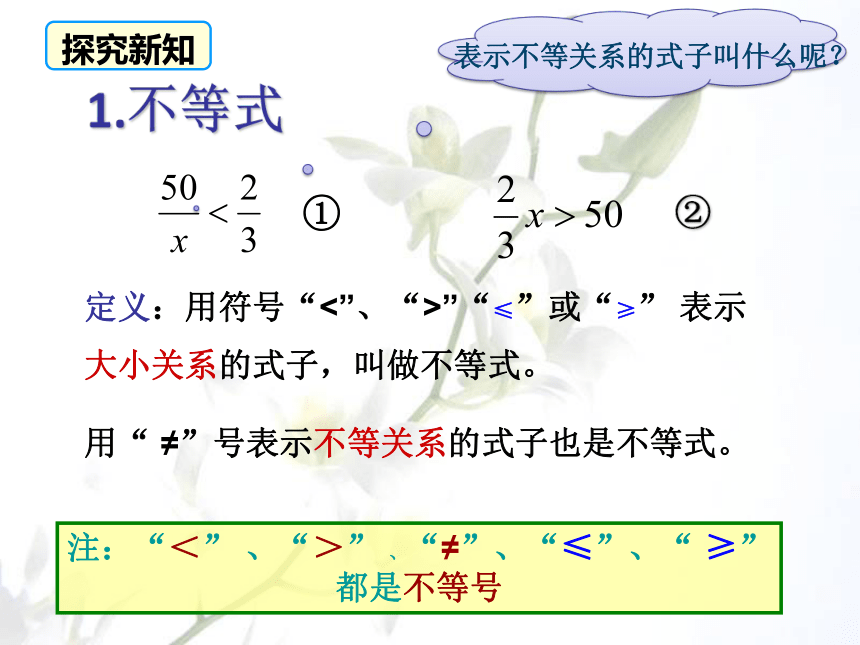
定义:用符号“<”、“>”“≤”或“≥” 表示大小关系的式子,叫做不等式。
用“ ≠”号表示不等关系的式子也是不等式。
1.不等式
①
②
注:“<” 、“>” 、“≠”、“≤”、“ ≥”都是不等号
探究新知
表示不等关系的式子叫什么呢?
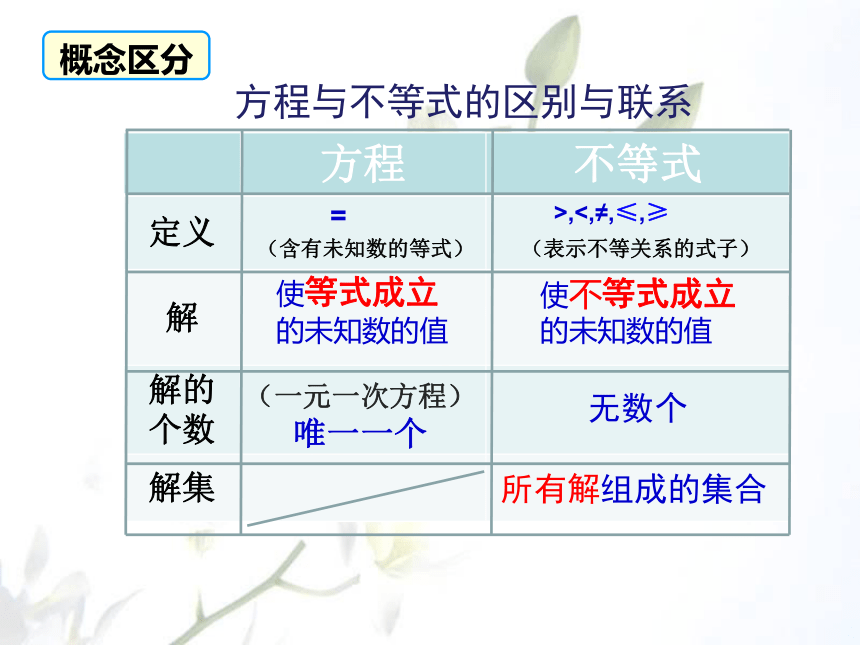
方程 不等式
定义
解
解的个数
解集
=
>,<,≠,≤,≥
使等式成立的未知数的值
使不等式成立的未知数的值
(一元一次方程)
唯一一个
所有解组成的集合
无数个
方程与不等式的区别与联系
概念区分
(含有未知数的等式)
(表示不等关系的式子)
1. 在下列表达式
① -3>0;② 4x+3y<0;③ x=3;④ x2+xy+y2;
⑤ x≠5; ⑥ x+2>y+3 ⑦ a+b=b+a ⑧
不等式有( )
A.2个 B.3个 C.5个 D.6个
解:(1) (2) (5) (6) (8),选C
不等式中可以含有未知数,也可以不含有未知数
-3>0是错误的,但它也是不等式
看式子中是否含有不等号:“>, ≥, <,≤,≠”。
辨别的关键:
练习反馈
2. 用不等式表示:
(1)a是正数
(2)a是负数
(3)a与5的和小于7
(4)a的2倍与-1的差不大于2
(5)x的 与 y的2倍的和是非正数
(6)c与4的和的20%至多是5
(7)长、宽分别为xcm,ycm的长方形的面积 小于边长为acm的正方形的面积.
a>0
a<0
a+5<7
2a+1≤-2
1
3
x + 2x≤0
1
3
20%(c + 4)≤5
“不大于”“非正数””不超过”“至多”用“≤”
思考:“不小于”“非负数”“至少”用哪个符号表示?
≥
xy < a2
3. 已知一支圆珠笔x元,签字笔与圆珠笔相比每支贵y元. 小华想要买3支圆珠笔和10支签字笔,若付50元仍找回若干元,则如何用含x,y的不等式来表示小华所需支付的金额与50元之间的关系?
解 3x+10(x+y)<50
探究二: 一辆匀速行驶的汽车在 11:20 距离A 地50千米,车速应满足什么条件使得汽车能在12:00之前到达A地?
x>50
2
3
问题:x应取哪些值才能使不等式成立?
x x x>50 成立吗?
60
63
72
75
76
90
?
2
3
2
3
不成立
不成立
不成立
不成立
成立
成立
成立
思考1:除了76和90,还有哪些值使得不等式成立?这样的值有多少个?
2:如何用式子表示这些数值?
40
42
60
48
50
76
90
90.14
75.1
830
…
解的集合
解集
x >75
2.不等式的解
能使不等式成立的未知数的值叫不等式的解.
注:1.检验某个值是否是不等式的解的方法是:代入,比较,下结论;
2.一个不等式的解不只一个(有无数个解).
探究新知
3.不等式的解集
一般地,一个含有未知数的不等式的所有的解组成这个不等式的解集。求不等式的解集的过程叫解不等式。
概念区分
不等式的解 不等式的解集
区别 定义
特点
形式
联系
使不等式成立的某个未知数的值
使不等式成立的未知数的所有的值
个体
全体
如:x=76是 的一个解
如:x > 75是 的解集
某个解是解集中
的一员
解集一定包括了
某个解
不等式的解与不等式的解集的区别与联系
想一想:
不等式的解和不等式的解集是一样的吗
不等式的解与解不等式一样吗?
4.下列说法正确的是( )
A. x=3是2x+1>5的解 B. x=3是2x+1>5的唯一解
C. x=3不是2x+1>5的解 D. x=3是2x+1>5的解集
A
5.判断下列说法是否正确?
(1) x=2是不等式x+3<4的解; ( )
(2) 不等式x+1<2的解有无穷多个; ( )
(3) x=3是不等式3x<9的解 ( )
(4) x=2是不等式3x<7的解集; ( )
×
√
×
×
(5)不等式 x+1>6的解集是 x<5; ( )
(6)x<3的正整数解只有两个 . ( )
×
√
练习反馈
不等式:
(大于75的数)
0
75
0
75
不包括75这一点,则在该点处画空心圆圈,
若包括这一点,则在该点处画实心圆点
方程:
大于向右,小于向左
数形结合思想
探究新知
你能把左边的方程的解表示到数轴上吗?
你能把右边不等式的解集表示在数轴上吗?
第一种:用不等式的最简形式 (如x>a或x第二种:用数轴表示.
用数轴表示不等式的解集的步骤: 第一步:画数轴;
第二步:定界点;
第三步:定方向.
注:大于向右画,小于向左画,
有等号(≥,≤)画实心圆点,
无等号( <, >)画空心圆圈.
探究新知
4.不等式的解集表示方法
画一画: 利用数轴来表示下列不等式的解集.
(1)x>-1 ; (2) x< .
0
-1
0
1
变式:
已知x的取值范围在数轴上表示如图,你能写出x的
取值范围吗
0
-2
x<-2
表示-1的点
表示 的点
方向向右
方向向左
空心圆圈表示不含此点
(口诀:小于向左画,大于向右画,
没等空心圈,有等实心点)
练习反馈
●
0
-1
⑵
○
0
-1
⑶
●
0
-1
⑷
○
0
-1
⑴
6.用数轴表示下列不等式的解集:
⑴ x>-1; ⑵ x≥-1; ⑶ x< -1; ⑷ x≤-1.
x>-1
x≥-1
x< -1
x≤-1
练习反馈
○
0
-3
⑴
○
0
-3
⑶
●
0
2
⑵
●
0
a
⑷
7. 写出下列数轴所表示的不等式的解集.
x > -3
x ≥ 2
x < -3
x≤ a
8.直接说出不等式的解集:
(1)x+1>2 (2)x-1 ≤3
(3)a-3≥0 (4)x+2<11
x>1
x≤4
a≥3
x<9
①什么叫不等式?举例说明。
②不等号有哪几种?
③什么叫不等式的解?什么叫解不等式?你能说出不等式x+3<4的一个解吗?
④怎样理解不等式的解集?如何在数轴上表示不等式x≥1的解集?
总结归纳
不等式的解集
数轴
解不等式
不等式
不等式的解
表
示
2、本节的思想方法
(1)类比的思想
(2)数形结合的思想
1、本节思路
方程
类
比
小 结
1. 用不等式表示下列数量关系:
(1)
(2)x比-3小
(3)两数m与n的差大于5
2.下列不是不等式5x-3<6的一个解的是( )
A.1 B.2 C.-1 D.-2
B
a+2不等于a-2
a+≠a-2
m-n >5
x <-3
达标检测
A
1
2
5
3
0
1
2
B
D
5
3
0
1
2
5
3
0
1
2
5
3
0
C
3.在数轴上表示不等式3x>5的解集,正确的是( )
A
4、图中红色部分所表示的是哪些数?你能用不等式表示这个区域吗?
0
-1
1
5、请说出一个不等式,使得3是它的一个解,而4不是它的解。
6、请直接想出下列不等式的解集,并在数轴上表示。
(1) 2x<8 (2)x-2>0
X<1
8.有下列数学表达式:
①-1<0;
②3m-2n>0;
③x=4;
④x≠7;
⑤5x+4=x+5;
其中是不等式的有 ( )
⑥x2+xy+y2;
⑦x+2>y+3;
⑧x2>4;
⑨3x-2>4x-3;
⑩3+5<7;
①②④⑦⑧⑨⑩
7.直接写出下列不等式的解集.
x+3>6的解集是 ;
2x<8的解集是 ;
x-2>0的解集是 .
x>3
x<4
x>2
9. 判断下列说法是否正确:
(1)x = -1是不等式x < 1的一个解
(2)x = 2是不等式x – 1 > 0的解集
(3)不等式x + 3 >6的解集是x>3
(4)不等式1 – x < 0的解有无数多个数
(5)x – 5 < 1的解是x = 2
(6)x = 0是不等式x ≤0的解
10.不等式x<5有多少个解?有多少个正整数解?
不等式x<5有无数个解;有4个正整数解,分别是4,3,2,1。
第九章 不等式与不等式组
9.1.1 不等式及其解集
你想过它的工作原理吗?
很多同学在假期里
去游玩,可能有在公园
里做过跷跷板,当一个
大人和一个小孩同时坐
上等臂长的跷跷板时,
两边会发生什么现象呢?
生活中的不等关系
跑步时
速度的快慢
生活中的不等关系
拔河比赛
力气的大小。
生活中的不等关系
生活中,既有相等关系,又有不等关系.
人们常用高与矮,大与小,多与少来描述不等关系。
在数学中我们用什么来描述不等关系呢?
现实生活中“不相等”处处可见,从今天起我们开始学习一类新的数学知识:不等式.
1.了解不等式及其解的概念,能准确运用不等式表示数量关系
2.理解不等式的解集及解不等式的意义;
3.能够熟练的判断不等式的解和解集,掌握在数轴上表示不等式的解集的方法.
学习目标
一辆匀速行驶的汽车在11 :20距离A地50千米,要在12 :00 A地,车速应满足什么条件?
A
50千米
问题一
11 :20
12 :00
40分钟=2/3小时
之前驶过
探究新知
准时到达
设车速是x千米/时
从时间上看,汽车要在12:00之前驶过A地,则以这个速度行驶50千米所用的时间 2/3小时,
即
①
分析:
小于
A
50千米
11 :20
12 :00
从时间上看,汽车要在12:00准时到达A地,则以这个速度行驶50千米所用的时间 2/3小时,
即
等于
设车速是x千米/时
②
分析:
A
50千米
11 :20
12 :00
从路程上看,汽车要在12:00之前驶过A地,则以这个速度行驶2/3小时的路程要 50千米,即
超过
从路程上看,汽车要在12:00准时到达A地,则以这个速度行驶2/3小时的路程要 50千米,即
等于
用 ? 连接表示不等关系
不等号
用等号连接表示相等关系
定义:用符号“<”、“>”“≤”或“≥” 表示大小关系的式子,叫做不等式。
用“ ≠”号表示不等关系的式子也是不等式。
1.不等式
①
②
注:“<” 、“>” 、“≠”、“≤”、“ ≥”都是不等号
探究新知
表示不等关系的式子叫什么呢?
方程 不等式
定义
解
解的个数
解集
=
>,<,≠,≤,≥
使等式成立的未知数的值
使不等式成立的未知数的值
(一元一次方程)
唯一一个
所有解组成的集合
无数个
方程与不等式的区别与联系
概念区分
(含有未知数的等式)
(表示不等关系的式子)
1. 在下列表达式
① -3>0;② 4x+3y<0;③ x=3;④ x2+xy+y2;
⑤ x≠5; ⑥ x+2>y+3 ⑦ a+b=b+a ⑧
不等式有( )
A.2个 B.3个 C.5个 D.6个
解:(1) (2) (5) (6) (8),选C
不等式中可以含有未知数,也可以不含有未知数
-3>0是错误的,但它也是不等式
看式子中是否含有不等号:“>, ≥, <,≤,≠”。
辨别的关键:
练习反馈
2. 用不等式表示:
(1)a是正数
(2)a是负数
(3)a与5的和小于7
(4)a的2倍与-1的差不大于2
(5)x的 与 y的2倍的和是非正数
(6)c与4的和的20%至多是5
(7)长、宽分别为xcm,ycm的长方形的面积 小于边长为acm的正方形的面积.
a>0
a<0
a+5<7
2a+1≤-2
1
3
x + 2x≤0
1
3
20%(c + 4)≤5
“不大于”“非正数””不超过”“至多”用“≤”
思考:“不小于”“非负数”“至少”用哪个符号表示?
≥
xy < a2
3. 已知一支圆珠笔x元,签字笔与圆珠笔相比每支贵y元. 小华想要买3支圆珠笔和10支签字笔,若付50元仍找回若干元,则如何用含x,y的不等式来表示小华所需支付的金额与50元之间的关系?
解 3x+10(x+y)<50
探究二: 一辆匀速行驶的汽车在 11:20 距离A 地50千米,车速应满足什么条件使得汽车能在12:00之前到达A地?
x>50
2
3
问题:x应取哪些值才能使不等式成立?
x x x>50 成立吗?
60
63
72
75
76
90
?
2
3
2
3
不成立
不成立
不成立
不成立
成立
成立
成立
思考1:除了76和90,还有哪些值使得不等式成立?这样的值有多少个?
2:如何用式子表示这些数值?
40
42
60
48
50
76
90
90.14
75.1
830
…
解的集合
解集
x >75
2.不等式的解
能使不等式成立的未知数的值叫不等式的解.
注:1.检验某个值是否是不等式的解的方法是:代入,比较,下结论;
2.一个不等式的解不只一个(有无数个解).
探究新知
3.不等式的解集
一般地,一个含有未知数的不等式的所有的解组成这个不等式的解集。求不等式的解集的过程叫解不等式。
概念区分
不等式的解 不等式的解集
区别 定义
特点
形式
联系
使不等式成立的某个未知数的值
使不等式成立的未知数的所有的值
个体
全体
如:x=76是 的一个解
如:x > 75是 的解集
某个解是解集中
的一员
解集一定包括了
某个解
不等式的解与不等式的解集的区别与联系
想一想:
不等式的解和不等式的解集是一样的吗
不等式的解与解不等式一样吗?
4.下列说法正确的是( )
A. x=3是2x+1>5的解 B. x=3是2x+1>5的唯一解
C. x=3不是2x+1>5的解 D. x=3是2x+1>5的解集
A
5.判断下列说法是否正确?
(1) x=2是不等式x+3<4的解; ( )
(2) 不等式x+1<2的解有无穷多个; ( )
(3) x=3是不等式3x<9的解 ( )
(4) x=2是不等式3x<7的解集; ( )
×
√
×
×
(5)不等式 x+1>6的解集是 x<5; ( )
(6)x<3的正整数解只有两个 . ( )
×
√
练习反馈
不等式:
(大于75的数)
0
75
0
75
不包括75这一点,则在该点处画空心圆圈,
若包括这一点,则在该点处画实心圆点
方程:
大于向右,小于向左
数形结合思想
探究新知
你能把左边的方程的解表示到数轴上吗?
你能把右边不等式的解集表示在数轴上吗?
第一种:用不等式的最简形式 (如x>a或x
用数轴表示不等式的解集的步骤: 第一步:画数轴;
第二步:定界点;
第三步:定方向.
注:大于向右画,小于向左画,
有等号(≥,≤)画实心圆点,
无等号( <, >)画空心圆圈.
探究新知
4.不等式的解集表示方法
画一画: 利用数轴来表示下列不等式的解集.
(1)x>-1 ; (2) x< .
0
-1
0
1
变式:
已知x的取值范围在数轴上表示如图,你能写出x的
取值范围吗
0
-2
x<-2
表示-1的点
表示 的点
方向向右
方向向左
空心圆圈表示不含此点
(口诀:小于向左画,大于向右画,
没等空心圈,有等实心点)
练习反馈
●
0
-1
⑵
○
0
-1
⑶
●
0
-1
⑷
○
0
-1
⑴
6.用数轴表示下列不等式的解集:
⑴ x>-1; ⑵ x≥-1; ⑶ x< -1; ⑷ x≤-1.
x>-1
x≥-1
x< -1
x≤-1
练习反馈
○
0
-3
⑴
○
0
-3
⑶
●
0
2
⑵
●
0
a
⑷
7. 写出下列数轴所表示的不等式的解集.
x > -3
x ≥ 2
x < -3
x≤ a
8.直接说出不等式的解集:
(1)x+1>2 (2)x-1 ≤3
(3)a-3≥0 (4)x+2<11
x>1
x≤4
a≥3
x<9
①什么叫不等式?举例说明。
②不等号有哪几种?
③什么叫不等式的解?什么叫解不等式?你能说出不等式x+3<4的一个解吗?
④怎样理解不等式的解集?如何在数轴上表示不等式x≥1的解集?
总结归纳
不等式的解集
数轴
解不等式
不等式
不等式的解
表
示
2、本节的思想方法
(1)类比的思想
(2)数形结合的思想
1、本节思路
方程
类
比
小 结
1. 用不等式表示下列数量关系:
(1)
(2)x比-3小
(3)两数m与n的差大于5
2.下列不是不等式5x-3<6的一个解的是( )
A.1 B.2 C.-1 D.-2
B
a+2不等于a-2
a+≠a-2
m-n >5
x <-3
达标检测
A
1
2
5
3
0
1
2
B
D
5
3
0
1
2
5
3
0
1
2
5
3
0
C
3.在数轴上表示不等式3x>5的解集,正确的是( )
A
4、图中红色部分所表示的是哪些数?你能用不等式表示这个区域吗?
0
-1
1
5、请说出一个不等式,使得3是它的一个解,而4不是它的解。
6、请直接想出下列不等式的解集,并在数轴上表示。
(1) 2x<8 (2)x-2>0
X<1
8.有下列数学表达式:
①-1<0;
②3m-2n>0;
③x=4;
④x≠7;
⑤5x+4=x+5;
其中是不等式的有 ( )
⑥x2+xy+y2;
⑦x+2>y+3;
⑧x2>4;
⑨3x-2>4x-3;
⑩3+5<7;
①②④⑦⑧⑨⑩
7.直接写出下列不等式的解集.
x+3>6的解集是 ;
2x<8的解集是 ;
x-2>0的解集是 .
x>3
x<4
x>2
9. 判断下列说法是否正确:
(1)x = -1是不等式x < 1的一个解
(2)x = 2是不等式x – 1 > 0的解集
(3)不等式x + 3 >6的解集是x>3
(4)不等式1 – x < 0的解有无数多个数
(5)x – 5 < 1的解是x = 2
(6)x = 0是不等式x ≤0的解
10.不等式x<5有多少个解?有多少个正整数解?
不等式x<5有无数个解;有4个正整数解,分别是4,3,2,1。
