湘教版七年级数学下册第6章数据的分析章末复习课件(共24张PPT)
文档属性
| 名称 | 湘教版七年级数学下册第6章数据的分析章末复习课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 15:20:03 | ||
图片预览





文档简介
(共24张PPT)
章末复习
湘教版
七年级下册
要点梳理
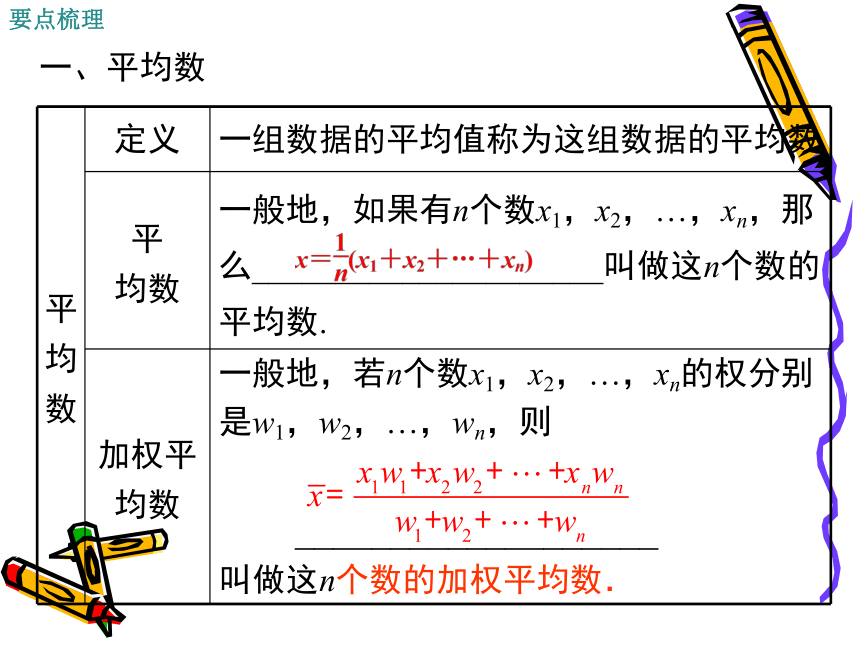
一、平均数
平均数
定义
一组数据的平均值称为这组数据的平均数
平
均数
一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这n个数的平均数.
加权平
均数
一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
___________________
叫做这n个数的加权平均数.
最多
中间位置的数
两个数据的平均数
中位数
定义
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错
提醒
确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众
数
定义
一组数据中出现次数________的数据叫做这组数据的众数
防错
提醒
(1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
二、方差
平均数
大
表示波
动的量
定义
意义
方差
设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2
方差越大,数据的波动越___,反之也成立
考点讲练
考点一
平均数、中位数、众数
例1
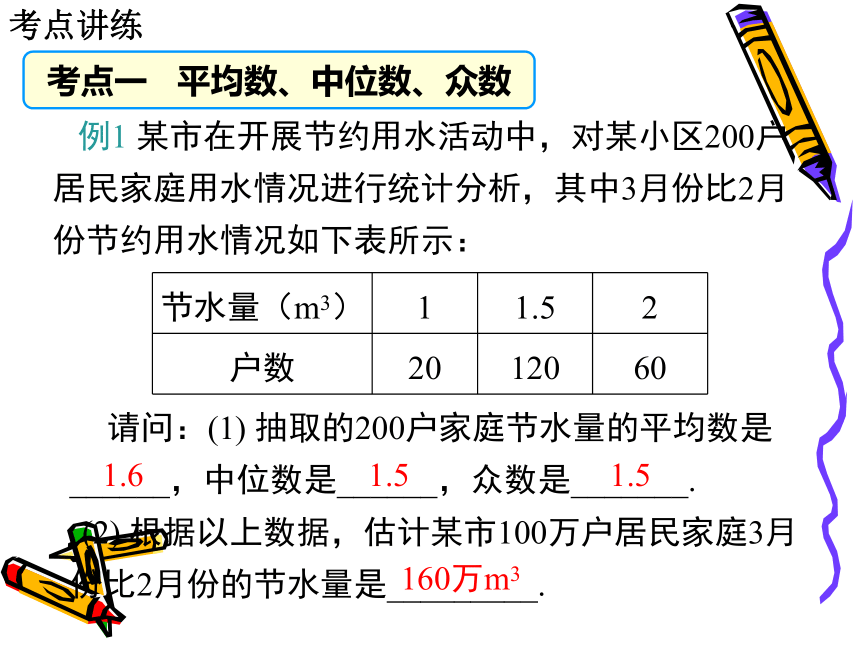
某市在开展节约用水活动中,对某小区200户居民家庭用水情况进行统计分析,其中3月份比2月份节约用水情况如下表所示:
节水量(m3)
1
1.5
2
户数
20
120
60
请问:(1)
抽取的200户家庭节水量的平均数是______,中位数是______,众数是_______.
(2)
根据以上数据,估计某市100万户居民家庭3月份比2月份的节水量是_________.
1.6
1.5
160万m3
1.5
1.某米店经营某种品牌的大米,该店记录了一周中不同包装(10
kg,20
kg,50
kg)的大米的销售量(单位:袋)如下:10
kg装100袋;20
kg装220袋;
50
kg装80袋.如果每500
g大米的进价和售价都相同,则他最应该关注的是这些销售数据(袋数)中的(
)
A.平均数
B.中位数
C.众数
D.最大值
C
针对训练
A
2.一组数据中的一个数大小发生了变化,一定会
影响这组数据的平均数、众数、中位数中的(
)
A.1个
B.2个 C.3个 D.0个
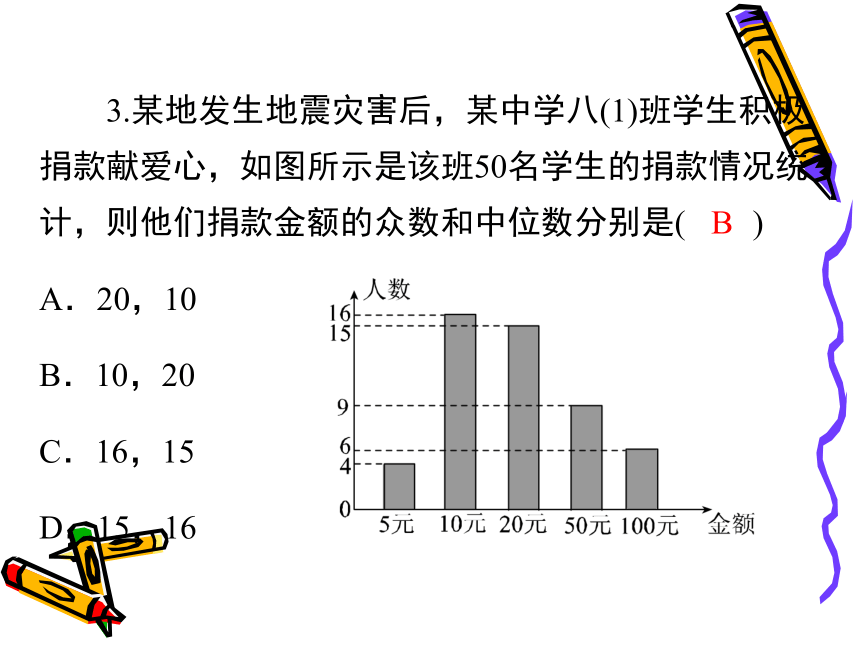
3.某地发生地震灾害后,某中学八(1)班学生积极捐款献爱心,如图所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A.20,10
B.10,20
C.16,15
D.15,16
B
4.
小刚在“中国梦·我的梦”演讲比赛中,演讲内容、语言表达、演讲技能、形象礼仪四项得分依次为9.8,9.4,9.2,9.3.
若其综合得分按演讲内容50%、语言表达20%、演讲技能20%、形象礼仪10%的比例计算,则他的综合得分是_________.
9.55
考点二
方差的计算及应用
例2
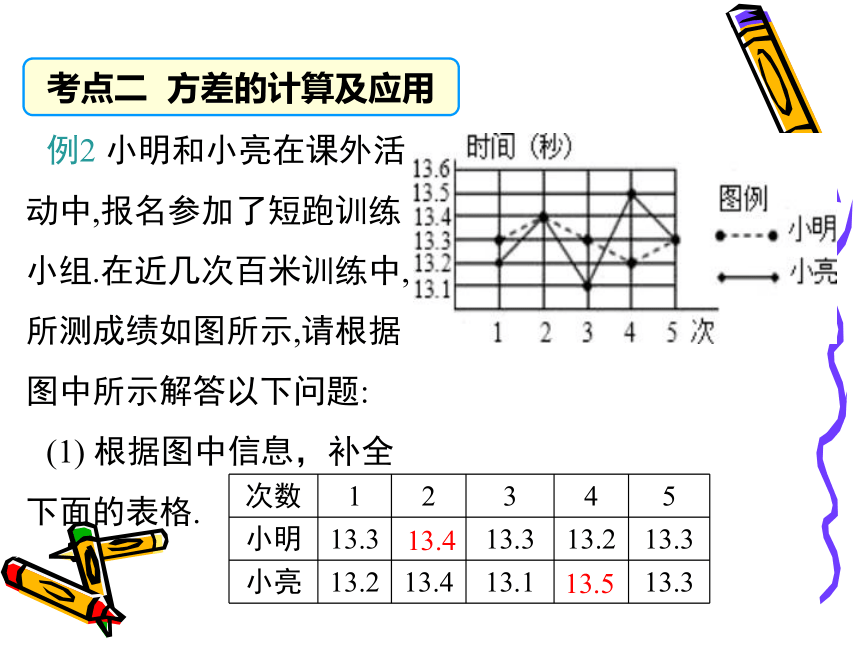
小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题:
(1)
根据图中信息,补全下面的表格.
次数
1
2
3
4
5
小明
13.3
13.3
13.2
13.3
小亮
13.2
13.4
13.1
13.3
13.4
13.5
(2)
分别计算成绩的平均数
和方差,填入表格.
若你是
老师,将小明与小亮的成绩
比较析后,
将分别给予他们
怎样的建议?
平均数
方差
小明
小亮
13.3
13.3
0.02
0.004
解:从平均数看,两人的平均水平相同;从方差看,小明的成绩较稳定,小亮的成绩波动较大.
给小明的建议是:加强锻炼,提高爆发力,提升短跑成绩;
给小亮的建议是:总结经验,找出成绩忽高忽低的原因,在稳定中提高.
平均数
方差
小明
小亮
13.3
13.3
0.02
0.004
针对训练
5.小张和小李去练习射击,第一轮10发子弹打完后,两人的成绩如图.根据图中的信息,小张小李两人中成绩较稳定的是
.
小张
例3
我市某中学七、八年级各选派10名选手参加学校举办的“爱我祖国”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
考点三
分析数据做决策
队别
平均分
中位数
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
(1)解:依题意,得
解得
(2)m=6,n=20%.
(3)①八年级队平均分高于七年级队;
②八年级队的成绩比七年级队稳定;
③八年级队的成绩集中在中上游,所以支持八年级队成绩好(注:任说两条即可).
(3×1+6a+7×1+8×1+9×1+10b)÷10=6.7
1+a+1+1+1+b=10
a=5,
b=1.
1、在一次英语口试中,10名学生的得分如下:80、70、90、100、80、60、80、70、90、100,则这次英语口试中,学生得分的众数是(
)
2、八年级一班46个同学中,13岁的有5人,14岁的20人,15岁的有15人,16岁
的有6人。八年级一班学生年龄的平均分,中位数,众数分别是(
)
3、有7个数由小到大依次排列,平均数是38,如果这组数的前4个数的平均数是33,后4个数的平均数是42,这7个数的中位数是(
)
随堂练习
4、设一组数据为a、b、c、d、a、c、d、d、a,其中a<b<c<d,则这组数据的中位数是(
)
A、a
B、b
C、c、
D、d
5、已知一组数据x、-5、4、-3、2、-5;根据下列条件确定x的值;
(1)中位数为-1;
(2)平均数是3;
(3)x是唯一的众数;
6、某广告公司欲招聘广告策划人员一名,对A、B、C三名候选人进行了三项素质测试,他们各项测试成绩如下表所示:
预测项目
A
B
C
创新
72
85
67
综合知识
50
74
70
语言
88
45
67
(1)如果根据三项测试的平均成绩确定采用人选,那么谁将录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按4︰3︰1的比例确定各人的成绩,此时谁将录用?
(3)若要让最后的测试成绩从高到低为A、C、B,则权重可能是多少?
7、为了解某校八年级学生成长发肓情况,从全校八年级学生中随机抽取了100人测量体重,他们的体重频数分布表如下:
体重
45~49
50
~54
55
~59
60
~64
65
~69
70
~74
75
~79
80
~84
频数
5
22
35
20
8
6
3
1
问:学校八年级学生的平均体重是多少?
8、
某次考试后,政治老师对试卷中第36题(注:满分4分)进行了统计,并根据统计结果绘出如图所示的得分情况统计
表。得分率=得该分数的人数/被统计的人数。
0
1
2
3
4
34.8%
10%
25.8%
9.8%
19.6%
分数
(分)
得分率
(1)老师估计该题能得2分或2分以上者,即可认为“比较好”,
在所统计的学生中共有224人不属于“比
较
好”。问统计的总人数为多少?
(2)求该题得分的众数、中位数
和平均数。
9、
数学老师布置10道选择题,课代表将全班同学的答题情况绘制成条形统计图,根据图表,全班每位同学答对的题数的中位数和众数分别为(
)
学生数
答对题数
D
A
8,8
B
8,9
C
9,9
D
9,8
4
20
18
8
10、某中学要召开运动会,决定从九年级的150名女生中选30人,组成一个彩旗方队。现在抽测了10名女生的身高,结果如下(单位:厘米):166,154,151,167,162,158,158,160,162,162。
(1)依据样本数据估计该九年级全体女生的平均身高约是多少?
(2)这10名女生的身高的中位数、众数各是多少?
(3)请你依据样本数据,设计一个挑选参加方队的女生的方案。
通过这节课的学习活动,你有什么收获?
课堂小结
谢谢,请提出宝贵意见!
章末复习
湘教版
七年级下册
要点梳理
一、平均数
平均数
定义
一组数据的平均值称为这组数据的平均数
平
均数
一般地,如果有n个数x1,x2,…,xn,那么_____________________叫做这n个数的平均数.
加权平
均数
一般地,若n个数x1,x2,…,xn的权分别
是w1,w2,…,wn,则
___________________
叫做这n个数的加权平均数.
最多
中间位置的数
两个数据的平均数
中位数
定义
将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错
提醒
确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众
数
定义
一组数据中出现次数________的数据叫做这组数据的众数
防错
提醒
(1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
二、方差
平均数
大
表示波
动的量
定义
意义
方差
设有n个数据x1,x2,x3,…,xn,各数据与它们的________的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2
方差越大,数据的波动越___,反之也成立
考点讲练
考点一
平均数、中位数、众数
例1
某市在开展节约用水活动中,对某小区200户居民家庭用水情况进行统计分析,其中3月份比2月份节约用水情况如下表所示:
节水量(m3)
1
1.5
2
户数
20
120
60
请问:(1)
抽取的200户家庭节水量的平均数是______,中位数是______,众数是_______.
(2)
根据以上数据,估计某市100万户居民家庭3月份比2月份的节水量是_________.
1.6
1.5
160万m3
1.5
1.某米店经营某种品牌的大米,该店记录了一周中不同包装(10
kg,20
kg,50
kg)的大米的销售量(单位:袋)如下:10
kg装100袋;20
kg装220袋;
50
kg装80袋.如果每500
g大米的进价和售价都相同,则他最应该关注的是这些销售数据(袋数)中的(
)
A.平均数
B.中位数
C.众数
D.最大值
C
针对训练
A
2.一组数据中的一个数大小发生了变化,一定会
影响这组数据的平均数、众数、中位数中的(
)
A.1个
B.2个 C.3个 D.0个
3.某地发生地震灾害后,某中学八(1)班学生积极捐款献爱心,如图所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是( )
A.20,10
B.10,20
C.16,15
D.15,16
B
4.
小刚在“中国梦·我的梦”演讲比赛中,演讲内容、语言表达、演讲技能、形象礼仪四项得分依次为9.8,9.4,9.2,9.3.
若其综合得分按演讲内容50%、语言表达20%、演讲技能20%、形象礼仪10%的比例计算,则他的综合得分是_________.
9.55
考点二
方差的计算及应用
例2
小明和小亮在课外活动中,报名参加了短跑训练小组.在近几次百米训练中,所测成绩如图所示,请根据图中所示解答以下问题:
(1)
根据图中信息,补全下面的表格.
次数
1
2
3
4
5
小明
13.3
13.3
13.2
13.3
小亮
13.2
13.4
13.1
13.3
13.4
13.5
(2)
分别计算成绩的平均数
和方差,填入表格.
若你是
老师,将小明与小亮的成绩
比较析后,
将分别给予他们
怎样的建议?
平均数
方差
小明
小亮
13.3
13.3
0.02
0.004
解:从平均数看,两人的平均水平相同;从方差看,小明的成绩较稳定,小亮的成绩波动较大.
给小明的建议是:加强锻炼,提高爆发力,提升短跑成绩;
给小亮的建议是:总结经验,找出成绩忽高忽低的原因,在稳定中提高.
平均数
方差
小明
小亮
13.3
13.3
0.02
0.004
针对训练
5.小张和小李去练习射击,第一轮10发子弹打完后,两人的成绩如图.根据图中的信息,小张小李两人中成绩较稳定的是
.
小张
例3
我市某中学七、八年级各选派10名选手参加学校举办的“爱我祖国”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
考点三
分析数据做决策
队别
平均分
中位数
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
(1)解:依题意,得
解得
(2)m=6,n=20%.
(3)①八年级队平均分高于七年级队;
②八年级队的成绩比七年级队稳定;
③八年级队的成绩集中在中上游,所以支持八年级队成绩好(注:任说两条即可).
(3×1+6a+7×1+8×1+9×1+10b)÷10=6.7
1+a+1+1+1+b=10
a=5,
b=1.
1、在一次英语口试中,10名学生的得分如下:80、70、90、100、80、60、80、70、90、100,则这次英语口试中,学生得分的众数是(
)
2、八年级一班46个同学中,13岁的有5人,14岁的20人,15岁的有15人,16岁
的有6人。八年级一班学生年龄的平均分,中位数,众数分别是(
)
3、有7个数由小到大依次排列,平均数是38,如果这组数的前4个数的平均数是33,后4个数的平均数是42,这7个数的中位数是(
)
随堂练习
4、设一组数据为a、b、c、d、a、c、d、d、a,其中a<b<c<d,则这组数据的中位数是(
)
A、a
B、b
C、c、
D、d
5、已知一组数据x、-5、4、-3、2、-5;根据下列条件确定x的值;
(1)中位数为-1;
(2)平均数是3;
(3)x是唯一的众数;
6、某广告公司欲招聘广告策划人员一名,对A、B、C三名候选人进行了三项素质测试,他们各项测试成绩如下表所示:
预测项目
A
B
C
创新
72
85
67
综合知识
50
74
70
语言
88
45
67
(1)如果根据三项测试的平均成绩确定采用人选,那么谁将录用?
(2)根据实际需要,公司将创新、综合知识、语言三项测试得分按4︰3︰1的比例确定各人的成绩,此时谁将录用?
(3)若要让最后的测试成绩从高到低为A、C、B,则权重可能是多少?
7、为了解某校八年级学生成长发肓情况,从全校八年级学生中随机抽取了100人测量体重,他们的体重频数分布表如下:
体重
45~49
50
~54
55
~59
60
~64
65
~69
70
~74
75
~79
80
~84
频数
5
22
35
20
8
6
3
1
问:学校八年级学生的平均体重是多少?
8、
某次考试后,政治老师对试卷中第36题(注:满分4分)进行了统计,并根据统计结果绘出如图所示的得分情况统计
表。得分率=得该分数的人数/被统计的人数。
0
1
2
3
4
34.8%
10%
25.8%
9.8%
19.6%
分数
(分)
得分率
(1)老师估计该题能得2分或2分以上者,即可认为“比较好”,
在所统计的学生中共有224人不属于“比
较
好”。问统计的总人数为多少?
(2)求该题得分的众数、中位数
和平均数。
9、
数学老师布置10道选择题,课代表将全班同学的答题情况绘制成条形统计图,根据图表,全班每位同学答对的题数的中位数和众数分别为(
)
学生数
答对题数
D
A
8,8
B
8,9
C
9,9
D
9,8
4
20
18
8
10、某中学要召开运动会,决定从九年级的150名女生中选30人,组成一个彩旗方队。现在抽测了10名女生的身高,结果如下(单位:厘米):166,154,151,167,162,158,158,160,162,162。
(1)依据样本数据估计该九年级全体女生的平均身高约是多少?
(2)这10名女生的身高的中位数、众数各是多少?
(3)请你依据样本数据,设计一个挑选参加方队的女生的方案。
通过这节课的学习活动,你有什么收获?
课堂小结
谢谢,请提出宝贵意见!
