黑龙江省哈尔滨市第十七中学2019-2020学年度第二学期八年级五月份数学测试题(含答案 答题卡)
文档属性
| 名称 | 黑龙江省哈尔滨市第十七中学2019-2020学年度第二学期八年级五月份数学测试题(含答案 答题卡) |  | |
| 格式 | zip | ||
| 文件大小 | 814.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-06-11 13:34:50 | ||
图片预览


文档简介
哈尔滨市第十七中学校
2019--2020
学年度(下)
八年级五月份质量检测数学试卷
温馨提示:亲爱的同学们,病毒无情,人有情,这份试卷再次记录着你的成长,请相信自己,认真审题,看清要求,仔细答卷。祝你成功!
一、选择题(每题
3
分,共
30
分)
1.下列各图中表示
y
是
x
的函数图像的是(
)
2.下列各组线段中,能构成直角三角形的是(
)
A.2,3,4
B.3,4,6
C.5,12,13
D.
4,6,7
3.如图,四边形
ABCD
为平行四边形,作∠BAD
的平分线,交
DC
边于点
E,
若∠DEA=30°,则∠B
的度数为(
)
A.100°
B.120°
C.135°
D.150°
4.一次函数
y=kx+b
的图象经过第一、三、四象限,则(
)
A.
k>0,b>0
B.
k>0,b<0
C.
k<0,b>0
D.
k<0,b<0
5.下列性质中,矩形具有而一般的平行四边形不具有的特点是(
)
A.对边相等
B.对角相等
C.对角线相等
D.对边平行
6.
若
a
b
c
0
,则一元二次方程
ax2
bx
c
0(a
0)
必有一根是(
)
A.0
B.1
C.
-1
D.
无法确定
7.如图,已知□ABCD
的面积为
48,E
为
AB
的中点,连接
DE,则△ODE
的面积为(
).
A.8
B.6
C.4
D.3
7
题
8
题
9
题
8.如图,矩形
ABCD
中,AB=8,AD=6,折叠纸片,使边
AD
落在对角线
BD
上,点
A
对应点
E,折痕为
DG,则
DG
长为(
)
A.
3
B.5
C.
D.
9.
如图,函数
y=2x
和
y=ax+4
的图象相交于点
A(m,3),则不等式
2x<ax+4
的解集为(
)
A.
x
3
2
B.x<3
C.
x
3
2
D.x>3
10.仁爱药店在“抗疫”期间销售一种消毒液,如果一次购买
10
瓶以上(不含
10
瓶),超过
10
瓶的那部分的价格将打折,并依此得到付款金额
y(单位:元)与一次购买消毒液数量
x(单位:瓶)之间的函数关系如图所示.下列四种说法:其中正确的个数是(
)
①一次购买消毒液数量不超过
10
瓶时,销售价格为
5
元/瓶;
②一次购买
30
瓶时,付款金额为
100
元;
③一次购买
10
瓶以上时,超过
10
瓶的那部分消毒液的价格打七折;
④一次购买
40
瓶消毒液比分两次购买且每次购买
20
瓶消毒液少花
25
元钱.
A.1
B.2
C.3
D.4
二、填空题(每题
3
分,共
30
分)
10
题
x
11.函数
y=
2x
3
中自变量
x
的取值范围是
。
12.当
a
=
时,(a
3)x
a
1
x
5是关于
x
的一元二次方程
。
13.
在
Rt△ABC
中,CD
斜边
AB
上的高,若
AB=10,AC:BC=3:4,则
CD=
.
(
2
)14.如图,四边形
ABCD
中,BD⊥DC
于点
D,∠DCB=45°,∠ABD=∠ECD,点
F
是
BC
的中点,已知
BD=
2
,则
FE
的长是
.
14
题
16
题
17
题
15.已知点(-6,m),(8,n)都在直线
y=-x-b
上,则
m
n。(填大小关系)
16.
如图坐标系,四边形
ABCD
为菱形,顶点
A、B
在
x
轴上,AB=5,点
C
在第一象限,且菱形
ABCD
的面积为
20,
A
坐标为(-2,0),则顶点
C
的坐标为
17.如图,矩形
ABCD
的对角线相交于点
O,OF⊥BC,CE⊥BD,
OE∶BE=1∶3,OF=4,则线段
BD
的长为
.
18.如图,△ABC
中,AD⊥BC
于
D,F
为△ABC
外一点,
连
DF
交
AB
于
E,∠FBD=∠FDA=∠C,FD=AD=4,
BC=8,则△ADE
与△BFE
的面积差为
。
18
题
19.已知菱形
ABCD
的边长为
6,∠A=60°,如果点
P
是菱形
(
3
)内一点,且
PB=PD=2
,那么
AP
的长为
。
20.如图∠BAC=90°,∠ABC=2∠CAD,∠ADE=45°,
9
BE=
2
,CD=1,则
BC=
。
20
题
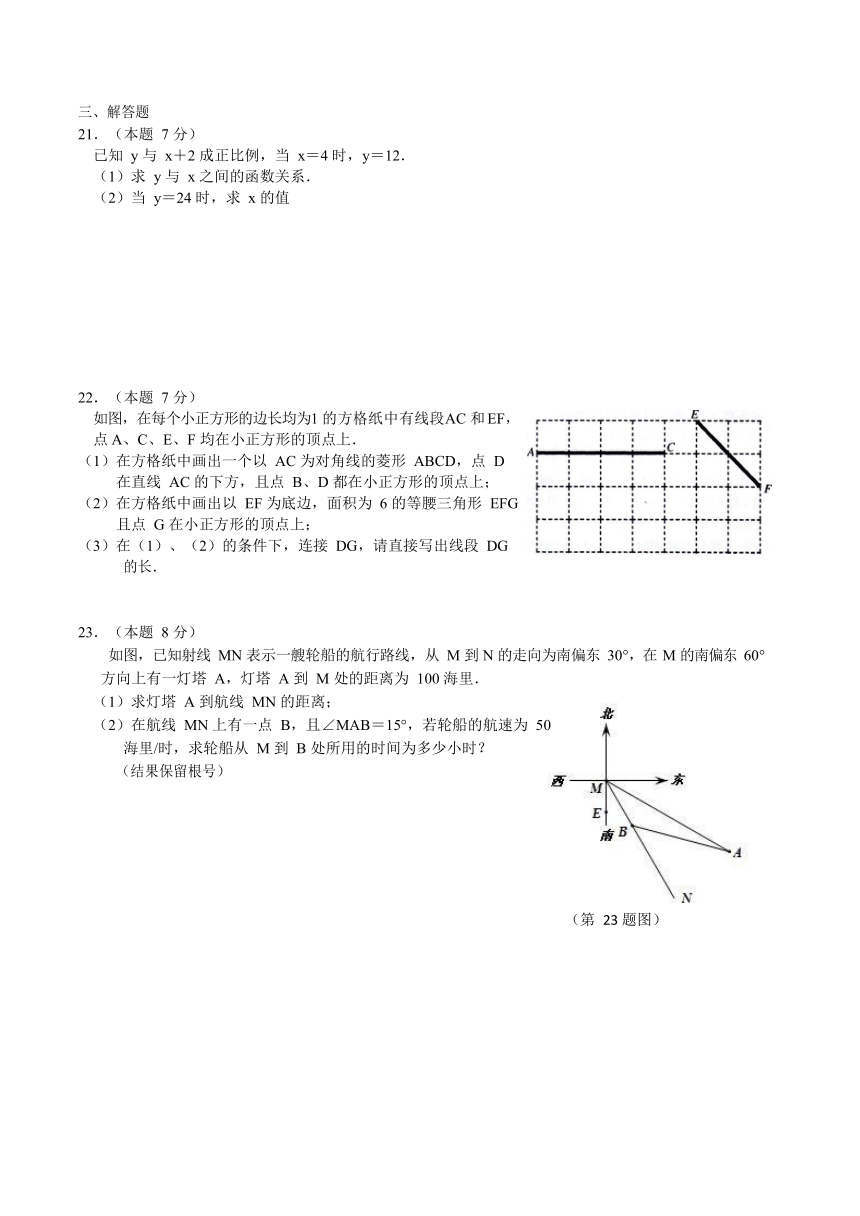
三、解答题
21.(本题
7
分)
已知
y
与
x+2
成正比例,当
x=4
时,y=12.
(1)求
y
与
x
之间的函数关系.
(2)当
y=24
时,求
x
的值
22.(本题
7
分)
如图,在每个小正方形的边长均为1
的方格纸中有线段AC
和EF,
点
A、C、E、F
均在小正方形的顶点上.
(1)在方格纸中画出一个以
AC
为对角线的菱形
ABCD,点
D
在直线
AC
的下方,且点
B、D
都在小正方形的顶点上;
(2)在方格纸中画出以
EF
为底边,面积为
6
的等腰三角形
EFG
且点
G
在小正方形的顶点上;
(3)在(1)、(2)的条件下,连接
DG,请直接写出线段
DG
的长.
23.(本题
8
分)
如图,已知射线
MN
表示一艘轮船的航行路线,从
M
到
N
的走向为南偏东
30°,在
M
的南偏东
60°
方向上有一灯塔
A,灯塔
A
到
M
处的距离为
100
海里.
(1)求灯塔
A
到航线
MN
的距离;
(2)在航线
MN
上有一点
B,且∠MAB=15°,若轮船的航速为
50
海里/时,求轮船从
M
到
B
处所用的时间为多少小时?
(结果保留根号)
(第
23
题图)
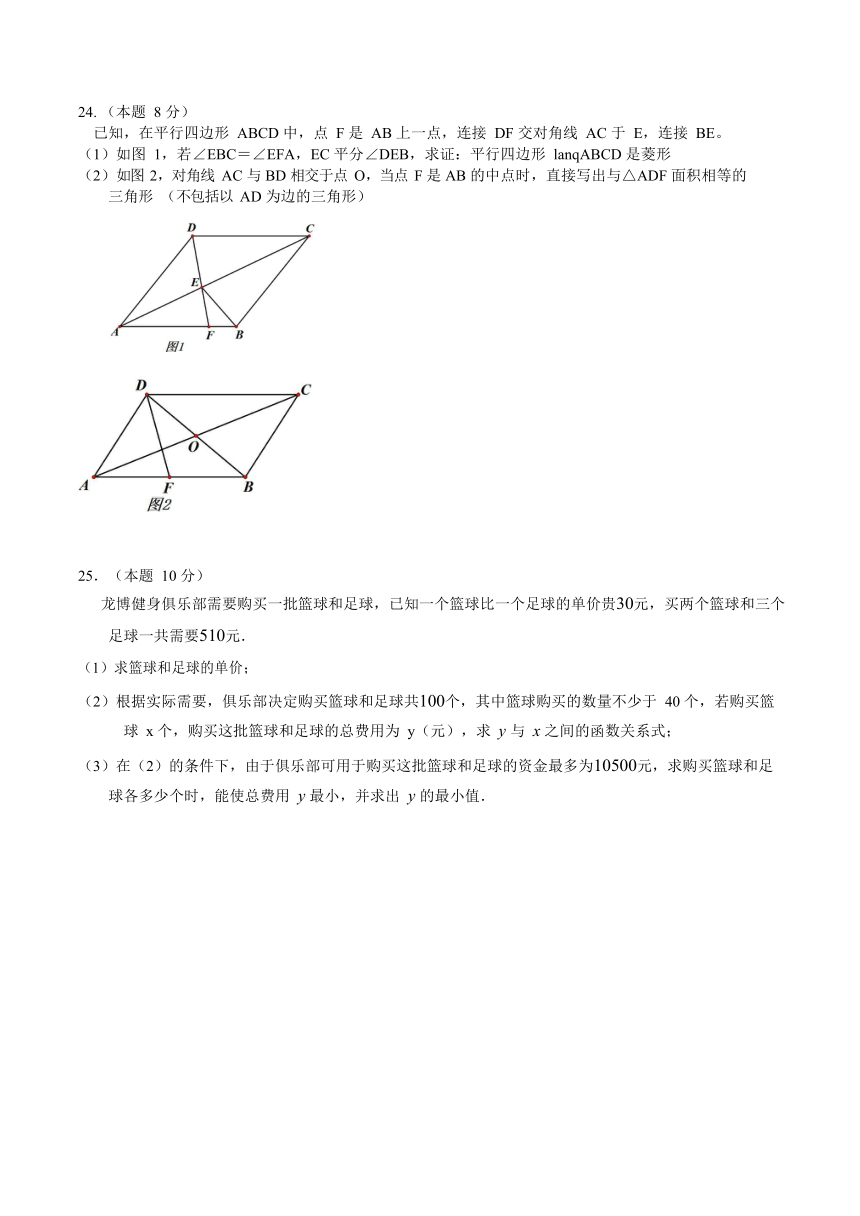
24.
(本题
8
分)
已知,在平行四边形
ABCD
中,点
F
是
AB
上一点,连接
DF
交对角线
AC
于
E,连接
BE。
(1)如图
1,若∠EBC=∠EFA,EC
平分∠DEB,求证:平行四边形
lanqABCD
是菱形
(2)如图
2,对角线
AC
与
BD
相交于点
O,当点
F
是
AB
的中点时,直接写出与△ADF
面积相等的三角形
(不包括以
AD
为边的三角形)
25.(本题
10
分)
龙博健身俱乐部需要购买一批篮球和足球,已知一个篮球比一个足球的单价贵30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,俱乐部决定购买篮球和足球共100个,其中篮球购买的数量不少于
40
个,若购买篮球
x
个,购买这批篮球和足球的总费用为
y(元),求
y
与
x
之间的函数关系式;
(3)在(2)的条件下,由于俱乐部可用于购买这批篮球和足球的资金最多为10500元,求购买篮球和足球各多少个时,能使总费用
y
最小,并求出
y
的最小值.
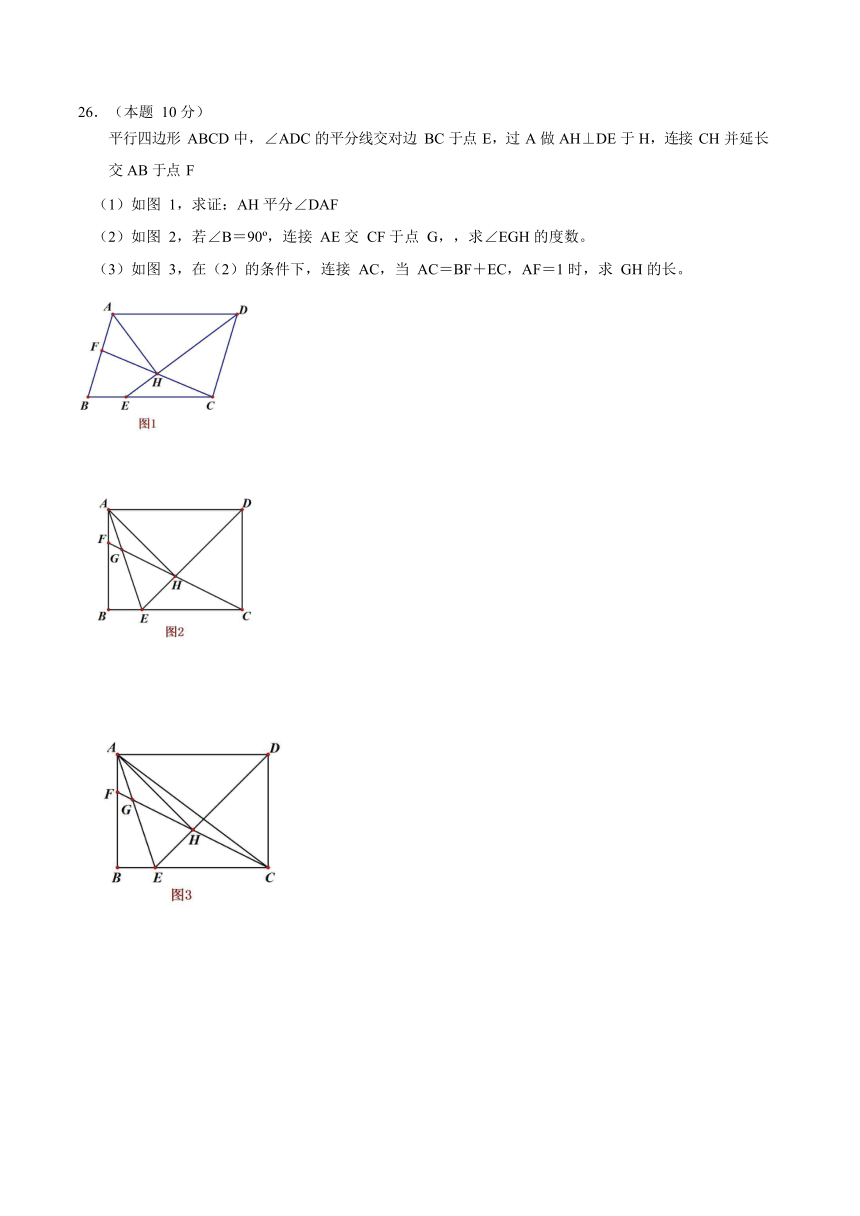
26.(本题
10
分)
平行四边形
ABCD
中,∠ADC
的平分线交对边
BC
于点
E,过
A
做
AH⊥DE
于
H,连接
CH
并延长交
AB
于点
F
(1)如图
1,求证:AH
平分∠DAF
(2)如图
2,若∠B=90?,连接
AE
交
CF
于点
G,,求∠EGH
的度数。
(3)如图
3,在(2)的条件下,连接
AC,当
AC=BF+EC,AF=1
时,求
GH
的长。
27、(本题
10
分)
在平面直角坐标系中,O
为坐标原点,直线
AB
与
y
轴交于点
A,与
x
轴交于点
B,OA=2,△AOB
的面积为
2。
(1)如图
1,求直线
AB
的解析式。
(2)如图
2,线段
OA
上有一点
C,直线
BC
为
y=kx-2k
(
k<0
),AD⊥y
轴,将
BC
绕点
B
顺时针旋转
90?,交
AD
于点
D,求点
D
的坐标,(用含
K
的式子表示)
(3)如图
3,在(2)的条件下,连接
OD,交直线
BC
于点
E,若
3∠ABC-∠BDO=45?,求点
E
的坐标。
答
题
卡
一、选择题
二、填空题
三、解答题
21
、
解(1)
(2)
(
DG
=
)22、
23、
24、
(1)证明:
(2)
25、(1)
(2)
(3)
26、
(
27
、
)
参
考
答
案
题号
1
2
3
4
5
答案
B
C
B
B
C
题号
6
7
8
9
10
答案
B
B
C
A
C
题号
11
12
13
14
15
答案
x≠-1.5
-3
4.8
2
>
题号
16
17
18
19
20
答案
(6,4)
16
4
或
8.5
二题
解答题
解:(1)∵y与x+2成正比例
∴设y=k(X+2)(K≠0)
∵X=4时,y=12
∴k(4+2)=12
∴k=2∴y=2(x+2)=2x+4
当y=24时,24=2x+4
∴x=10
22.
23、(1)50海里
(2)(-1)小时
24、证明:(1)∵四边形ABCD是平行四边形
∴AB∥CD
∴∠CDF=∠AFE
∵∠EBC=∠EFA
∴∠EBC=∠EDF
∵EC平分∠DEB
∴∠DCE=∠BCE
又∵CE=CE
∴△CED≌△CEB
∴CD=CB
∵四边形ABCD为平行四边形
∴平行四边形ABCD为菱形
(2)△AOB、△BOC,△COD,△DFB
(1)A货物120元,B货物90元
(2)y=30x+9000
(3)购买篮球40个,足球60个时,
(1)
(2)
(3)
(1)
y=-x+2
(2)
D(2-2K,2)
E(,)
2019--2020
学年度(下)
八年级五月份质量检测数学试卷
温馨提示:亲爱的同学们,病毒无情,人有情,这份试卷再次记录着你的成长,请相信自己,认真审题,看清要求,仔细答卷。祝你成功!
一、选择题(每题
3
分,共
30
分)
1.下列各图中表示
y
是
x
的函数图像的是(
)
2.下列各组线段中,能构成直角三角形的是(
)
A.2,3,4
B.3,4,6
C.5,12,13
D.
4,6,7
3.如图,四边形
ABCD
为平行四边形,作∠BAD
的平分线,交
DC
边于点
E,
若∠DEA=30°,则∠B
的度数为(
)
A.100°
B.120°
C.135°
D.150°
4.一次函数
y=kx+b
的图象经过第一、三、四象限,则(
)
A.
k>0,b>0
B.
k>0,b<0
C.
k<0,b>0
D.
k<0,b<0
5.下列性质中,矩形具有而一般的平行四边形不具有的特点是(
)
A.对边相等
B.对角相等
C.对角线相等
D.对边平行
6.
若
a
b
c
0
,则一元二次方程
ax2
bx
c
0(a
0)
必有一根是(
)
A.0
B.1
C.
-1
D.
无法确定
7.如图,已知□ABCD
的面积为
48,E
为
AB
的中点,连接
DE,则△ODE
的面积为(
).
A.8
B.6
C.4
D.3
7
题
8
题
9
题
8.如图,矩形
ABCD
中,AB=8,AD=6,折叠纸片,使边
AD
落在对角线
BD
上,点
A
对应点
E,折痕为
DG,则
DG
长为(
)
A.
3
B.5
C.
D.
9.
如图,函数
y=2x
和
y=ax+4
的图象相交于点
A(m,3),则不等式
2x<ax+4
的解集为(
)
A.
x
3
2
B.x<3
C.
x
3
2
D.x>3
10.仁爱药店在“抗疫”期间销售一种消毒液,如果一次购买
10
瓶以上(不含
10
瓶),超过
10
瓶的那部分的价格将打折,并依此得到付款金额
y(单位:元)与一次购买消毒液数量
x(单位:瓶)之间的函数关系如图所示.下列四种说法:其中正确的个数是(
)
①一次购买消毒液数量不超过
10
瓶时,销售价格为
5
元/瓶;
②一次购买
30
瓶时,付款金额为
100
元;
③一次购买
10
瓶以上时,超过
10
瓶的那部分消毒液的价格打七折;
④一次购买
40
瓶消毒液比分两次购买且每次购买
20
瓶消毒液少花
25
元钱.
A.1
B.2
C.3
D.4
二、填空题(每题
3
分,共
30
分)
10
题
x
11.函数
y=
2x
3
中自变量
x
的取值范围是
。
12.当
a
=
时,(a
3)x
a
1
x
5是关于
x
的一元二次方程
。
13.
在
Rt△ABC
中,CD
斜边
AB
上的高,若
AB=10,AC:BC=3:4,则
CD=
.
(
2
)14.如图,四边形
ABCD
中,BD⊥DC
于点
D,∠DCB=45°,∠ABD=∠ECD,点
F
是
BC
的中点,已知
BD=
2
,则
FE
的长是
.
14
题
16
题
17
题
15.已知点(-6,m),(8,n)都在直线
y=-x-b
上,则
m
n。(填大小关系)
16.
如图坐标系,四边形
ABCD
为菱形,顶点
A、B
在
x
轴上,AB=5,点
C
在第一象限,且菱形
ABCD
的面积为
20,
A
坐标为(-2,0),则顶点
C
的坐标为
17.如图,矩形
ABCD
的对角线相交于点
O,OF⊥BC,CE⊥BD,
OE∶BE=1∶3,OF=4,则线段
BD
的长为
.
18.如图,△ABC
中,AD⊥BC
于
D,F
为△ABC
外一点,
连
DF
交
AB
于
E,∠FBD=∠FDA=∠C,FD=AD=4,
BC=8,则△ADE
与△BFE
的面积差为
。
18
题
19.已知菱形
ABCD
的边长为
6,∠A=60°,如果点
P
是菱形
(
3
)内一点,且
PB=PD=2
,那么
AP
的长为
。
20.如图∠BAC=90°,∠ABC=2∠CAD,∠ADE=45°,
9
BE=
2
,CD=1,则
BC=
。
20
题
三、解答题
21.(本题
7
分)
已知
y
与
x+2
成正比例,当
x=4
时,y=12.
(1)求
y
与
x
之间的函数关系.
(2)当
y=24
时,求
x
的值
22.(本题
7
分)
如图,在每个小正方形的边长均为1
的方格纸中有线段AC
和EF,
点
A、C、E、F
均在小正方形的顶点上.
(1)在方格纸中画出一个以
AC
为对角线的菱形
ABCD,点
D
在直线
AC
的下方,且点
B、D
都在小正方形的顶点上;
(2)在方格纸中画出以
EF
为底边,面积为
6
的等腰三角形
EFG
且点
G
在小正方形的顶点上;
(3)在(1)、(2)的条件下,连接
DG,请直接写出线段
DG
的长.
23.(本题
8
分)
如图,已知射线
MN
表示一艘轮船的航行路线,从
M
到
N
的走向为南偏东
30°,在
M
的南偏东
60°
方向上有一灯塔
A,灯塔
A
到
M
处的距离为
100
海里.
(1)求灯塔
A
到航线
MN
的距离;
(2)在航线
MN
上有一点
B,且∠MAB=15°,若轮船的航速为
50
海里/时,求轮船从
M
到
B
处所用的时间为多少小时?
(结果保留根号)
(第
23
题图)
24.
(本题
8
分)
已知,在平行四边形
ABCD
中,点
F
是
AB
上一点,连接
DF
交对角线
AC
于
E,连接
BE。
(1)如图
1,若∠EBC=∠EFA,EC
平分∠DEB,求证:平行四边形
lanqABCD
是菱形
(2)如图
2,对角线
AC
与
BD
相交于点
O,当点
F
是
AB
的中点时,直接写出与△ADF
面积相等的三角形
(不包括以
AD
为边的三角形)
25.(本题
10
分)
龙博健身俱乐部需要购买一批篮球和足球,已知一个篮球比一个足球的单价贵30元,买两个篮球和三个足球一共需要510元.
(1)求篮球和足球的单价;
(2)根据实际需要,俱乐部决定购买篮球和足球共100个,其中篮球购买的数量不少于
40
个,若购买篮球
x
个,购买这批篮球和足球的总费用为
y(元),求
y
与
x
之间的函数关系式;
(3)在(2)的条件下,由于俱乐部可用于购买这批篮球和足球的资金最多为10500元,求购买篮球和足球各多少个时,能使总费用
y
最小,并求出
y
的最小值.
26.(本题
10
分)
平行四边形
ABCD
中,∠ADC
的平分线交对边
BC
于点
E,过
A
做
AH⊥DE
于
H,连接
CH
并延长交
AB
于点
F
(1)如图
1,求证:AH
平分∠DAF
(2)如图
2,若∠B=90?,连接
AE
交
CF
于点
G,,求∠EGH
的度数。
(3)如图
3,在(2)的条件下,连接
AC,当
AC=BF+EC,AF=1
时,求
GH
的长。
27、(本题
10
分)
在平面直角坐标系中,O
为坐标原点,直线
AB
与
y
轴交于点
A,与
x
轴交于点
B,OA=2,△AOB
的面积为
2。
(1)如图
1,求直线
AB
的解析式。
(2)如图
2,线段
OA
上有一点
C,直线
BC
为
y=kx-2k
(
k<0
),AD⊥y
轴,将
BC
绕点
B
顺时针旋转
90?,交
AD
于点
D,求点
D
的坐标,(用含
K
的式子表示)
(3)如图
3,在(2)的条件下,连接
OD,交直线
BC
于点
E,若
3∠ABC-∠BDO=45?,求点
E
的坐标。
答
题
卡
一、选择题
二、填空题
三、解答题
21
、
解(1)
(2)
(
DG
=
)22、
23、
24、
(1)证明:
(2)
25、(1)
(2)
(3)
26、
(
27
、
)
参
考
答
案
题号
1
2
3
4
5
答案
B
C
B
B
C
题号
6
7
8
9
10
答案
B
B
C
A
C
题号
11
12
13
14
15
答案
x≠-1.5
-3
4.8
2
>
题号
16
17
18
19
20
答案
(6,4)
16
4
或
8.5
二题
解答题
解:(1)∵y与x+2成正比例
∴设y=k(X+2)(K≠0)
∵X=4时,y=12
∴k(4+2)=12
∴k=2∴y=2(x+2)=2x+4
当y=24时,24=2x+4
∴x=10
22.
23、(1)50海里
(2)(-1)小时
24、证明:(1)∵四边形ABCD是平行四边形
∴AB∥CD
∴∠CDF=∠AFE
∵∠EBC=∠EFA
∴∠EBC=∠EDF
∵EC平分∠DEB
∴∠DCE=∠BCE
又∵CE=CE
∴△CED≌△CEB
∴CD=CB
∵四边形ABCD为平行四边形
∴平行四边形ABCD为菱形
(2)△AOB、△BOC,△COD,△DFB
(1)A货物120元,B货物90元
(2)y=30x+9000
(3)购买篮球40个,足球60个时,
(1)
(2)
(3)
(1)
y=-x+2
(2)
D(2-2K,2)
E(,)
同课章节目录
